Dört Renk Problemi

_{Yazar: Ayşe Berkman, Ali Doğanaksoy, Ebru Keyman}

Bir haritanın renklendirilmesinde, birbirine komşu iki bölgenin farklı renklerde olması koşuluyla en az kaç renk kullanmak gerekir? Bazı küçük veya özel haritalar için bu soruya cevap vermek kolay olabilir. Örneğin, satranç tahtasına benzer bir haritayı boyamak için iki renk yeterli olacaktır. Çok karmaşık bir haritada ise sorunun cevabını deneme yaparak bulmak çok zor olabilir. Sözgelimi, 10 bölgesi olan bir haritanın 4 renk kullanarak 1048576 farklı şekilde renklendirilebileceği düşünülürse, deneme yoluyla araştırma yapmanın güçlüğü anlaşılır. Acaba yeterli renk sayısı için, en karmaşık bir haritada bile her zaman emin olabileceğimiz bir alt sınır var mıdır? 1852’de ortaya atılan bu problem 1976’da çözülmüş ve gösterilmiştir ki, en karmaşık bir harita dahi dört renkle boyanabilir.

Bir haritanın boyanması için dört rengin yeterli olacağını ilk sezinleyen belki de Francis Guthrie idi. 1852 yılında kardeşi Frederick’e yazdığı mektupta bu beklentisinden söz ediyor ve bunun matematik ispatının nasıl olabileceğini soruyordu. Soruya cevap bulamayan Frederick de problemi hocası olan matematikçi Augustus De Morgan’a götürüyordu. Ancak De Morgan da böyle bir ispatın olup olmadığını bilmiyordu. Böylece dört renk problemi olarak ünlenen ve şu iki önermenin gerçeklenmesini isteyen problem ortaya çıktı:

1. Renklendirilebilmesi için en az dört renk gerektiren haritalar vardır.
2. Renklendirilebilmesi için beşinci renk gerektiren harita çizilemez.

İlk önermeyi gerçeklemek De Morgan İçin kolay oldu. Her biri diğer üçüne komşu olan dört ülkenin yer aldığı bir haritanın boyanması için elbette en az dört renge ihtiyaç vardı. Bu tür haritaların varlığını göstermek de zor değildi. Aşağıdaki şekilde böyle bir haritanın bir bölümü yer almaktadır. O halde birinci önerme doğrudur.

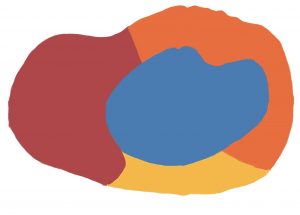
De Morgan benzer şekilde, her biri diğer dördüne komşu olan beş ülkenin yer aldığı bir haritanın olup olmadığını incelemeye başladı. Böyle bir harita olsaydı, dört renk problemi olumsuz olarak çözülmüş olacaktı. Ancak, De Morgan şunu gösterdi: Düzlemde (veya küre üzerinde) çizilmiş bir haritanın hiçbir kısmında hepsi birbirine komşu olan beş ülke yer alamaz. İlk bakışta bu ispat yukarıdaki ikinci soruya bir cevap gibi görülebilir. Ancak, birbirine komşu beş ülkenin bulunmaması, haritanın boyanması için beş renk gerektirmesini engellemez. Bunu bir örnekle şöyle gösterebiliriz. Aşağıdaki haritada birbirine komşu olacak şekilde dört ülke yer almamaktadır. Ancak bu harita yine de en az dört renkle boyanabilir.

Bu soruyu çözmeye çalışan ancak ispatını yapamayan Arthur Cayley, 1878 yılında problemi Londra Matematik Cemiyeti’ne sundu. Artık problem geniş bir kitlenin ilgisine sunulmuştu ve bir asıra yakın bir süre bir çok amatör ve profesyonel matematikçinin ilgisini üzerinde toplayacaktı.

Problemin sunuluşunun üzerinden bir sene bile geçmeden Alfred Bray Kempe, geliştirdiği bir yöntemi gündeme getirdi. Bu yöntemle problem tam olarak çözülmemişti. Ancak, dört-renk problemiyle uğraşanların en çok baş vurdukları yol olmuştu.

Şimdi, Kempe’nin bu yöntemini adım adım izleyelim.

A. Hiçbir bölgesi bir veya daha fazla bölgeyi tamamen çevrelemeyen bir haritaya normal harita; her köşesinde tam üç sınır çizgisi buluşan bir normal haritaya da üçüncü dereceden normal harita denir.

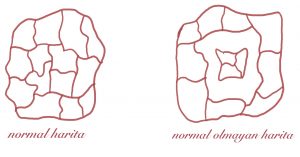
B. Renklendirilebilmesi için beş renk gerektiren bir harita varsa, buna bağlı olarak, aynı özellikte bir normal harita vardır. Ya da, beşinci renk gerektiren normal harita yoksa, beşinci renk gerektiren genel bir harita da yoktur. Bu nedenle incelemeyi normal haritalarla sınırlı tutmak yeterlidir.

C. Beş renk gerektiren normal haritalar olduğunu kabul edelim. Bunların içinde ülke sayısı en az olanlara da beş renk gerektirir minimal haritalar (ya da kısaca minimal haritalar) diyelim. Eğer minimal haritaların olmadığı gösterilebilirse, buna bağlı olarak, beş renk gerektirir normal harita olmadığı da ispatlanmış olur. Şimdi minimal haritaların var olduğunu kabul edelim ve böyle bir haritanın ülke sayısını da \(N\) ile gösterelim. Bu halde, ülke sayısı \(N\)-den az olan her harita dört renkle boyanabilir. Veya, bir harita en az beş renkle boyanabiliyorsa en az \(N\) ülkesi vardır.

D. Bir normal haritada ülkelerin tümü birden altı veya daha fazla komşuya sahip olamaz. Bir başka deyişle, bir normal haritada iki, üç, dört veya beş komşusu olan en az bir bölge vardır. O halde, bir normal haritada aşağıdaki şekillerden en az bir tanesinin yer alması kaçınılmazdır.

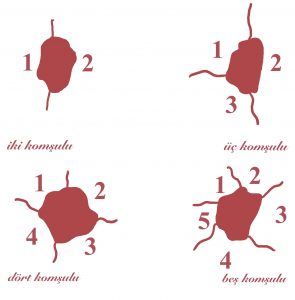
Bu nedenle, bu dört şekilden oluşan kümeye Kempe kaçınılmaz kümesi denir.

E. \(N\)-bölgeli bir normal haritada iki komşusu bulunan bir ülke olduğunu varsayalım. Bu ülke, komşu ülkelerden biriyle birleşirse elimizde \(N – 1\) bölgeli bir harita olur ki, bunu da dört renkle boyayabiliriz. Demin komşusu ile birleşen ülkeyi yeniden haritaya ekleyelim. Bu durumda biri hariç, bütün ülkeleri istenen şekilde dört renk kullanarak boyanmış bir harita elde ederiz. Boyanması gereken ülkenin ise yalnızca iki komşusu vardır. O halde bunu da komşularından farklı ama haritada kullanılmış renklerden biriyle boyayabiliriz. Şonuçta dört renkle boyanmış bir harita ortaya çıkar ki, bu da bir minimal haritanın sadece iki komşusu olan bir ülkesi olamayacağını gösterir. Aynı şekilde, \(N\)- bölgeli bir normal haritada üç komşusu bulunan bir ülke olduğunu farzedelim. Bu ülke, komşu ülkelerden biriyle birleşsin. Bu durumda, ortaya çıkan \(N – 1\) bölgeli haritayı dört renkle boyayabiliriz. Bu ülkeyi yeniden haritaya ekleyerek yine, biri hariç, bütün ülkeleri istenen şekilde dört renk kullanarak boyanmış bir harita elde ederiz. Boyanması gereken ülkenin ise yalnızca üç komşusu vardır. Bu komşular da birbirleri ile komşu olduğundan her biri farklı renktedir. Boyanması gereken ülkeyi haritada kullanılan diğer renklerden biriyle boyarsak, dört renkle boyanmış \(N\) ülkeli bir harita ortaya çıkar ki, bu da minimal bir haritanın sadece üç komşusu olan bir ülkesi de olamayacağını gösterir. Biraz daha karmaşık olmakla birlikte, benzer akıl yürütmelerle gösterilebilir ki, içinde sadece dört komşulu bir ülke bulunan, \(N\) bölgeli bir normal harita da dört renkle boyanabilir. Eğer, sadece beş komşusu bulunan bir ülkeye sahip, \(N\) ülkeli normal haritanın da dört renkle boyanabileceğini gösterebilseydik, problemi çözmüş olacaktık.

Kempe de bir normal haritada beş komşulu bir ülke olması halinde renklendirmenin dört renkle yapılabileceğini gösteren bir ispat verdi. Fakat kısa zaman sonra bu ispatın yanlış olduğu gösterildi.

Kempe’nin metodundaki temel şudur: Elemanları olan şekillerden en az birisinin her normal haritada yer alması gereken kümelere kaçınılmaz küme denir. ‘Kempe kaçınılmaz kümesi’ de buna bir örnektir. Belli bir şekil, \(N\) ülkeli normal bir haritada yer aldığı zaman, o haritanın dört renkle boyanabileceği gösterilebiliyorsa, bu şekile de indirgenebilir şekil denir. Örneğin, sadece iki komşusu bulunan bir ülke, indirgenebilir şekildir. O halde, dört renk probleminin olumlu çözümü için, bütün elemanları indirgenebilir olan bir kaçınılmaz küme bulunmalıdır.

Bu metodla problemi çözmeye çalışanların karşılaştığı en büyük zorluk şuydu: Ya kaçınılmaz kümenin eleman sayısı çok büyük oluyordu ya da kaçınılmaz kümede yer alan şekillerin indirgenir olup olmadığını incelemek uzun vakit alıyordu. Her iki halde de, problemin çözümü için sabırla ve belki de yıllarca tek tek yüzbinlerce olasılığın değerlendirilmesi gerekiyordu.

Bilgisayarların ortaya çıkışı ile problem üzerinde çalışanlar, ellerindeki şekillerin incelenmesini bu hızlı araçlara yaptırmaya başladılar. Yine de çok uzun süre gerekiyordu. Örneğin, Appel ve Haken, 1970’de elde ettikleri kaçınılmaz kümenin bütün elemanlarının incelenmesinin, o zamanki bilgisayarların hızı ile, \(4^4 \times 10^3 \times 25\) dakika (12 sene 2 aydan biraz fazla) süreceğini hesaplamışlardı.

Zamanla, bilgisayarlar daha büyük hıza erişiyor ve problemle uğraşanlar da yeni teknikler geliştiriyordu. Nihayet, 1976 yılında, Appel ve Haken 1482 şekilden oluşan bir kaçınılmaz kümenin bütün elemanlarının indirgenebilir olduğunu gösterdiler. Bu iş için toplam 1200 saat bilgisayar kullanmak gerekmişti.

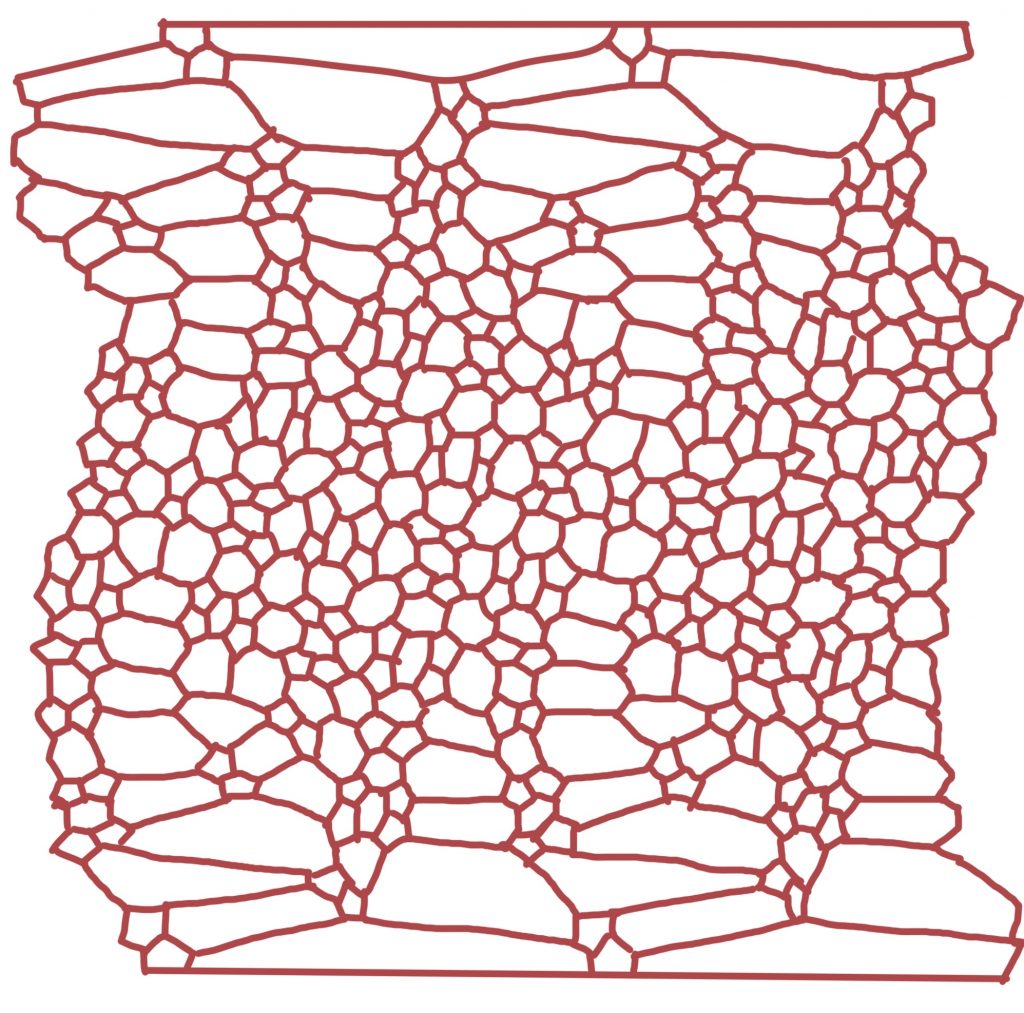
Artık, her haritanın dört renkle boyanabileceğini biliyoruz. Ancak bunun nasıl yapılabileceğini bilmiyoruz. Öyle karmaşık haritalar çizilebilir ki, dört renkle boyanabileceğini bilmemize karşın, haritayı boyamakta güçlük çekebiliriz. Böyle bir harita yazının sonunda, okuyucunun denemesi için verilmiştir.

Herhangi bir harita dört renkle boyanabilir. Bunu kesinlikle biliyoruz. Ancak, yine biliyoruz ki, bazı haritaları boyamak için daha az renk yeterli olabilir. Bir haritanın iki veya üç renkle boyanması için verilen kriterler şunlardır:

• Bir haritanın iki renkle boyanabilmesi için gerek ve yeter koşul haritanın tüm köşelerinde çift sayıda sınır çizgisinin buluşmasıdır.
• Bir haritanın üç renkle boyanabilmesi için gerek ve yeter koşul her ülkenin çift sayıda komşusu olmasıdır.

Bütün bu söylediklerimize rağmen, dünya haritası veya Türkiye haritası gibi haritaları dört renkle boyamak mümkün olmayabilir. Çünkü, böyle haritalarda uyulması gereken kurallar vardır. Söz gelimi, bütün göller ve denizler maviye boyanmalıdır. Böyle zorlayıcı kurallar, haritanın boyanması için gerekli renk sayısını fazlalaştırabilir. Ancak, hiçbir zorlayıcı koşul yoksa, her haritayı komşu ülkeler farklı renklerde olmak üzere sadece dört renk kullanarak boyayabiliriz.

Dört renk teoreminin ispatı düzleme (veya küre yüzeyine) çizilen haritalar için yapılmıştır. Farklı yüzeylerde, renk sayısı için farklı alt sınırlar verilebilir. Örneğin, torus (simit biçimindeki yüzey) için bu alt sınır 7’dir. Aşağıdaki harita, komşu ülkeler farklı renklerde olmak üzere sadece dört renk kullanarak boyanabilir.
Deneyiniz.

KAYNAKLAR

1. Oystein Ore, Graphs and their uses. Second edition. Edited and with an introduction by Robin J. Wilson. Mathematical Association of America, 1990. 
2. Kenneth Appel, Wolfgang Haken, The Solution of the Four-Color-Map Problem, Scientific American, sayı 237, sayfa 108-121, Ekim 1977.

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

Ayşe Berkman’dan 15.08.2021 tarihinde gelen mesaj:
Aslında bu çalışmayı ilk olarak, Mayıs 1990’da ODTÜ Matematik Bölümü’nde düzenlenen “Matematik Haftası” etkinlikleri çerçevesinde bölümdeki panolarda sergilenmek üzere, sınıf arkadaşım Ebru ile birlikte hazırlamıştık. Ancak o sırada epey deneyimsiz olduğumuz için (lisans ikinci sınıf öğrencisiydik) şimdi fark ediyorum ki, kullandığımız kaynaklara yazıda yer vermemişiz (hatırladığım kaynaklar web sayfasına eklendi) ve bizi yönlendiren ve her aşamada yardım eden Alev Topuzoğlu hocamıza teşekkür etmemişiz (geç de olsa, çok teşekkürler Alev hocam). Daha sonra MD’nin ilk editörü olan Cemal Koç hocamız bizden köşede yazdıklarımızı dergi için yeniden düzenlememizi istedi, o sırada Yayın Kurulu’nda olan Ali hoca da yazının düzenlenmesine yardım etti. Böylece bu yazı ortaya çıktı.