İsmail Güloğlu
N'oldu bu gönlüm, n'oldu bu gönlüm Derd ü gamınla doldu bu gönlüm
– Bugün bir açıyı ikiye bölmeyi öğrendik.
– Şu halde dörde, sekize, onaltıya,… bölmeyi de biliyorsun artık.
– Evet
– Peki bütün bu bölmeleri sağlayan ana işlem yani “açıyı ikiye bölme” nasıl gerçekleştiriliyor? -Tahtada anlatayım…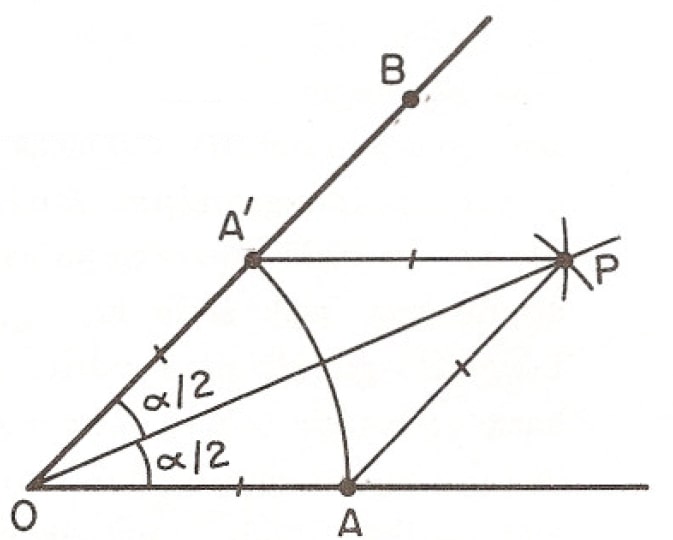
Ölçüsü \(\alpha\) olan açı \(A, O, B\) noktaları ile şekildeki gibi verilmiş olsun. \(O\) merkezli \(|OA|\) yarıçaplı çemberin açının kenarlarını kestiği noktalar sırasıyla \(A\) ve \(A’\) olsun. \(A\) ve \(A’\) merkezli \(|OA|\) yarıçaplı çemberleri çizelim. Bunlar \(O\) ve \(P\) noktalarında kesişirler. \(OP\) doğrusu \(\measuredangle AOB\) açısını ikiye boler, çünkü \(OPA’\) ve \(OPA\) üçgenleri eştirler.
– Fakat niçin bu kadar zahmet çekiyorsun? İletki ile verilen açıyı ölçüp yarısını yine iletki ile çizemez miyim? Burda ölçü hataları çizimin kaçınılmaz hatalarından daha fazla mı oluyor ki?
– Ben soruyu eksik ilettim, galiba. Konumuz bir açıyı gündelik gereksinmelere yanıt verebilen bir yöntemle yaklaşık ikiye bölmek değil, idealize edilmiş araçlarla tam ve kesin olarak ikiye bölmek; üstelik bu bölme işleminde araç olarak sadece cetvel ve pergel kullanmak. Problemi ilginç yapan da bir bakıma bu kısıtlamalar. Bu, doğal olarak araçlarımızın bazı çizimler için yetersiz kalmaları sonucunu doğurabilir. Nitekim sizin yönteminizle bir açı istenildiği kadar sayıda eşit parçaya ayrılabilir, bu arada üç eşit parcaya da, fakat öğretmenimizin söylediğine göre bir açıyı sadece cetvel ve pergel kullanarak üç eşit parçaya ayırmak olanaksızmış.
– Yani öğretmeniniz ve onun bu problemle uğraşan tanıdıkları şimdiye kadar bir açıyı üçe bölmeyi başaramamışlar, bu uyuyan güzeli uyandıracak kudretli prens hâlâ bekleniyor, öyle mi?
– Hayır, yanlış anlamadıysam, öğretmenimizin bahsettiği bir becerememişlik itirafı değil, gerçek bir imkânsızlık iddiası. Problemin büyük gayretlere rağmen henüz çözülemediğini söylemiyor, fakat bir anlamda olumsuz şekilde çözüyor: “İstenen koşulları sağlayan bir çözüm yoktur, çünkü …” deyip bu önermesini kanıtlıyor. “Bütün kenarları ve bir yüksekliği eşit uzunlukta bir üçgen çizmek” problemi gibi. Böyle bir üçgenin hangi araçlarla olursa olsun düzlemde çizilmesi olanaksızdır, çünkü böyle bir üçgen yoktur, deyip bunu kanıtlamakla problem çözülmüş olur. Bunun gibi, bir açıyı sadece cetvel ve pergel kullanarak üç eşit parçaya bölmenin olanaksız olduğu kanıtlanmış sanıyorum.
– Fakat, nasıl olur? Ben bir dik açıyı veya dik açının yarısını veya bunun yarısını,… yani sonsuz tane farklı açıyı sadece cetvel ve pergel kullanarak üçe ayırabilirim.
– Fakat siz, burada özel bir takım açıların üçe bölünmesinden, dolayısıyla ölçüsü ile verilen bazı açıların sadece cetvel ve pergel kullanarak çizilebilmesinden söz ediyorsunuz. Bu kendi başına ilginç olmakla beraber bizim problemimiz değil. Sadece cetvel ve pergel kullanarak, açıyı ikiye bölme çiziminde olduğu gibi, herhangi bir açıya uygulandığında onu üç eşit parçaya ayıran bir çizim metodu veriyor değilsiniz.
– Her açı için uygulanabilir bir algoritma bulunmasa bile her açı kendisine özgü yöntemlerle sadece cetvel ve pergel kullanarak üçe ayrılabilir, olamaz mı?
– Uyarınızı anlıyorum. Belki de öğretmenimizin demek istediği şu idi: “Düzlemde sadece cetvel ve pergel kullanarak üç eşit parçaya ayrılamayan en az bir (dolayısı ile sonsuz tane) açı vardır”. Buna ne dersiniz?
– Şimdi istenen kesinliğe ve açıklığa kavuştuk herhalde, derim. Peki sen ne dersin, hocanın bu iddiası doğru mu?
– Eh, öğretmenimiz bizi kandıracak değil ya. Elbette doğrudur, ben inanıyorum.
– Oğretmenine inanıp güvenmen çok saygı duyulması gereken bir tavır, aranızda böyle bir münasebetin oluşmuş olması bizi ancak sevindirir. Fakat ona olan güveninin onun ağzından çıktı diye matematiksel bir iddiaya “inanmaya” kadar varması, “acaba bir zihnî tembellik mi söz konusu?” diye sorduruyor. İnanç, konusu olan mesajın bellenip kavranıldıktan sonra gerçekliğinin tasdik veya red edilmesi olayıdır. Bu ise insanın o konuyla ilgili melekelerini sonuna kadar harekete geçirerek meseleyle haşır neşir olmasını gerektirir. Yani dinamik bir oluşumdur. Yoksa, inanmak, bu çok yönlü çabanın meşakkatinden kaçmanın bir yolu değildir. İman, “Babalarımızı böyle yapar bulduk” taklitçiliği ile, muhtevasının canlılığını kaybetmeden yaşayamaz. O, hissî, fikrî ve diğer melekelerimizle denenmiş, gerçeklenmiş, yaşanmış olmaya, yani tahkike ihtiyaç duyar. Üstelik matematiksel gerçekliklerin yalın dünyasında bu doğrulama işi bir bakıma çok kolaylaştırılmıştır. Çünkü baştan, incelenen matematiksel nesneler bir aksiyom sistemi ile kapalı olarak da olsa kesin bir şekilde tanımlanmışlardır. Ve bunlar hakkında doğrulara ulaşma verilen aksiyom sisteminden hareketle yapılacak mantıksal çıkarımlara indirgenmiştir. Bunların kuralları da her türlü şüpheden ve kaypaklıktan arındırılmış, açık seçik hale getirilmiştir. Böylelikle gerekli zihnî çabayı harcamaya hazır herkes için tam ve kesin matematiksel bilgiye ulaşmak mümkündür. Böyle iken, bir matematiksel iddiayı, ispat ederek veya hiç olmazsa yapılmış ispatları ciddiyetle takip ederek gerçekleme yoluna gitmeyip kolaya kaçarak “inandım” denmesi, sadece insanın taklit seviyesinde kalmasına neden olmuyor, fakat ispat denen yoğun ve yönlenmiş zihnî çabanın getirdiği, uğraşılan problemi derinlemesine anlama ve bu çabayla oluşma imkanının da yitirilmesine neden oluyor.
– Fakat bir problemin çözümü, bu çözümü kavrayacak zihnî olgunluğa, bilgi birikimine varmadan pek mümkün olamaz herhalde. Ben hiçbir lise matematik kitabında açının üçe bölünmesi probleminin tartışıldığını görmedim. Konu bizim bilgi ve deneyimlerimizi aşıyor sanırım.
– Zihnî olgunluk ve fikrî birikim zamanın geçmesi ile kendiliğinden oluşmaz. Bize verilenleri yerli yerince kullanmamız, emek vermemiz, çile çekmemizle doğar, gelişir. Mesela, şimdi bu açıyı üçe bölme problemi ile karşılaşmış, ilgimiz buna çekilmiş, aklımız, fikrimiz buna meyletmiş iken, sınırlarımıza ulaşıncaya kadar üzerinde düşünmezsek ayıp etmiş olmaz mıyız? Zaten bilgi ve becerimizin neye yetip, neye yetmeyeceğini bize başkaları söyleyecek değil; böylesi bir sınır da yok. Bize düşen günlük kaygulardan soyutlanıp sebat ve azimle sorunların üzerine gitmek, yaşam içinde çalışıp kendimizi bulmak, anlamak ve oluşturmaktır.
– Peki, bu işe, bu problemle ilgili olarak nerden başlayalım?
– İstersen önce şu çizim metodu üzerinde konuşalım:
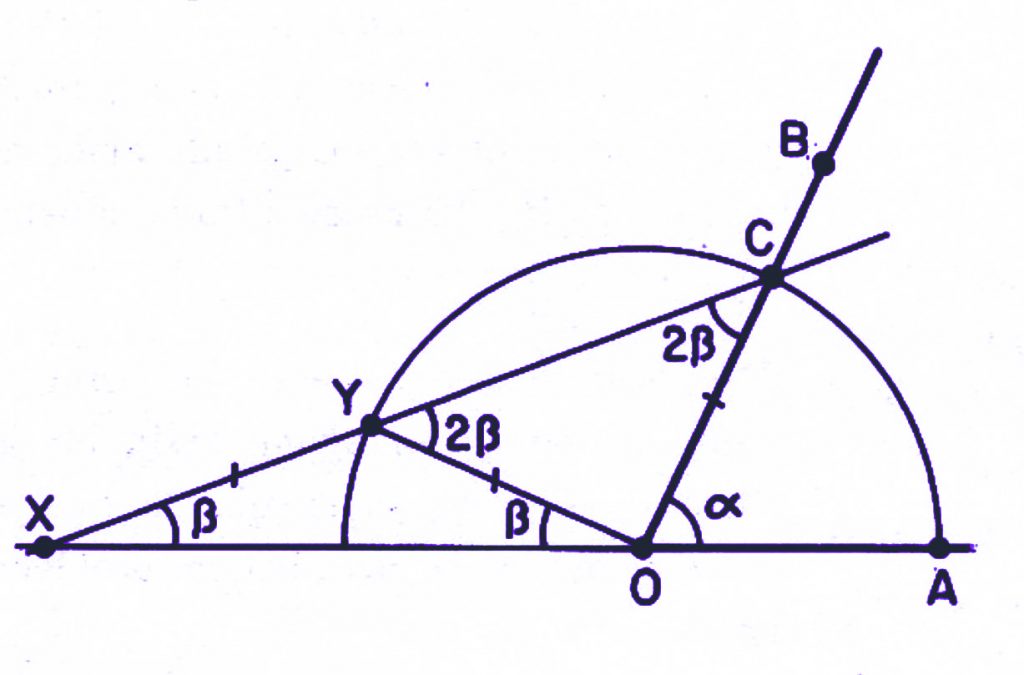
Şekildeki gibi \(A, O, B\) noktaları ile bir \(\alpha\) dar açısı verilmiş olsun. \(O\) merkezli \(|OA|\) yarıçaplı çemberin \(OB\) ışınını kestiği nokta \(C\) olsun. Bir cetvel üzerinde aralarındaki uzaklık \(|OA|\)’ya eşit olan iki nokta, \(X\) ve \(Y\) işaretliyelim ve cetveli \(X\) noktası \(OA\) doğrusu üzerinde kalmak ve cetvel \(C\) noktasından geçmek şartıyla öyle hareket ettirelim ki \(Y\) noktası \(O\) merkezli \(|OA|\) yarıçaplı çember üzerine gelsin. Bu konumda \(\measuredangle AXC\) açısının ölçüsü \(\frac 1 3 \alpha\) dır.
– Gerçekten \(\Delta XYO\) ve \(\Delta COY\) üçgenleri ikizkenar üçgenler olduğu için \(\measuredangle AXC = \beta\) dersek \(\alpha + \beta = 180^\circ – (180^\circ – 4 / \beta) = 4 \beta\) yani \(3 \beta = \alpha\) olduğu görülüyor.
– \(\alpha\) herhangi bir dar açı olmak üzere \(\frac{\alpha} 3\) açısını sadece cetvel ve pergel kullanarak çizmiş olmadık mı?
– Beni şaşırtıyorsunuz!
– Ben değil, olsa olsa alışkanlıklarımızın oluşturduğu düşünce kalıpları seni şaşırtmış olabilir. Öğretmeninizin iddiasının doğru olduğu düşüncesini hâlâ sürdüreceksek bu çizimde “sadece cetvel ve pergel” kullanmanın getirdiği kısıtlamalara uymadığımız hükmüne varmamız lazım.
– Biz cetveli sadece doğruları çizmekte değil, uzunlukları ölçmek için de kullanıyoruz. Siz de bu çizimde ölçme denebilecek, ölçülmüş bir uzunluğu cetvele uygun bir konuma yerleştirmek gibi bir işlem yaptınız, “işaretli bir cetvel” kullandınız. Herhalde izin verilmeyen işlem bu oldu.
– Evet, benim de bildiğim “cetvel” işaretsiz, sadece tek kenarı kullanılabilir, istenildiği kadar uzun, herhangi verilmiş iki noktanın belirlediği doğruyu çizmek için kullamlan bir araç. Pergel ise verilmiş bir noktayı merkez olarak kabul eden ve yarıçapı verilmiş iki nokta arasındaki uzaklığa eşit olan çemberi çizen araç.
– “Verilmiş nokta”dan kastınız ne? Çizimin yapılacağı düzlemle birlikte bu düzlemin her noktası da verilmiş olmaz mı?
– Her matematiksel iddia “verilen” bir hipotez ile bunun doğru olması halinde, “varılan” bir hükümden oluşur. Her geometrik çizim de, meselâ, bir üçgenin çevrel çemberinin, veya bir elipse dışındaki bir noktadan teğetlerin çizilmesi problemlerinde olduğu gibi bir takım “verilen” noktalar, doğrular, geometrik şekillerden (üçgen; elips ve dışında bir nokta) hareket eder. Biraz dikkatle incelenirse bütün çizim problemlerinde (bizimkinde aşikâr olarak) aslında sonlu tane nokta verilmektedir (üçgende üç köşe noktası, çemberde merkez ve üzerindeki bir nokta, elipsde doğrultman doğrusunu belirleyen iki nokta ile bir odak noktası, v.s. gibi), ve yine sonlu tane noktanın çizilmesi ile tamamen belirlenen geometrik nesnelere ulaşılmak istenmektedir. Yani bir geometrik çizim problemi “verilen” sonlu sayıda noktadan hareketle ve belirli araçlar kullanılarak, verilen noktalarla problemin istediği şekilde bağlantılı sonlu sayıda “amaç” noktayı çizmek meselesidir. Burda çizilmek demek izin verilen yöntemlerle gerçekleştirilen iki ayrı geometrik yerin arakesiti olarak verilebilmek demektir. Şuna dikkat etmek lâzım: Meselâ, merkezi ve bir noktası ile bir çember tamamen belirlenmiş olur. Fakat bu iki nokta ile çemberin bir geometrik yer olarak tamamen belirli olması ile üzerindeki her nokta da “verilmiş” noktalar olmaz. Bunun bir noktasının verilmiş olması, onun adının konabilmesi, çemberin diğer noktalarından ayırd edici bir özelliğinin bilinmesi, demektir. Bizim problemimizde \(O\) köşeli \(\measuredangle AOB\) açısı \(A, O, B\) noktaları ile verildi ise, bu noktalarla \(O\) merkezli \(|OA|\) yarıçaplı çemberin her noktasının da “verilmiş” olması demek olsaydı, çemberin \(\measuredangle AOC = \frac 1 3 \measuredangle AOB\) şartı ile tek türlü ve tamamen belirli \(C\) noktası da “verilmiş” olur ve böylece \(OC\) doğrusu çizilebilir ve açıyı üçe bölmek diye bir problem olmazdı.
– Fakat herhalde “verilmiş” noktalar başlangıç noktalarından ibaret değil. Çizimin bu adımıyla elde edilen yeni noktalar da bunlara ekleniyor. Yani “verilen noktalar” çizim boyunca bir cins evrimleşerek amaç noktalara ulaşıyorlar.
– Veya ulaşamıyorlar.
– Şöyle diyebiliriz galiba: \(\mathcal{P}\) bir düzlemin bazı noktalarından oluşan bir küme olsun. Bir doğruya, \(\mathcal{P}\)’deki farklı iki noktadan geçiyorsa “\(\mathcal{P}\)’ye göre çizilebilir” bir doğru, ve bir çembere, merkezi \(\mathcal{P}\)’deki bir nokta ve yarıçapı \(\mathcal{P}\)’deki iki nokta arasındaki uzaklığa eşit ise “\(\mathcal{P}\)’ye göre çizilebilir” bir çember diyelim. \(\mathcal{P}\) kümesine göre çizilebilir bütün doğrular ile \(\mathcal{P}\) kümesine göre çizilebilir bütün çemberlerin bütün mümkün kesişim noktalarına \(\mathcal{P}\) kümesine göre bir adımda çizilebilir noktalar diyelim ve bunların kümesini \(\mathcal{P}’\) ile gösterelim. Şimdi \(\mathcal{P}_0\) sonlu bir başlangıç noktaları kümesi olmak üzere tümevarımla, \(\mathcal{P}_n, n \in \mathbb{N}\) kümelerini, \(\mathcal{P}_1 = \mathcal{P}_0 \cup \mathcal{P}_0’\) ve \(i \in \mathbb{N}\) için \(\mathcal{P}_i\) tanımlandı ise \(\mathcal{P}_{i + 1} := \mathcal{P}_i \cup \mathcal{P}_i’\) olacak şekilde tanımlayalım. Buna göre \(\mathcal{P}_0\) dan başlayarak sadece cetvel ve pergel kullanarak çizilebilecek noktalar \(C(\mathcal{P}_0) = \cup_{n = 0}^\infty \mathcal{P}_n\) kümesini oluştururlar. Yani \(\mathcal{P}_0\)dan başlayarak bizim araçlarımızla bir geometrik çizimin yapılabilmesi bu çizimin amaç noktalarının \(C(\mathcal{P}_0)\) kümesine ait olması demektir.
– Çok güzel, cetvel ve pergel ile çizim yapmanın ne demek olduğunu kesin bir hale getirdin. Gelecek sayımızda da bu genel tanımlamayı açıyı üçe bölme problemine uygulayalım.
Gelecek sayıda görüşmek üzere.