Yazar: Cem Tezer
Yıl: 1992-1
Sayı: 6
Bu yazıda, aslında Euclid geometrisinin (izometriler, homotetiler vb. gibi) gerçek anlamda malı olmayan, fakat hem bu geometrideki bazı uygulamaları, hem de Euclid-dışı geometrilere verilecek en basit örneklerin kuruluşu açısından büyük öneme sahip bir dönüşümü, “evirtim’i ele alacağım, Euclid düzlemini $\Delta$ ile gösterelim. Bir $M\in \Delta$ noktası ve bir $\rho \neq 0$ gerçel sayısı gözönüne alalım, “$M$ merkezli ve $\rho$ kuvvetinde bir evirtim” dedigimiz zaman
$\varphi:\Delta -\{M\} \rightarrow \Delta -\{M\}$ (1)
şeklinde (yani düzlemin M dışındaki noktalarını gene düzlemin M dışındaki noktalarına dönüştüren) her $X \in \Delta – \{M\}$ noktasını $MX$ doğrusu üzerinde bulunan ve
$\overline{\rm MX}.\overline{\rm MX’}=\rho$
denklemini sağlayan bir tek $X’ \in \Delta – \{M\}$ (neden?) noktasına gönderen dönüşümü anlıyoruz. (Şekil 1)
$X’ = \varphi(X)$ noktasına “$X$ in evriği” diyeceğiz.
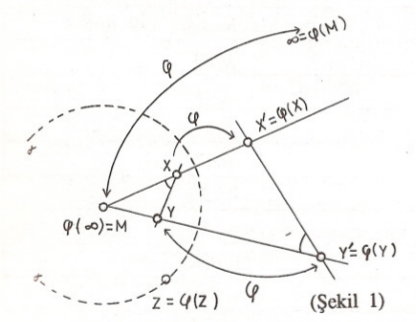
Evirtimin en basit özelliklerine işaret edelim:
a) (1) denkleminde, Hüseyin Demir’in bu dergide incelediği “yönlü uzunluklar” kullanılmakta ([1]). Demek ki $\rho > 0$ ise $X$ ve $X’$ noktaları $MX$ doğrusu üzerinde $M$ nin aynı tarafında, $rho < 0$ ise ters tarafında kalmaktadırlar.
b) (1) denkleminde $X$ ve $X’$ birbirleriyle yer değiştiği zaman, söz konusu denklem değişmeyecektir. Demek ki $\varphi(X) = X’$ iken $X= \varphi(X’)$ dür. Yani bir noktanın evriğinin evriği daima kendisidir.
c) $\rho > 0$ olsun. Merkezi $M$, yarıçapı $\rho^{1/2}$ olan $\gamma$ çemberini ele alalım, $\varphi$ evirtimi altında, $\gamma$ nin içindeki noktalar ($M$ hariç) $\gamma$ ‘nın dışına, dışındakiler de içine gidecektir. Tabii bu arada $\gamma$ üzerindeki her nokta sabit kalacaktır.
Yorum: b) ve c) de bahsedilen hususlar evirtimin yansımaya benzerliklerini ortaya çıkarıyor. Gerçekten de evirtimi, bir doğruya göre değil de bir çembere göre yansıma olarak görmek mümkün (dilimizdeki eski metinlerde evirtimin “akis” olarak adlandırılmasının nedeni herhalde bu).
d) Neden, evirtim için “Euclid geometrisinin gerçek anlamda malı değil” dedim? Bu derin konuya sadece dokunmak istiyorum: Örneğin, bu dönüşüm her zaman doğruları, doğrulara dönüştürmez: Yukardaki gösterimle $\varphi$ evirtimi $\gamma$ çemberinin dışını içine gönderiyor; bu koşullarda $\gamma$ ‘nın dışında bir doğru, doğru olarak kalabilir mi? Mızrak çuvala sığmayacaktır.
e) Yukarıdaki gösterimle, $\rho>0$ halinde $\gamma$ çemberi $\varphi$ evirtimi tamamen belirlemekte. Bu nedenle $\varphi$ ‘ye “$\gamma$ çemberine göre evirtim” diyeceğiz. Ayni şekilde pozitif kuvvetli belirli bir evirtim söz konusu iken, o evirtimi belirten çemberi “evirtim çemberi” olarak anacağız. Evirtim çemberinin evirtim altında sabit kalan noktalardan oluştuğuna tekrar işaret edelim.
Yorum: Okuyucu yarıçapı sanal çemberlere bir anlam biçebiliyorsa bu söz dağarcığını kuvveti negatif evirtimlere de genişletilebilir.
f) Evirtim merkezinin evriğinin bulunmaması bir eksiklik hissi veriyor. Bu eksiklikten kurtulmanın bir yolu da var: Düzlemde hareketli bir noktanın evirtim merkezine gittikçe yanaştığını düşünelim. Bu noktanın evriği evirtim merkezinden istenildiği kadar uzağa gidecektir. Düzlemimizi $\infty$ ile göstereceğimiz “sonsuzdaki nokta”yı eklemekle genişletirsek, evirtim merkezi ve $\infty$ evrik noktalar addolunabilir.
Şimdi evirtimi biraz daha derinlemesine inceleyebiliriz:
Yardımcı Teorem 1:
$M$ merkezli bir evirtimi alalım. $X,Y\neq M$ noktalarının evrikleri sırasıyla $X’,Y’$ noktaları ya doğrudaş ya da çemberdeştir.
İspat: (Şekil 1) Evirtim kuvveti $\rho$ olsun. Bu noktaların doğrudaş olmadıklarını varsayalım.
$\overline{\rm MX}.\overline{\rm MX’}=\rho= \overline{\rm MY}.\overline{\rm MY’} $
den $OXY$ ve $OY’X’$ üçgenlerinin ters benzer oldukları, bu nedenle de
$\sphericalangle (XX’, XY) = \sphericalangle(YX’, Y’Y)$ (2)
olduğu görülür. (Dikkat: “Doğrular arasındaki açı”, bkz. [3]). Demek ki $X,Y,X’,Y’$ noktaları çemberdeştir.
Teorem 1:
a) Bir evirtim, evirtim merkezinden geçen bir doğruyu kendisine dönüştürür.
b) Bir evirtim evirtim merkezinden geçmeyen bir doğruyu, evirtim merkezinden geçen bir çembere dönüştürür. Bu çemberin evirtim merkezinden geçen çağı doğruya diktir.
b’) Bir evirtim evirtim merkezinden geçen bir çemberi, bu çemberin evirtim merkezinden geçen çapına dik bir doğruya dönüştürür. (Sekil 2)
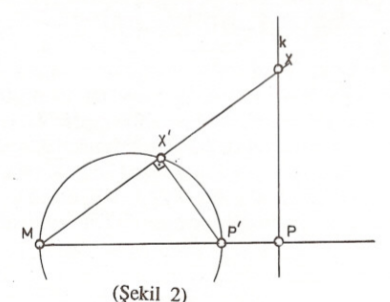
İspat:
a) Evirtim merkezi $M$ olsun. $M$ den geçen bir $s$ dogrusu alalım. (Bu Sekil 2’de yok!) $s$ doğrusu üzerindeki herhangi bir $X \neq M$ noktasının evriği (evirtimin tanımından!) gene $MX = s$ doğrusu üzerinde kalmalıdır. Demek ki $s$ doğrusu kendine dönüşmektedir. (Dikkat: Doğru üzerindeki noktalar yer değiştiriyor ama doğru bütün olarak sabit kalıyor!)
b) $k, M$ den geçmeyen bir doğru olsun. $M$ ‘den $k$ ‘ye indirilen dikmenin ayağı $P$ olsun. $P$ ‘nin evriği $MP$ üzerinde bir $P’$ noktasıdır. Simdi $k$ doğrusu üzerinde herhangi bir $X$ noktası düşünelim. $X$ in evriği $X’$ olsun. Yardımcı Teorem 1’e göre $X,X’,P,P’$ noktaları çemberdeştir. $MP$, $k$ ‘ye dik olduğuna göre $X’P’$ de $MX’$ ye dik olmalıdır. Böylece $X’$ daima $[OP’]$ çaplı çember üzerinde kalacaktır.
b’) Bir noktanın evriğinin evriği kendisi olduğundan bu, b) den aşikardır.
Yorum: Teorem 1 b’) nün önemli bir sonucu olarak evirtim merkezinde birbirine teğet olan iki çember, paralel iki doğruya dönüşecektir.
Yorum: Teorem 1 doğruları çemberlere dönüştürüyor; yani bir anlamda bizi doğruları çember olarak görmeye yöneltiyor. Gerçekten de $M$ noktası hariç çember üzerindeki noktalar doğru üzerindeki noktalarla birebir ilişki içinde bulunuyor. Doğru üzerinde ise $M$ ‘ye karşılık gelen bir nokta yok! Eğer, düzlemimize $\infty$ noktasını ekler, düzlemimizdeki her doğrunun da $\infty$ dan geçtiğini düşünürsek bu durum ortadan kalkar. Yani evirtim konusunda doğruları $\infty$ ‘dan geçen çemberler olarak görmek yararlı olacaktır. Bundan önceki yorumun ışığında da paralel doğrular $\infty$ ‘da birbirine teğet çemberler olarak anlaşılabilir.
Teorem 2: Bir evirtim evirtim merkezinden geçmeyen bir çemberi evirtim merkezinden geçmeyen bir çembere çevirir. Evirtim merkezi aynı zamanda bu iki çemberin bir homoteti merkezidir. (Evirtim kuvveti pozitifse dış, negatifse iç homoteti merkezi, bkz. [1])
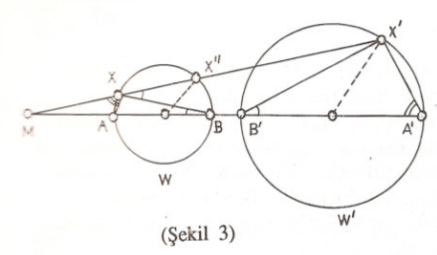
İspat: (Şekil 3) $M$ merkezli bir evirtim ve $M$ den geçmeyen bir $\omega$ çemberi alalım. $\omega$ ‘nın $M$ ‘den geçen çapı $[AB]$ olsun. $A$, $B$ nin evrikleri sırasıyla $A’, B’$ olsun. $\omega$ üzerinde herhangi bir $X \neq A,B$ noktası için $AX, BX$e diktir. $X’, X$ noktasının evriği ise Yardımcı Teorem 1’den $A, X, X’, A’$ noktaları çemberdeş olup
$\sphericalangle (XM, XA) = \sphericalangle(A’X’, A’B’)$ (2)
Aynı şekilde $B, X, X’, B’$ noktalarının çemberdeşliğinden
$\sphericalangle(XB, XX’)= \sphericalangle(B’A’,B’X’)$ (3)
bulunur. (2) ve (3) denklemlerinin sol taraflarının toplamı bir dik açı, sağ taraflarının toplamı da $\sphericalangle (A’X’, B’X’)$ vereceğinden, $A’X’$ daima $B’X’$ ne dik olmalıdır. Yani $\omega$ çemberi üzerindeki her $X$, noktasının evriği (yani $X’$) daima $[A’B’]$ çaplı $\omega’$ çemberi üzerinde kalmalıdır. Simdi, $M$ noktasının $\omega ,\omega’$ çemberlerinin homoteti merkezi olduğunu göstermek kalıyor: $MX$ doğrusu $\omega$yı $X$ haricinde bir de $X”$de kessin. (Özel hal: $MX$, $\omega$ ya teğetse $X= X”$). Evirtimin kuvveti $\rho > 0$ olsun. ($\rho<0$ hali benzer şekilde ele alınabilir.)
$\overline{\rm MX}.\overline{\rm MX’}=\rho$ (4)
Ayrıca $MXB$ ve $MAX’$ üçgenlerinin ters benzerliğinden
$\overline{\rm MX}.\overline{\rm MX”}= \overline{\rm MA}.\overline{\rm MB}=d>0$ (sabit!) (5)
dir (4) ve (5) bölünerek (nasıl?)
$\overline{\rm MX’}:\overline{\rm MX”}=\rho /d=sabit>0$
bulunur. Demek ki $M$, $\omega$ ve $\omega$’ nün dış homoteti merkezidir.
Yorum: Doğruları da genelleştirilmiş çemberler olarak görürsek, Teorem 1 ve 2 “Bir evvirtim çemberleri çemberlere dönüştürür!” şeklinde sloganlaştırılabilir.
Okuyucuyu uyaralım: Genel olarak çember merkezleri, çember merkezlerine dönüşmez.
Yorum: Teğet iki çember bir evirtim altında gene teğet iki çembere dönüşür. Değme noktasının evriği, evrik çemberlerin değme noktasıdır. Okuyucu bunu evirtimin bire-bir bir dönüşüm olması gerçeğinden yola çıkarak, kolayca ispat edebilir.
Örnek I: İçinde çok sayıda çember bulunan problemler evirtim sayesinde basitleştirilebilir:
Problem 1: $\alpha, \beta, \gamma, \delta$ çemberlerini göz önüne alalım. $\alpha$ ve $\beta$, $\beta$ ve $\gamma$, $\gamma$ ve $\delta$, $\delta$ ve $\alpha$ sırasıyla $A,B, C, D$ noktalarında teğet olsun. (Şekil 4a) $A, B, C, D$ noktalarının çemberdeş olduklarını gösteriniz.
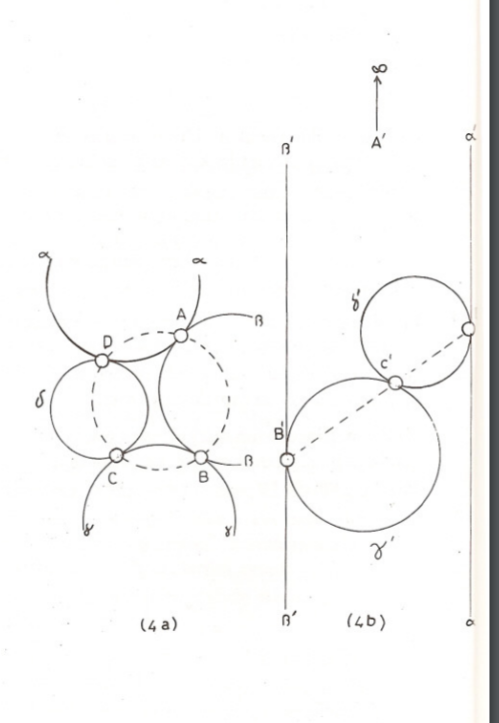
Çözüm: A noktası merkez olmak üzere bir evirtim alalım, $\alpha$ ve $\beta$ çemberleri $\alpha$’, $\beta$’ paralel doğrularına dönüşecektir. $\gamma$, $\delta$ çemberlerinin evrikleri $\gamma$’, $\delta$’ ise $\alpha$’ doğrusu $\delta$ çemberine $D$’nin evriği olan $D$’ de, $\beta$’ doğrusu $\gamma$’ çemberine $B$ nin evriği olan $B$’ de değerken, $\beta$’ ve $\gamma$’ çemberleri de $C$ nin evriği $C’$ noktasında birbirlerine teğet olurlar. (şekil 4b) Şimdi işimiz $B’, C’, D’$ noktalarının bir doğru (yani $A$ nın evrigi olan $\infty$ dan geçen bir çember) üzerinde kaldığını göstermeye kalıyor. Bunu okuyucu kolayca yapabilir. (İpucu: $C’$ deki teğet $B’C’$ ve $C’D’$ kirişleriyle aynı açıları yapar.)
Örnek II
İlk örneğimizde evirtimin kuvveti önemli değildi. Bazen evirtim kuvveti akıllıca seçilirse, problemler basitçe çözülebilir.
Problem 2: Bir $ABC$ üçgeninde üç yüksekliğin kesişme noktası $H$, sırasıyla $BC$, $CA$, $AB$ kenarları üzerindeki yükseklik ayakları da $U, V, W$ olsun. $[HA]$ çaplı çember $ABC$ üçgeninin çevrel çemberini bir $K\neq A$ noktasında, $UVW$ üçgeninin çevrel çemberi de $BC$ doğrusunu bir $L\neq U$ noktasında kessin. $K, H, L$ noktalarının doğrudaş olduklarını gösteriniz.
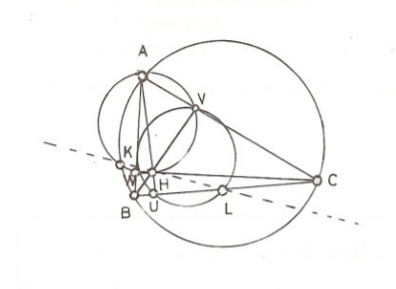
Çözüm: Önce
$\overline{\rm HA}.\overline{\rm HU}= \overline{\rm HB}.\overline{\rm HV}= \overline{\rm HC}.\overline{\rm HW} $ (6)
olduğunu hatırlayalım. (Örneğin $HAV$ ve $HBU$ üçgenlerinin benzerliğinden ilk eşitlik, $HCV$ ve $HBW$ üçgenlerinin benzerliğinden de ikinci eşitlik bulunabilir.) Sonra da $H$ merkezli ve $\rho = \overline{\rm HA}.\overline{\rm HU} $ kuvvetinde bir evirtim alalım. (6) eşitliğine göre $U, V, W$ sırasıyla $A, B, C$nin evrikleridir. Öte yandan $ABC$nin çevrel çemberi $UVW$ nin çevrel çemberine dönüşecektir. En nihayet $[HA]$ çaplı çember aynı zamanda $V$ ve $W$ den de geçtiği için (Neden?) $BC$ doğrusuna dönüşmelidir. Demek ki $ABC$ nin çevrel çemberiyle $[HA]$ çaplı çemberin $A$ olmayan kesişim noktası $K$, söz konusu evirtim altında $UVW$ nin çevrel çemberiyle $BC$ doğrusunun $U$ olmayan kesişim noktasına yani $L$ye gitmelidir. Bir nokta, evirtim merkezi ve evrik nokta daima doğrudaş olduğundan, $K, H, L$ noktaları da doğrudaştır.
Yorum: Bilgili okuyucu $UVW$ nin çevrel çemberini ABC üçgeninin dokuz nokta çemberi olarak tanıyacaktır. Ayrıca $L$ noktası da $[BC]$ nin orta noktasıdır. Dokuz nokta çemberini ve ilgili dokuyu az ilerde kısaca tanıtacağız.
Yorum: Geniş açılı üçgenlerde $\rho =\overline{\rm HA}.\overline{\rm HU}>0$ olduğundan, yukarıda söz konusu olan evirtimde, $H$ merkezli ve $\rho^{1/2}$ yarıçaplı çembere evirtim çemberi olarak bakılabilir. Bu önemli çembere üçgenin kutup çemberi adı verilir. Tabii, dar açılı üçgenlerde kutup çemberi sanaldır.
Örnek III
Evirtim uzaklıkları saklı tutmamakla birlikte, bu yönde de önemli ipuçları sağlayabilir. Okuyucu bu örnekte, evirtim merkezinin ayrı zamanda evrik çemberlerin homoteti merkezi olduğu hususunun nasıl etkili bir araç olduğunu görecektir. Örneğimiz, Pappus’a (M.S. 4. Yüzyıl) izafe edilen bir teorem olacak. Önce biraz karışık olan dokuyu açıklayalım: (Sekil 6)
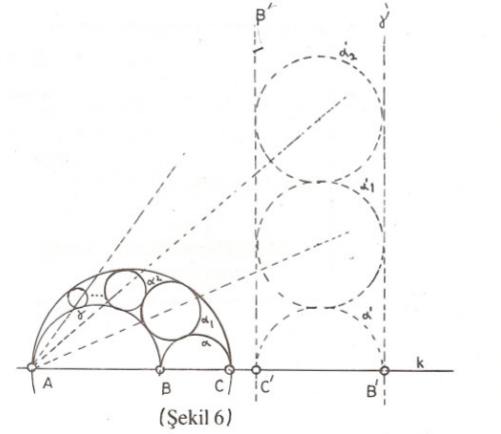
Bir $k$ doğrusu üzerinde birbirlerinden farklı $A, B, C$ noktaları alalım. B noktası, A ile C arasında bulunsun. $\alpha$, $\beta$, $\gamma$ sırasıyla $[BC]$, $[CA]$, $[AB]$ yarıçaplı $k$ nın ayrı tarafında kalan yarıçemberler olsun. Böyle üç çemberin oluşturduğu şekil eski Yunan matematikçileri tarafından incelenmiş ve ayakkabıcı bıçağı anlamında “arbilos” olarak adlandırılmıştır. (Arbilos hakkında birkaç güzel teorem Arsimed’in (M.Ö. 3. yüzyıl, Ölüm 212) aslı değil Arapça aktarmaları bulunan bir eserinde görülmekte [2]). Şimdi “arbilos”un içine $\alpha$, $\beta$, $\gamma$ yarı çemberlerinin her birine teğet bir $\alpha_1$ çemberi yerleştirelim. Bundan sonra gene “arbilos”un içine $\alpha_1$ çemberine ve $\beta$, $\gamma$ yarı çemberlerine teğet bir $\alpha_2$ çemberi yerleştirelim. Devamla “arbilos”un içine $\alpha_2$ çemberine ve $\beta$, $\gamma$ yarı çemberlerine teğet olup $\alpha_1$ olmayan bir $\alpha_3$ çemberini yerleştirelim. Tanımımızı tümevarımla tamamlayalım. $\alpha_1, \alpha_2 ,\dots, \alpha_n$ çemberlerinin tanımladığını varsayarak $\alpha_{n+1}$i “arbilos”un içinde kalıp, $\alpha_n$ çemberine ve $\beta$, $\gamma$ yarıçemberlerine teğet olup $\alpha_{n-1}$ olmayan tek çember olarak tanımlayalım.
Teorem 3: $\alpha_n$ çemberinin $k$ doğrusuna uzaklığı, bu çemberin çapının $n$ katıdır.
İspat: Püf noktasını teşkil eden evirtimi verip, ispatı okuyucuya bırakacağız: $A$ merkezli bir evirtim alalım. (Sekil 6’da pozitif kuvvetli bir evirtim tasvir ediliyor.) $B$ ve $C$nin evrikleri $C’$ ve $B’$ olsun. $\beta$ ve $\gamma$ yarı çemberleri $k$ doğrusuna sırasıyla $C’$ ve $B’$ de dik yarı doğrulara dönüşürken $\alpha$ yarı çemberi $[B’C’]$ çaplı $\alpha’$ yarıçemberine dönüşecektir. $\alpha_1$ ,$\alpha_2$ ,$\dots$ ,$\alpha_n$, çemberlerinin evrikleri de $\beta’$ ve $\gamma’$ doğrularına teğet olup $\alpha’$ yarıçemberinin üzerine bir kule şeklinde istif edilmiş çemberler olacaktır. Son ipucu: $A$ noktası $\alpha_n$, ve $\alpha’$ nün homoteti merkezidir.”
KAYNAKLAR
1) H. Demir, “Homoreti ve Benzerlik”, Matematik Dünyasi, Sayı 4, s.2-7.
2) EJ. Dijksterhuis, “Archimedes”, Ejnar Munksgard, Kopenhag, 1956. (c.Dikshorn tarafından Felemenkçe aslından İngilizce’ye tercüme)
3) C.Tezer, “Düzlem Geometride Açılar ve Ölçüleri”, Matematik Dünyası, Sayı 1, s. 3-6.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Melih Mert Oskay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

