Yazar: Huriye Önder
Yıl: 1992-2
Sayı: 7
Türkiye’de ve yurt dışında pek çok üniversitede yüksek matematik, analiz, calculus gibi adlar altında, birinci sınıf seviyesinde, matematiğe giriş niteliği taşıyan dersler verilmektedir. Bu dersler türev ve İntegral gibi temel kavramları, bunlarla ilgili yöntem ve uygulamaları kapsamakta olup lise son sınıf matematik dersinin genişletilmiş şekli ve devamı olarak da görülebilir. Calculus Türkiye’de Ve başta Amerika Birleşik Devletleri olmak üzere birçok ülkede fen ve mühendislik dallarından başka biyoloji, hayat bilimleri, işletme, ekonomi, sosyal bilimler vb. çeşitli dallarda öğrenim görmek isteyen öğrencilerin zorunlu olarak aldıkları bir ders. Dersin amacı temel matematik kavramlarını ve metotlarını Öğretmenin yanısıra matematik dışında çeşitli dallarda öğrenim görecek olan öğrencilere kendi konularında uygulayabilecekleri matematiksel yöntemleri ve teknikleri vermek; matematiksel modelleri kurup matematiği uzmanlık alanları İçinde kullanabilmelerini sağlamak. Matematiğin çok ve çeşitli uygulama alanları olduğunu gözönünde bulundurarak calculus’u temel ve çok kullanışlı bir araç olarak kabul edebiliriz. ABD ve Türkiye’deki üniversitelere kısaca bakınca dersin her iki ülkede de ana hatları ve kapsadıği kavramlar açısından aynı olduğunu görüyoruz. Örneğin Amerika genelinde de, ülkemizde Orta Doğu Teknik Üniversitesi’nde de bu dersteki başarısızlık oranı % 30 ile % 50 arasında. Bu iki ülkedeki öğrencilerin sosyal ve ekonomik yapısi çok farklı olmakla birlikte matematik derğlerine bakış açıları ve karşılaştıkları sorunlar arasında büyük benzerlikler var. Calculus dersi, üzücüdür ki, ögrencilerin öğenimlerine devam edebilmeleri için aşmak zorunda oldukları bir engel olarak karşımıza çıkıyor. Öte yandan matematik derslerine başarılı olmuş pek çok öğrenci, matematiğin güzelliğinin ve hayatın hemen her alanında karşımıza çıkabilecek dinamik problemlerin çözümünde sağlayacağı kolaylığın farkında değil. Matematik, öğrencilerin aklında hatırlamaya ve ezberlemeye yönelik karışık yöntemler ve zor formüller dizisi olarak kalıyor; düşünmeye, doğru akıl yürütmeye, algılamaya ve sezgiye dayalı olduğu çoğu zaman anlaşılamiyor. Bu arada geleneksel calculus derslerinde işlenen formüllere ve metotlara dayalı problemleri öğrencilerin eve gidip çözerek, matematiksel düşünen İnsanlar haline dönüşmesini beklemek de oldukça yanlış bir tutum. Dersin kalabalık sınıflarda ve sıkıcı bir biçimde verilmesinin başarısızlığa katkısı büyük. Ayrıca birçok matematik problemini hesap makinesi kullanarak kolayca çözmek mümkün. Örneğin belirli bir integralin çözümü için INT düğmesine basmak artık yeterli. O halde neden matematik derslerinde bu tür mekanik problemlerin çözümü için gerekli tekniklerle zaman kaybedilsin ve öğrenciye düşünme alışkanlığı kazandırabilecek problemler tercih edilmesin?
Öğrencilerin matematik derslerinden gerektiği biçimde yararlanmaları ve calculus’un zevk alınan, ilginç bir ders haline getirilmesi için klasik yaklaşımdan üzaklaşarak yenilikler yapmak gerekli. Yıllar Önce başta Harvard Üniversitesi olmak üzere bilimsel alanda kendisini kanıtlamış birkaç üniversite calculus derslerinde geleneksel tutumdan uzaklaşmışlar ve daha çok kavramaya, düşünmeye ve sezgiye yönelik bir program izlemişlerdir. Bu arada akademik çevrelerin yanısıra akademik olmayan çevrelerce de ABD’nin uluslararası arenada etkin olabilmesi için calculus derslerinde ülke genelinde köklü değişikliklerin yapılması gerektiğine inanılıyor, Özellikle hükümete bağlı kesim ile iş çevrelerinin inancı büyük ölçüde matematik bilen ve kullanabilen teknik elemanlara ihtiyaç olduğu doğrultusunda; bu yüzden derslerin bir filtre değil pompa görevi üstlenmesi gerektiği savunuluyor.
ABD’nde NSF. (Nâtİonal Science Foundâiioii-TÜBİTAK benzeri bir kurum) tarafından desteklenen ve calculus programlarının değişmesini öngören birden fazla proje söz konusu.Projelerin hepside bir ölçüde bilgisayar ve hesap makinelerinden yararlanmayı öngörüyor. Türkiye gibi hesap makineleri ve özellikle bilgİsayarların her kesimde yaygın olarak kullanılmadığı bir ülkede yaşamanın verdiği alışkanlıkla ilk başta programların ülke gerçeklerinden uzak olduğu düşünülebilir; fakat teknolojik gelişmelerden yararlanmak ve onları amaçlarımız doğrultusunda kullanmak çağımızın gereklerinden. Bilgisayar ve hesap makineleri yardımıyla birçok matematiksel kavramı daha iyi anlamak ve görselleştirmek mümkün. Teknolojik gelişmeler dersleri daha verimli ve ilginç kılmak için kullanılabilir; yine de bilgisayarlar matematik derslerinin esas hedefini saptırmamalı ve onlara egemen olup kısırlaştırılmamalı.
Harvard Ünıvetsitesi’nin Stanford University, University Of Arizona, the University of Southern Mississippi, Colgate University; Suffolk Community College ve Chelmsford High School’un katkıları ile yönetmekte olduğu bir projeden bahsetmdk İstiyorum. Bu proje incelenirken gözardı edilmemesi gereken, programın matematik öğrencileri ve araştırmacılardan çok uygulamalı dallarda öğrenim görecek olan öğrencilere yönelik olması. Öngörülen program çerçevesinde Öğrencilerin bilgisayar imkanlarını kullanmaları teşvik edilmiş, pakat programlardan yararlanarak basit sayısal integrasyon, diferansiyel denklemler ve kök bulma işlemleri yapmaları sağlanmıştır. Projede vurgulanan fikir, çağımızın teknolojik olanaklarının kullanımında bilgisayarların ve hesap makinelerinin, mikroskop işlevi görmesidir. Bilgisayar konunun odağı olmak yerine kavramları anlatmaya ve geliştirmeye yarayan bir araç olarak kullanılmaktadır.
Projenin ana hatlarına bir göz atalım. En çok üzerinde durulan “üçler kuralı”. Bu kural mümkün olan her matematiksel kavramın geometrik, sayısal ve cebirsel yaklaşımlarla açıklanması ve aralarında iyi bir denge kurulması şeklinde özetlenebilir. Örneğin türevde zincir kuralı anlatılırken bunun sadece cebirsel bir kural gibi $ sin2x $ türevi olan $2cos2x$ fonksiyonunun grafiğini incelemek ve. dalga boyunun iki katı olmasını sağlayan $ 2$ katsayısın nereden ve niçin geldiğini tartışmak bu kuralın daha iyi anlaşılmasını sağlayabilir. İntegral teknikleri ile öğrenciyi bunaltmak yerine, onlara niçin integral almaları gerektiğini vurgulayacak problemler sorulabilir. Kim $y= \sqrt{x^3}$ eğrisinin yay uzunluğu ile ilgilenir. Bunun yerine bir elipsin çevresini hesaplamak daha ilginç olabilir. Arsanın değerli olması nedeniyle bina yaparken arsanın kullanılmayan kısımlarının alanını en aza indermek, bir üçgenin içine sığabilen en büyük dairenin alanını bulmaktan daha ilginç olabilir. bu örnekleri çoğaltmak mümkün ama esas amaç öğrencinin ilgisini çekerek düşünmesini sağlamak ve grafik yardımıyla kavramları somut olarak görüp anlamasını kolaylaştırmak. Bu arada cebirsel çözümlerden tümüyle uzaklaşılmış değil. Programda birçok matematiksel problem irdelenerek sonucun nicel ve nitel davranışının anlaşılmasına önem veriliyor. Sayısal teknikler de programda yer alıyor.
Geleneksel kitap ve programlarda tam sayılar tercih edilirken; hesap makinelerinin el altında bulunduğu varsayımı ile uygulamalarda kesirli ve yaklaşik rakamların kullanılmasından çekinilmemiştir. Alışageldiğimiz matematik derslerinde trigonometriye geniş bir yer ayrılmakta, trigonometrik ifadeleri içeren integral, türev ve tekniklerin üzerinde uzun uzun durulmaktadır. Üssel fonksiyonlar ve logaritmik fonksiyonlar ise dersin sonlarına doğru görülmekte; hatta türev ve integral konularının işlenmesinden sonra bu tür fonksiyonlarla ilgili uygulama ve tekniklere yer verilmektedir. Önerilen yöntemde ise birçok alana uygulanabilen logaritmik ve üssel fonksiyonlar programın hemen en başında yer alırken; sekant kosekant gibi trigonometrik fonksiyonlarla, türev ve integralleri karışık, cebirsel ve mekanik teknikler gerektiren fonksiyonlara pek yer verilmemektedir. Zorlama problemler yerine daha çok gerçek yaşamdan alınan problemler uygulama için seçilmiştir; fakat fonksiyonlar bazen gerçekte olduğundan daha basite indirgenmiştir. Diferansiyel denklemler ve bunlarla ilgili uygulamalara geleneksel derslerde hemen hiç yer verilmezken, dinamik durumların diferansiyel denklemlere uygulaması, fizik, sosyal bilimler ve hayat bilimlerinden alınan nüfus artışı, üssel artış, lojistik ve yavaşlatılmış artış fonksiyonları, çok değişkenli Lotka-Volterra “av avcı” modeli ve mühendislikte kullanılan “cubic splines” metodu detaylı bir şekilde işlenmiştir.
Programın çarpıcı taraflarından birisi de lokal ve global bakış açısının dikkatlice ayrılmış olması. Örneğin, sabit bir noktadaki türevle fonksiyonun türevinin ne anlama geldiği dikkatlice yazılmış ve bu iki kavram birbirinden ayrılmıştır. Lokal bakış açısı, yaklaştırma tekniklerine ve hata analizine imkan tanımaktadır. İntegral için de aynı yaklaşım söz konusudur. İntegral, belirli integral ve türevin ters işlemi olarak ayrı ayrı incelenmiş ve belirli integralde yaklaştırma teknikleri, sayısal integrasyon ve yine hata analizine yer verilmiştir.
Geniş kapsamlı değişiklikler içeren böyle bir projenin oluşturulması ve uygulanması çeşitli zorlukları da beraberinde getiriyor. Uygulamada ilk akla gelen güçlük yaygın bilgisayar kullanımını gerektirmesi olabilir. Ama zorluklar bununla bitmiyor. Geleneksel yaklaşımdaki programları değiştirmek temel olmakla birlikte aşamalardan sadece birisi. Bu tür bir projeyi ortaya çıkarabilmek veya uygulayabilmek için yadsınamayacak oranda bilgi birikimi ve araştırmaya yönelik matematik bilgisi gerekmektedir. ABD’nde söz konusu projeye katılan kuruluşlar bir yandan programı geliştirirken bir yandan daprogramı uygulamak isteyen yüksek okul ve liselerdeki öğretim elemanlarını bilgilendirmek ve eğitmek için çaba sarfetmektedirler. Temel matematik derslerinin içeriğinde köklü değişiklikler getiren bir programın uygulamaya geçirilmesinde geleneksel materyal ve kitaplar yetersiz kalmaktadır. Sağlıklı bir uygulama için yeni fikir ve tekniklerin kullanıldığı alıştırma problemlerine yer veren uygun kitap ve notların yaçılması da zorunlu olarak proje kapsamına girmektedir.
Türkiye’de de matematik derslerine ülke yapısına uygun, yenilikçi ve özgün eğitim projeleri ile benzer yenilikler ve değişiklikler getirilmesi olumlu bir gelişme olacaktır.
Aydınlatıcı olması bakımından aşağıda bu programda kullanılan birkaç problemi sıralıyorum.
1.${\frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1 } $ denklemi ile verilen elipsin çevresini hesaplayınız.
Yanıt: Yayın uzunluğu formülünden, çevre${ \int_0 ^{2\pi}} {\sqrt{a^2sin^2 + b^2cos^2}tdt} $ integraline eşittir. Bu integral ${a\neq b}$ hali için bilinen tekniklerle hesaplanamaz. Alışageldiğimiz derslerde ve kitaplarda öğrencilere bunun eliptik bir integral olduğu ve bilinen fonksiyonlar cinsinden hesaplanamayacağı söylenerek konu kapatılır. Bu doğru olmakla birlikte sayısal integrasyon teknikleri ile bu integral dolayısıyla da elipsin çevresi yaklaşık olarak hesaplanabilir. Bu da $2\sqrt{ab} \pi $ ve $(a+b)π$ gibi yaklaşık formüllerin anlaşılmasında ve öneminin kavranmasında iyi bir yoldur.

2. Tabloyu kullanarak
a)$ y=f(x)’e$ $ x=0.6 $noktasında teğet olan doğrunun (yaklaşık) denklemini yazın.
Yaklaşık yanıt : $ y=0.26x+3.74 $
b)$f(0.7),f(1.2)$ ve $f(1.4)$ değerlerini yaklaşık olarak hesaplayın. Bulduğunuz sonuçlardan hangisi daha güvenilirdir? Neden?
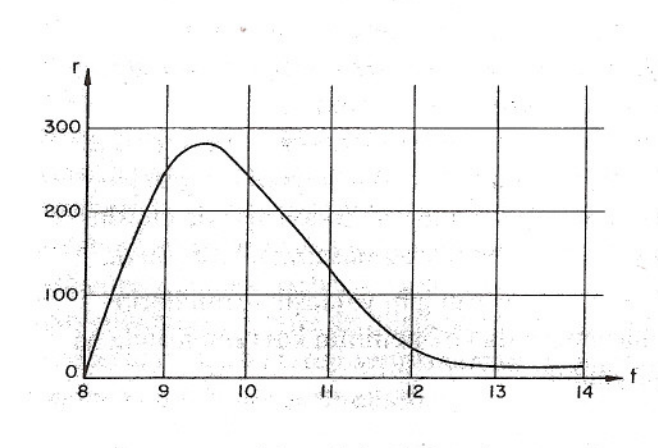
3. Bilet satan bir kulübe saat 9.00’da açılmakta ve saatte ortalama $200$ kişiye hizmet vermektedir. Aşağıdaki grafik bilet kuyruğundaki insan sayısının zamana $ (t) $ göre değişme hızını $(r)$ göstermektedir,
a) Saat 10.00’da bilet kuyruğunda kaç kişi kaldığını hesaplayın.
Yaklaşık yanıt : $200$ kişi.
b) Kuyruktaki insan sayısının en fazla olduğu saati bulun.
Yaklaşık yanıt : $10.20$
c) Kuyrukta ne zaman hiç kimse kalmaz?
Yaklaşık yanıt : $12.20$
Soruları cevaplarken hız ve alan ile türev ve integral arasında bir ilişki kurmaya çalışın.
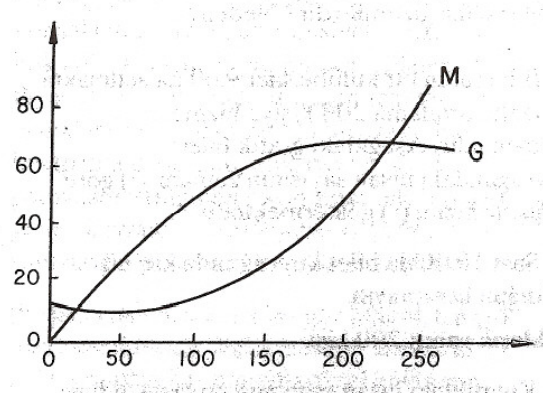
4. Aşağıdaki grafikte toplam maliyet $M$ ve toplam gelir $G$ ile bir birim $1000 $ $ olmak üzere gösterilmiştir. Grafiği kullanarak maksimum kârı hesaplayın. Cevabınızı türev kullanarak açıklayın.
Yaklaşık yanıt : $40.000 $ $
5. $100 $ milyon litre su kapasiteli bir depo, bir yerleşme merkezine $1$ milyon litre su sağlamaktadır, Deponun bir kısmı günde $0.9$ milyon litre su sağlayan bir pınardan, geri kalan $ 0.1$ milyon litresi de yakındaki bir dereden sağlanan sularla yeniden doldurulmaktadır. Pınarın suyu hiç tuz içermezken, dere suyunda $1$ litrede $ 0.001$ gr. oranında tuz bulunmaktadir. Başlangıçta deponun su ile dolu olduğunu ve içinde hiç tuz olmadığını biliyoruz. Herhangi bir anda depodaki su ve tuzun homojen olarak karışmış olduğunu varsayalım. Depo içerisindeki tuz oranını zamana bağlı bir fonksiyon alarak çiziniz.
Yanıt : $ r=10^{-5}$ ($1 – e^{-0.004}$)

6. Hesap makinesikullanarak $x$’in yeteri kadar büyük değerleri için $( 1+ \frac{1}{x})^x$ ifadesinin $1$’e eşit olduğunu gösterin. Sizce bu neden oldu?
Kaynakça 2, 3, 4. Gotdöh, Sheldbn P., İ-İughes Hallet; Deborâh. (1991). “Calculuş Refötm Ahd İts linplications for TWO*Yeat Colleges.”The AMATCY Revidw, 12(2), 50-57. research•CogncİJ (1989). EvgybQdy Washington, DC: National Academy Press. Hughes Halleçl)eborah, ve, Andrew ve diğerleri (1990). Cote Calculüs Consortium (yayınlanacak). Taylor, Peter Da, An Intröductionto theAnalysis öf Functions (yayınlanacak).
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

