Yazar: Uluğ Çapar
Yıl: 1992-5
Sayı: 10
Konveks, $n$ kenarlı bir çokgenin bütün köşegenlerinin çizildiğini düşünelim. Bu yazıda şu iki problemin yanıtı aranacaktır:
$A) \quad$ Çokgen içinde en fazla kaç kapalı alt bölge onaya çıkar?
$B) \quad$ Çokgenin köşegenleri en fazla kaç doğru parçasına bölünürler?
Çokgen içinde herhangi bir noktadan en fazla iki köşegen geçtiği varsayımı yapılırsa bu sorular şöyle de sorulabilir: Bütün köşegenlerinin çizilmesi ile
$A’) \quad$ Çokgen içinde kaç kapalı alt bölge meydana gelir?
$B’) \quad$ Köşegenler toplam olarak kaç doğru parçasına bölünürler?
Yukardaki soruların cevabı olan formüller önce çetrefil bir sayma işlemi sonucu $n$’e göre indirgeme bağıntılarının bulunması, daha sonra da bu indirgeme bağıntıları üzerinde bir hayli cebrik işlem yapılması ile elde edilebilir. Bu bize $n$’e göre 4’üncü dereceden polinomlar verir. Oysa aynı formüller kombinatorik olarak aşağıda açıklanan biçimde çok kolay olarak çıkarılabilmektedir.
A’) nın yanıtı:
Köşegenleri herhangi bir biçimde numaralayalım. (Toplam köşegen sayısı $\binom{n}{2} -n$dir, (Niçin ?)). Bu köşegenlerin teker teker çizildiğini varsayalım ve bu sırada ortaya çıkan alt bölgeleri izleyelim. Başlangıçta tek bir bölgemiz vardır. (Çokgen kenarları ile sınırlanan kapalı bölge). 1 no.lu köşegenin çizilip karşı köşeye ulaşması ile iki alt bölge yaratılmış olur, dolayısı ile bölge sayısı bir artar. Daha sonra köşegen çizim işlemine devam ederek $j$’inci köşegene kadar geldiğimizi düşünelim. (Şekle bakınız). $j$inci köşegenin çizimi sırasında daha önce çizilmiş bulunan köşegenlerle her kesişmemizde alt bölge sayısını bir artırmış oluruz. Örneğin $j$inci köşegenin daha önce çizilmiş bulunan $BC$ köşegeni ile $Q_1$ noktasında kesişmesinden sonra $ADC$ bölgesi, $ADQ_1$ ve $AQ_1C$ olarak iki alt bölgeye bölünür, diğer bütün alt bölgeler ise aynı kalır. Dolayısı ile toplam alt bölge sayısı bir artar. j inci köşegenin daha önce çizilmiş olan köşegenlerle $Q_2 , Q_3 , \dots $ gibi diğer kesişme noktalarında da alt bölge sayısı birer artmağa devam eder. Sonuncu kesişme noktası, (diyelim ki $Q_s$)’ten başlayıp karşı köşeye ulaşım sırasında da alt bölge sayısı bir artar. ($SRT$ bölgesi, $SRQ_s$ ve $Q_sRT$ olarak iki alt bölgeye bölünür).
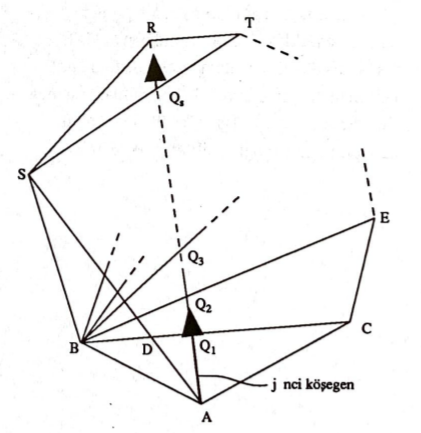
Bütün köşegenler çizildikten sonra şu sonuca varılır:
i) Bu çizim sırasında bütün köşegen kesişme noktalan elde edilir, ayrıca varsayımımızın sonucu olarak da her bir köşegen kesişme noktası bir ve yalnız bir kere göz önüne alınır. (Köşegen kesişme noktalan sayısı $\binom{n}{4}$tür. (Niçin ?)).
ii) Her bir köşegen kesişme noktası ortaya çıktıkça alt bölge sayısı bir artar. Her bir köşegenin karşı köşeye ulaşması ile de alt bölge sayısı yine bir artırılmış olur.
Karşı köşeye ulaşma işlemi köşegen sayısı kadar yinelenir.
Böylece başlangıçta tek bir bölge ile yola koyulduğumuzdan:
Alt Bölge Sayısı = 1 + Köşegen Kesişme Noktası Sayısı + Köşegen Sayısı
bağıntısı elde edilir. Diğer bir deyişle $A’)$ sorusunun yanıtı
$$1 + \binom{n}{4} + \binom{n}{2} -n$$
dır.
$B’)$ Benzer bir akıl yürütme ile:
Köşegenler Üzerindeki Doğnı Parçası Sayısı = 2 x Köşegen Kesişme Noktası Sayısı + Köşegen Sayısı,
bağıntısı veya $B’)$ sorusunun yanıtı olarak
$$2\binom{n}{4} + \binom{n}{2} -n$$
formülü bulunur.
Bu defa çizime sıfır doğru parçası ile başlanmakta, $Q_1, Q_2, \dots, Q_3$ gibi kesişme noktalarında ise doğru parçası sayısı iki artmaktadır. (Örneğin $Q_1$ kesişiminde DC doğru parçası yerine $AQ_1, DQ_1$ ve $Q_1C$ gibi üç doğru parçası ortaya çıkmaktadır). Bunun gibi karşı köşeye ulaşım da yeni bir doğru parçası yaratmaktadır, ($Q_3R$ gibi). Okuyucu ikiden fazla köşegeni aynı noktadan geçmeyen konveks çokgenler çizerek aşağıdaki sayısal değerleri kontrol edebilir:
| n | 4 | 5 | 6 | 7 | 8 | 9 |
| Alt Bölge | 4 | 11 | 25 | 50 | 91 | 154 |
| Doğru Parçası | 4 | 15 | 39 | 84 | 160 | 279 |
Bu değerlerin bazıları kristallografi ve mineralojide kullanılmaktadır.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Umut Gür‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

