Yıl: 1993-1
Yazar: Ali Doğanaksoy
18 inci Yüz yılın ortalarında Königsberg şehri Pregel nehrinin iki yakası ve nehirdeki iki ada üzerine kurulmuştu. Bu adalardan büyük olanı şehrin iki yakasına ikişer köprü; diğeri de birer köprü ile bağlanmıştı. Aynca iki ada arasında da bir köprü bulunmaktaydı.
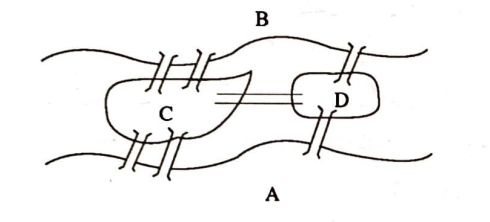
Şehir sakinlerinin cevaplandırmaya çalıştığı bir soru vardı: Her hangi bir noktadan harekete başlayıp, yedi köprünün hepsinden bir ve yalnız bir kez geçip, şehrin bütün bölümlerini dolaştıktan sonra başlangıç noktasına varılabilir mi? Bu problemin çözümü olmadığı Leonhard Euler (1707-1783) tarafından gösterildi. Euler, problemi üzerinde daha rahatça oynayabilecek bir şekille temsil ederek işe başladı. Şehrin dört bölümü birer nokta ve köprüler de bu noktaları bağlayan eğri parçaları ile gösterilirse probleme ait şekil şöyle olur:
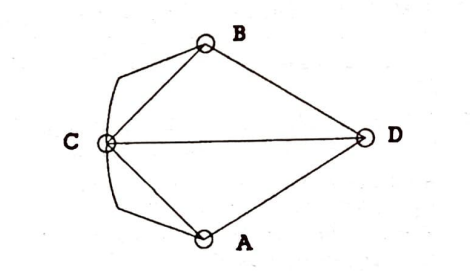
Elbette bu şekli, problemin özelliklerini bozmadan şeklinde de çizebilirdik:
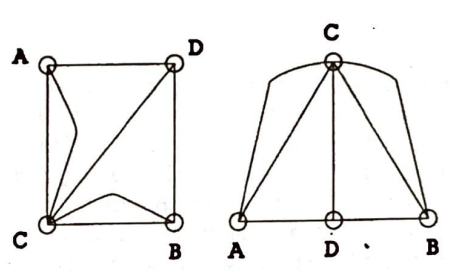
Şehirleri temsil eden noktalara düğüm köprülere tekabül eden eğri parçalarına da kiriş adını verelim. Königsberg köprüleri problemi bu çizdiğimiz şekiller dilinde şu hali aldı: Herhangi bir düğüm noktasından harekete başlayıp, bütün kirişlerden bir ve yalınız bir defa geçerek, bütün düğümleri ziyaret ettikten sonra başlangıç düğümüne varabilir miyiz? Böyle bir gezintinin imkansızlığını göstermeden önce bir iki tanım daha yapalım. Her kirişin iki ucunda birer düğüm bulunmaktadır. Bu düğümlere o kirişin uçları denebilir. Aralarında (en az) bir kiriş bulunan iki düğüme komşu düğümler ve ortak bir ucu bulunan iki kirşe de komşu kirişler diyelim. Bir düğümü uç kabul eden kirişlerin sayısı, uğraştığımız problemde ve bir çok tartışmada önemli rol oynamaktadır. Bu sebeple bu sayıya da bir isim vermek yerinde olur. Buna (yerel) derece diyeceğiz. Bu tanımlardan sonra probleme dönmeden önce bir gözlemde bulunalım. Sadece Königsberg köprüleri problemi için çizdiğimiz şekilde değil, düğümler ve kirişlerden oluşan benzer herhangi bir şekilde bir düğümden başlayıp bütün kirişleri bir ve yalnız bir defa kullanarak ve bütün düğümleri ziyaret edip başlangıç noktasına varmak istediğimizi düşünelim. Derecesi tek olan bir düğüm başlangıç düğümü olamaz zira, buna bağlı kirişlerden birisi harekete başlarken çıkış kirişi olarak kullanılacaktır, geriye bu düğüme bağlı çift sayıda kullanılmamış kiriş kalacaktır. Bu düğümü ikinci kez ziyaret etliğimizde, buna varmak için bir kiriş daha kullanılmış olacağından geriye tek sayıda (yani en az 1) kiriş kalacaktır, demek ki bu düğüm hareketin bieceği nokta olamaz.

Öte yandan derecesi tek olan bir düğüm ara düğüm de olamaz (neden?). O halde, problemin bir çözümü olabilmesi için bütün düğümlerde derecenin çift olması gerekir. Oysa, Königsberg köpüleri için çizdiğimiz şeklin bütün düğümleri tek dereceli. Yani problemin çözümü yoktur.
Şimdi bir nehrin kenarında lahanası, kuzusu ve kurdu ile düşünen adamın problemine bir bakalım. Adam karşı kıyıya geçmek istiyor ama kuzu ile lahanayı, kurt ile de kuzuyu başbaşa bırakmıyor. Karşıya geçerken kullanabileceği kayık ise o kadar küçük ki, adam her seferinde yanına ancak bir tek şey alabiliyor. Karşımıza çıkabilecek bütün halleri şu şekilde gösterebiliriz:

Bu şemalarda başlangıç konumumuz 1; varmak istediğimiz konum 16. Adam, lahana ve kuzuyu baş harfleri ile; kurdu da R harfi ile temsil ediyoruz. Kuzunun lahanayı veya kurdun kuzuyu yiyebileceği istenmeyen konumlar ise 5, 6, 8, 9, 11 ve 12. Bir konumdan hangi konumlara geçebileceğimizi gösteren bir tablo hazırlayalım.

Bu tabloyu düğümler ve kirişler kullanarak şöyle gösterebiliriz:
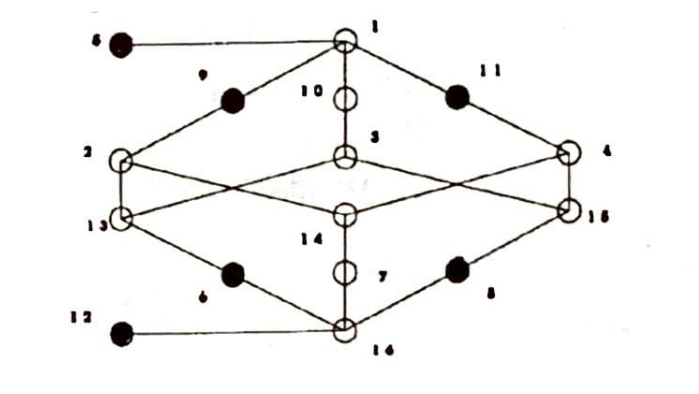
$T$ adını verdiğimiz bu şekilde, düğümler problemin konumlarını kirişler de konumlann hangileri arasında geçiş olduğunu göstermektedir. Siyah düğümler istenmeyen konumlara tekabül etmektedir. Bunları ve bunlara bağlı kirişleri silersek yeni bir $T_1$ şekli elde edilir:
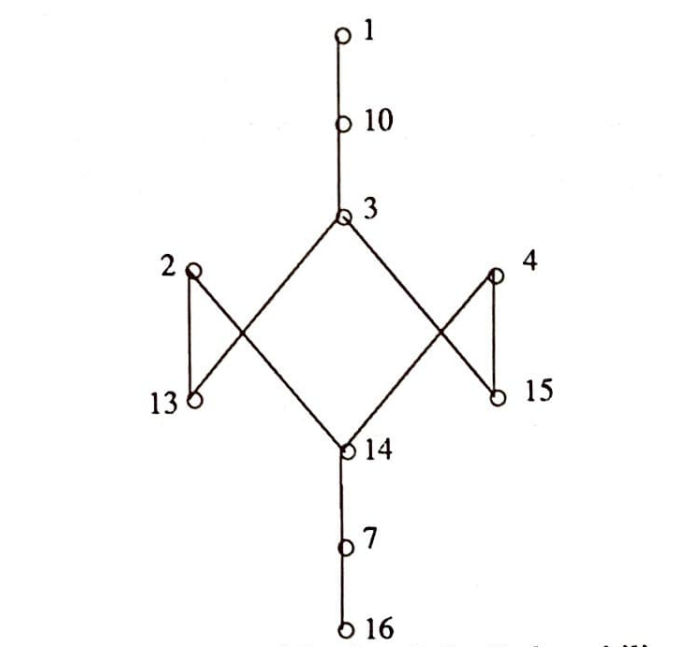
$T_1$ şeklinden de problemin çözümü okunabilir: birbirine eşdeğer (eş uzunlukta, en kısa) iki çözüm yolu vardır:
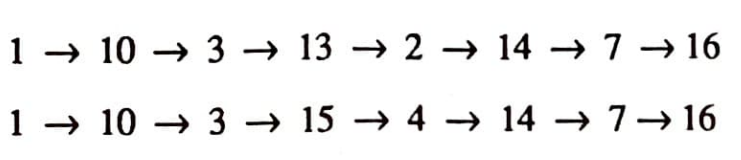
Çok bilinen bir başka problem de ‘üç ev – üç kuyu’ adıyla tanınan problemdir. Yapılması istenen, üç evi su alabilecekleri kuyulara birer patikayla bağlamaktır. Ancak kuyular zaman zaman kuruduğundan her evden her kuyuya bir patika bulunması gerekmektedir. Öte yandan, bu evlerde oturanlar arasında sebebi bilinmeyen bir çekişme vardır ve hiç kimse kendi yolunun kısmen de olsa diğer evlerde oturanlar tarafından kullanılmasını istememektedir.
Dikkat edilirse, problemin sunuluşunda evlerin ve kuyulann konumu hakkında hiç bir şey söylenmemektedir. Bunlan istediğimiz şekilde konumlandırabileceğimizi düşünebiliriz.
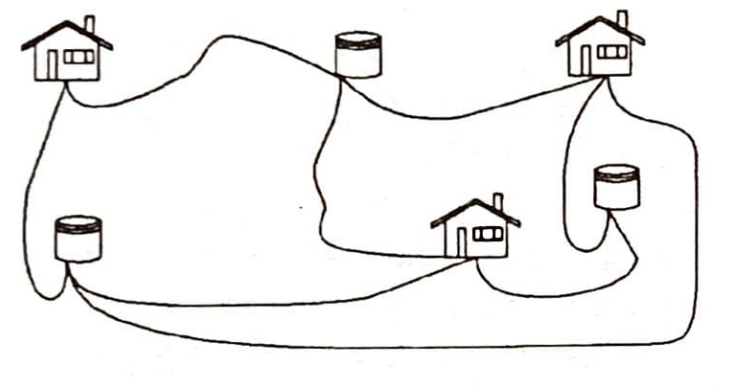
Bu problemle uğraşırken her defasında ev ve kuyu resimleri çizmemize gerek yoktur. Kuyuları beyaz (içi boş); evleri de siyah noktalarla gösterip, patikaları basit eğri parçaları olarak çizersek yukarıdaki şekil şu daha basit gelir:
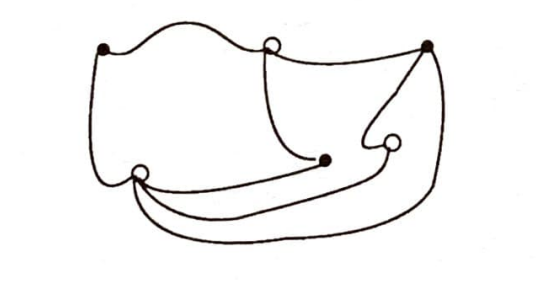
Yine düğümler ve kirişlerden oluşan bir şekil elde ettik. Son çizdiğimiz şekil, probleme bir çözüm getirmemektedir. Bu şekille uğraşmak yerine problemi en başından ele alalım. Patikaların kesişmesine aldırmadan, üç kuyuyu evlere bağlayarak problemi şöyle temsil edelim:
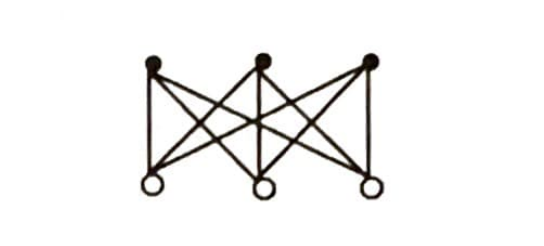
İleride anlaşılacak bazı sebeplerden bu şekle $K_{3,3}$ adını veriyoruz. Problemimizin son ifadesi şu; $K_{3,3}$ şeklini düzlemde, düğümlerin konumlarını ve kirişlerin şeklini değiştirerek, herhangi iki kiriş kesişmeyecek tarzda çizebilir miyiz? Evlere $A$, $B$, $C$ kuyulara da $1$, $2$, $3$ isimlerini vererek tekrar çizelim $K_{3,3}$ ü.
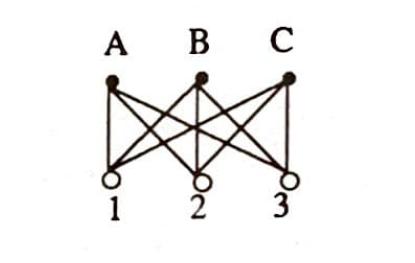
Düğüm ve kirişleri nasıl ve nerede çizersek çizelim, $(1, A)$, $(A,2)$, $(2,B)$, $(B,3)$, $(3,C)$ ve $(C,1)$ kirişleri ard arda gelecek ve ‘kapalı’ bir eğri tanımlayacaktır. Bu kapalı eğriyi şöyle çizelim:
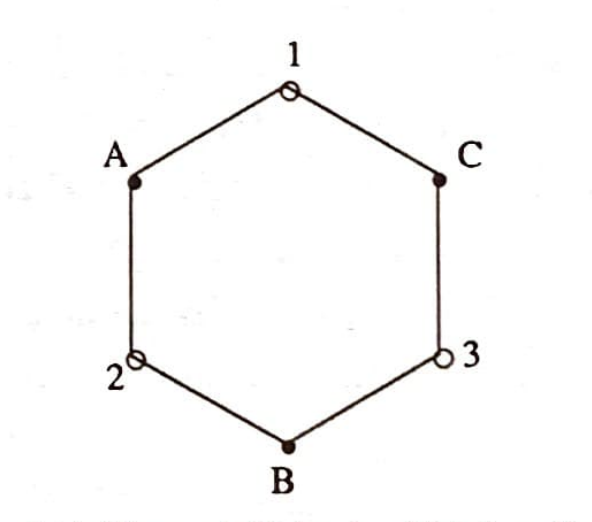
$K_{3,3}$ nasıl çizilirse çizilsin, bu kirişler dizisi daima bir kapalı eğri tanımlayacaktır. Bu sebeple, bu son elde edilen şekil problemin en genel haline denktir. Şimdi çizilmesi gereken üç kirişimiz daha var: $(A,3)$, $(B,1)$ ve $(C,2)$. Yukarıdaki kapalı eğri düzlemi iki kısıma ayırdı: iç bölge ve dış bölge. (Zaten ispatın özü de bu noktada toplanıyor. Kendisini kesmeyen ve kapalı her sürekli eğrinin düzlemi iki kısıma ayırması noktasında. Böyle eğrilere ait bundan başka özellikler de kullanacağız. Doğruluğunu kabul edeceğimiz bu özelliklerin ispatına girişmeyeceğiz.) Yeni çizilecek her kiriş bu kapalı eğrinin iki noktasını birleştirecektir. Bu kiriş eğer daha önce çizilmiş kirişleri kesmeyecekse (uç noktaları hariç) ya tamamen iç bölgede ya da tamamen dış bölgede yerleşmiş olacaktır. $(A,3)$ ve $(B, 1)$ kirişlerini ele alalım. Bunların ikisi birden içeriye veya ikisi birden dışarıya, birbirlerini kesmeden, çizilmez. Genellik bozulmadan $(A,3)$ ün içeride, $(B, 1)$ in de dışında olduğunu düşünebiliriz:
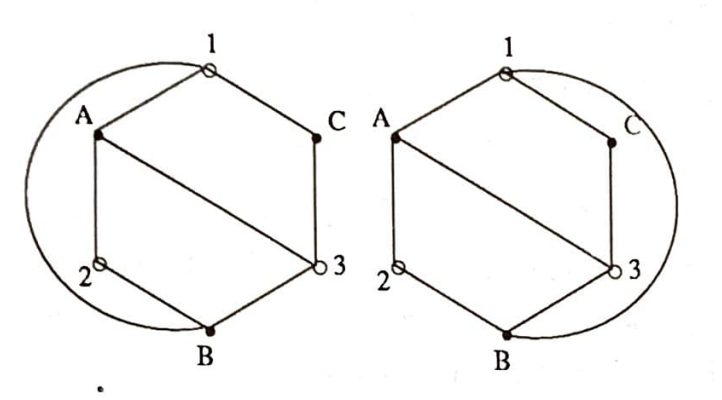
$K_{3,3}$ düzlemde $(C,2)$ kirişi ihmal edilerek çizildiğinde yukarıdaki iki şekilden birine (topolojik olarak) denk olacaktır. Sıra geldi $(C,2)$ kirişinin yerleştirilmesine. Her iki şekilde de $(B, 1)$, $(1,A)$, $(A,3)$, $(3,B)$ kirişlerinin kapalı bir eğri tanımladığını; birleştirilmesi gereken $2$ ve $C$ düğmelerinin birinin bu eğrinin iç bölgesinde diğerinin de dış bölgesinde kaldığını görüyoruz. Yani $(C,2)$ kirişinin daha önce çizilmiş bulunan kirişlerden birini kesmeden çizmek mümkün değildir. Böylece ‘üç ev – üç kuyu’ problemini istenen tarzda yollar çizilemeyeceğini göstererek çözmüş olduk.
Buraya kadar üç problem ele aldık: ‘Königsberg Köprüleri’, ‘Adam, Lahana, Kuzu, Kurt’ ve ‘Üç Ev-Üç Kuyu’ problemleri. Birbirinden çok farklı yapıdaki bu problemlere çözüm ararken kullandığımız ortak şey düğüm ve kirişlerden oluşan bir takım şekiller oldu. Böyle şekillere graf adı verilir. Bu yazımızda grafları tanımlayıp temel özelliklerini vermeye çalışacağız. Çok çeşitli sahalara uygulanma imkanı olan grafları inceleyen matematik kuramına Graf Teorisi adı verilmektedir. Bu teoriye ve uygulamalarına zaman zaman sayfalarımızda yer verip, hangi alanlarda nasıl kullanıldıklarını ve bunların kullanımıyla nasıl ilginç sonuçlara ulaşılabileceğini göstereceğiz.
Şimdiye kadar söylediklerimizi göz önüne alarak, bir grafın ne olduğunu ifade edelim. Düğüm adı verilen noktalar ve bunları birbirine bağlayan kiriş adını verdiğimiz eğri parçalarından oluşan bir şekle graf diyoruz. Düğüm yerine köşe veya tepe; kiriş yerine de yay veya dal da denmektedir. Kullanış amacımıza uygun olarak bütün düğümlerden oluşan $V$ ile bütün kirişlerden oluşan $E$ kümelerinin ayrı ayrı sonlu veya sonsuz olmasına izin verilebilir. Biz, en azından bu yazımızda, her iki kümenin de sonlu olmaları şartını koyacağız. Yani graf dediğimiz zaman daima düğümleri ve kirişleri sonlu sayıda olan bir graf anlayacağız. Bir grafta $V$ kümesinin boş olması çok anlamsızdır. Bu sebeple, $V$ nin her zaman en az bir elemanı olduğunu kabul edeceğiz. Öte yandan $E$ kümesi boş olabilir. Tanımlarımıza göre, bir $G$ grafının, birlikte düşünülen $V$ ve $E$ kümelerinden meydana geldiğini söyleyebiliriz. Yani, $V$ ve $E$ verildiğinde $G$ grafını $G(V,E)$ şeklinde yazabiliriz. Burada $V$, grafın düğümlerini; $E$ de bu düğümlerin nasıl bağlanacağını gösterir. $K_{3,3}$ örneğinde olduğu gibi, düzlemde çizilirken kirişlerin kesişmesinden kaçınamadığımız haller olabilir. Bu durumda düğümleri diğer kesişim noktalarından ayırdedecek şekilde çizmek gerekir. Bir grafın iki düğümü arasında hiç kiriş olmayabileceği gibi, bir kiriş veya daha fazla sayıda kiriş de olabilir. İki düğüm arasında en az bir kiriş varsa bunlara komşu düğümler; ortak bir düğümleri bulunan kirişlere de komşu kirişler deneceğini daha önce söylemiştik. Peki, bir düğüm kendisiyle komşu mudur? Eğer düğümü kendisine bağlayan bir kiriş varsa elbette bu düğüm kendisiyle komşu olur. Ama genel olarak, her düğüm kendisine doğal olarak komşudur diyemeyiz. Bir düğümü kendisine bağlayan bir kirişe, şeklinden dolayı, ilmek denir.
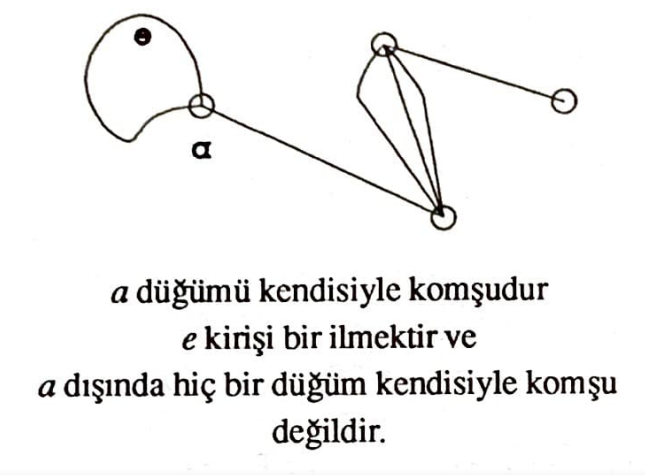
Bazı hallerde ilmeklerin bulunması veya iki düğümün birden çok kirişle bağlanmış olması sorun çıkarabilir. Bu haller için, sorun çıkamayan yani ilmeği ve iki düğümü arasında en çok bir kiriş bulunan graflarla sınırlı kalmak gerekir. Böyle gruplara basit graflar denir. Bazı kitaplarda graf tanımı doğrudan doğruya basit graf olarak verilir ve o zaman da iki düğümü arasında birden çok kiriş bulunan graflara özel bir isim verilir: multigraf.
Bir düğümdeki kirişlerin sayısına (yerel) derece diyoruz. Eğer $v$, bir $G$ grafının bir düğümü ise, $v$ deki derece $L(v)$ ile gösterilebilir. $L_{max}$ ve $L_{min}$ ile $G$ grafının derecelerinin içinde en büyüğü ve en küçüğü gösterilir. Bir $G$ grafında düğümleri saymak kolaydır, ancak kirişleri tek tek saymaya kalkışırsak işimiz çok kolay olmayabilir. Örneğin aşağıdaki grafta düğümler 7 tanedir ama kirişleri saymaya kalkışmak pek akıllıca görünmüyor.
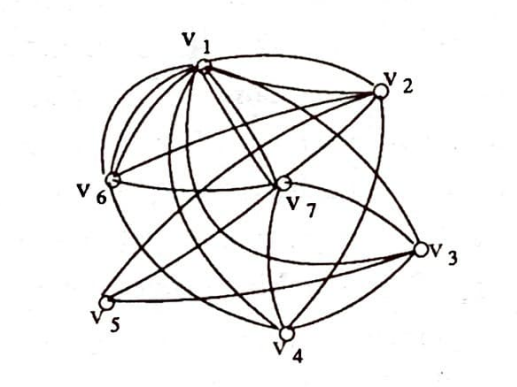
Fakat şunu biliyoruz ki her kirişin iki ucu vardır ve bu uçların her biri bir düğüme bağlanmıştır. Her düğümdeki kirişlerin sayısını toplarsak, bütün kirişleri ikişer kez saymış oluyoruz. Yani, bütün düğümlerdeki derecelerin toplamı, kiriş sayısının iki katına eşittir. Bunu şöyle yazabiliriz:
Bir $G$ grafında $n$ düğüm ve $e$ kenar bulunsun.
Düğümler kümesi
$$V=\{v_1,\dots,v_n\}\quad ise\quad 2e=\sum_{i=1}^n L(v_i)\quad olur.$$
Bunu yukarıdaki grafa uygularsak
$$L(v_1)=10, L(v_2)=6,L(v_3)= 5, L(v_4) =5, L(v_5)= 3, L(v_6)= 6 ve L(v_7) =7$$
olduğundan $2e=10 + 6 + 5 + 5 + 3 + 6 + 7=42 \implies e= 21$ elde edilir. Bütün lokal dereceleri aynı olan graflara düzgün (regüler) graflar denir. Lokal dereceler hep $r$ ise graftan, r-li düzgün graf olarak bahsedilir. $|V| =n$ olan bir r-li düzgün grafta $|E|=e=\frac{1}{2}nr$ olacağı açıkça görülür. Aşağıda 6 şar noktalı 3-lü düzgün graflara iki ömek verilmiştir:
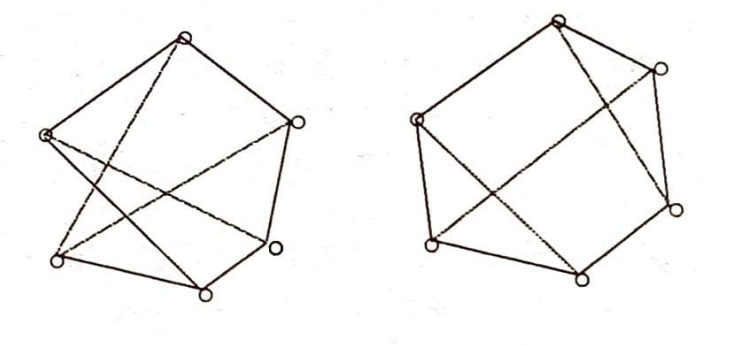
$K_{3,3}$ de düzgün graftır. Tek sayıda düğümü olan bir graf r-li düzgün ise r-nin çift olması gerektiğini görüyoruz. Yani, söz gelimi, 7 noktalı bir 3-lü düzgün graf yoktur. Daha genel olarak $n$ düğümlü bir r-li düzgün graf için $r$ ve $n$ nin en az biri çift olmalıdır.
Bir grafta derecelerin toplamının, kiriş sayısının iki katı olduğunu gösterdik. Yani $L(v_1)+L(v_2)+\dots+L(v_n)$ toplamı her zaman çift bir sayıdır. Tek sayıda tek sayının toplamı yine tek sayı olduğundan, yukarıdaki toplamda yer alan tek sayıların çift sayıda olması gerektiği anlaşılır.
Yani, bir grafta derecesi tek olan olan düğümlerin sayısı çift olmak zorundadır. Bunu teorem olarak yazabiliriz :
TEOREM 1. Her grafta, derecesi tek olan düğümlerin sayısı çifttir.
Şu ana kadar, dünya üzerinde yaşamış olan bütün insanları düşünelim. Her insan ömrü boyunca diğer insanlarla zaman zaman el sıkışmaktadır. Elbette hiç kimse kaç kere el sıkışmış olduğunu bilemez. Hatta çift sayıda veya tek sayıda el sıkışmış olduğunu dahi bilemez. Ancak, yukarıdaki teoremimizi kullanarak, şu ana kadar yaşamış olan insanların içinde tek sayıda el sıkışmış olanların sayısının çift olduğu sonucuna varırız.
Bir grafta yalnız başına kalmış düğümler bulunabilir. Yani, ne kendisine ne de başka düğümlere komşu olmayan düğümler bulunabilir. Diğer düğümlere küsmüş böyle düğümlere izole düğümler denir. Aşağıdaki grafta a düğümü bir izole düğümdür.
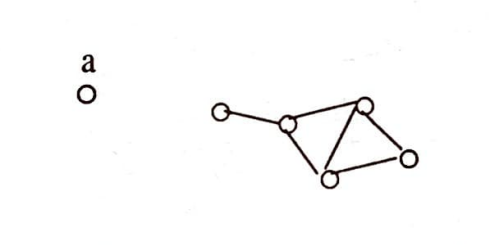
Bütün düğümleri izole olan bir grafa da boş graf adı verilir. Dikkat edilirse bir grafın boş olması kirişler kümesi $E$’nin boş olması manasını taşımaktadır. $n$ düğümlü boş graf $O_n$ ile gösterilir.

Bir grafın düğüm kümesinin boş olmasına izin vermiyoruz. Buna izin verseydik, $V=\emptyset$ olduğunda $E=\emptyset$ olması da kaçınılmaz olacaktı. O zaman da böyle bir grafa (boş olmasından da öteye), bomboş graf diyecektik.
Bir yanda hiç kirişi olmayan graflar varken, diğer yanda da bütün düğümleri birbirine bağlı graflar vardır. Herhangi iki düğümü komşu olan basit graflara tam graf denilmektedir. Yani bir tam graf, iki düğümü arasında en fazla bir kiriş olması ve hiç ilmek bulunmaması şartları ile mümkün olan en çok sayıda kirişle donatılmış graftır. Düğüm sayısı $n$ olan bir tam graf $K_n$ ile gösterilir.
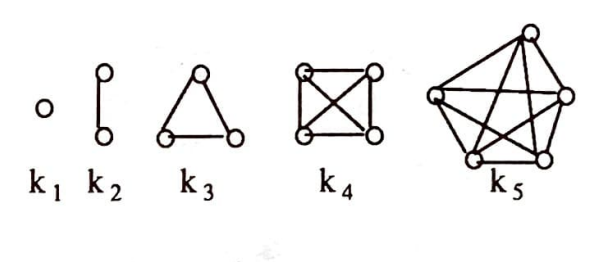
$K_n$ grafı tabi olarak $(n-1)$-li düzgün graftır ve $\frac{1}{2}(n-1)$ kirişe sahiptir.
Bazı graflarda düğüm kümesi boş olmayan öyle alt kümelere parçalanabilir ki, her bir parçaya düşen düğümler kendi aralarında komşu olmazlar. Ömeğin aşağıdaki $G$ grafını ele alalım.
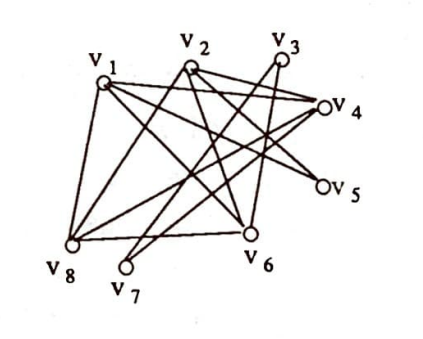
Görülüyor ki, $\{v_1,v_2,v_3\},\{v_1,v_5, v_2\}$ ve $\{v_1,v_8\}$ kümelerinde yer alan düğümler kendi aralarında komşu değildir. Bir grafın düğüm kümesi bu şekilde parçalanabiliyorsa ve bu parçalanmalar için en az t küme gerekiyorsa grafa t-parçalı denir. Örneğin, yukarıdaki $G$ grafı için bir başka parçalanma $ \{v_1, v_3\},\{v_2, v_5\}, \{v_4, v_8\},\{v_4, v_6\}$ dir ama bu halde parçalamayı 4 küme ile yaptık. G kümesi bu şekilde parçalandığında en az 3 altküme kullanmak gerekir, yani $G$, 3-parçalıdır. İki parçalı ve mümkün olan en fazla sayıda kirişi olan bir basit grafa 2-parçalı tam graf denir, ve böyle bir graf $K_{p,q}$ ile gösterilir. Burada $p$ ve $q$ düğüm kümesinin parçalandığı kümelerin düğüm sayıları dır. O halde $K_{p,q}$ öyle bir graftır ki, bir tarafta $p$ tane; diğer tarafta da $q$ tane düğüm bulunmaktadır. İki düğüm eğer aynı taraftaysa aralannda kiriş yoktur, eğer ayrı taraftalarsa aralarında tam bir tane kiriş vardır. Tanımlardan anlaşıldığı üzere $K_{3,3}$ bir 2-parçalı tam graftır.
Bazı 2-parçalı tam graflar:
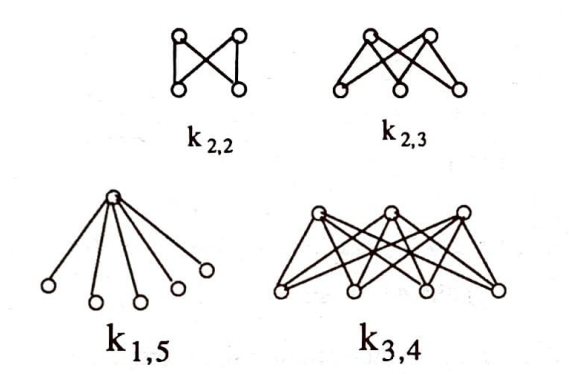
$K_{p,q}$ grafında düğüm sayısı $p + q$ olacaktır. Kiriş sayısının $pq$ olduğu da hemen gösterilebilir.
(Kiriş Dizileri)
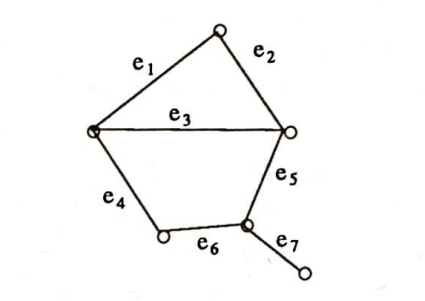
Bir G grafında kirişlerden meydana gelen sıralanmış bir diziyi göz önüne alalım. Ömeğin aşağıdaki $G$ grafı için $e_1$ $e_3$ $e_7$ $e_6$ $e_3$ böyle bir sıralanmış dizidir. Eğer ardışık kenarların bir onak ucu varsa böyle bir diziye “gezinti” denir. Ömeğin $e_1$ $e_3$ $e_5$ $e_6$ $e_4$ $e_3$ bir gezintidir. Bu gezintide $e_3$ kirişi iki kere kullanılmaktadır.
Böyle bir halin olmadığı, yani bir kirişin en fazla bir kere kullanıldığı gezintilere dolaşım diyoruz. Yukandaki grafta $e_3$ $e_2$ $e_1$ $e_4$ $e_6$ $e_5$ bir dolaşımdır. Bu sefer her 1 kiriş bir kez kullanıldı fakat bazı düğümler iki defa ziyaret edildi. Buna da izin verilmezse; yani her düğüm en fazla bir kez ziyaret edilirse dolaşıma yol diyoruz. Bir gezinti veya dolaşım başladığı noktada biterse kapalı olarak nitelendirilir. Bir yolda her düğüm bir kereden fazla kullanılamıyordu. Hareketin başlangıç noktasında bitirilebilmesi amacıyla bir istisna yapılırsa ortaya bir kapalı yol veya devre çıkar. Kapalı dolaşıma Euler dolaşımı da denmektedir. Bir grafta bütün kirişlerin ve düğümlerin kullanıldığı bir Euler dolaşımı varsa yani grafın kendisi bir Euler dolaşımı ise, grafa bir Euler grafı deriz.
Her hangi iki düğümü arasında bir yol bulunan graflara bağlantılı graflar denir. Bağlantılı olmayan graflara bir ömek, izole düğümleri olan bir graftır. Aşağıdaki graf da bağlantısız bir graftır. Bağlantısız bir grafta, bağlantılı olan maksimal parçalara grafın bileşenleri denir.
Bileşenlerin sayısını da $c$ ile gösteriyoruz. Böylece, bağlantılı bir grafta $c=1$ olur.
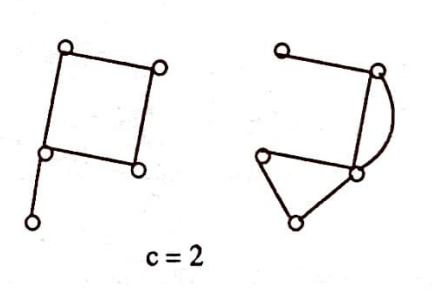
Königsberg köprüleri problemine geri dönüyoruz. Buraya kadar geliştirdiğimiz terminolojiyle problemi şöyle ifade edebiliriz. Aşağıda verilen graf Euler grafı mıdır?
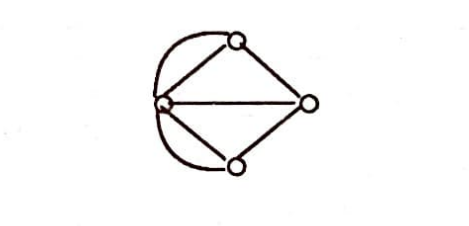
Problemi tartışırken vardığımız sonuç, bir grafın Euler grafi olabilmesi için bütün düğümlerinin çift dereceli olması gerektiği idi. Bu şart aynı zamanda yeter şarttır.
TEOREM: Bağlantılı bir grafın Euler grafı olabilmesi için gerek ve yeter şart bütün düğümlerdeki derecelerin çift olmasıdır.
TEOREM: Bağlantılı bir grafta sadece iki düğüm tek dereceli; diğerleri çift dereceli ise, tek dereceli düğümlerin birinden başlayıp diğerinde bitecek şekilde bir dolaşım vardır.
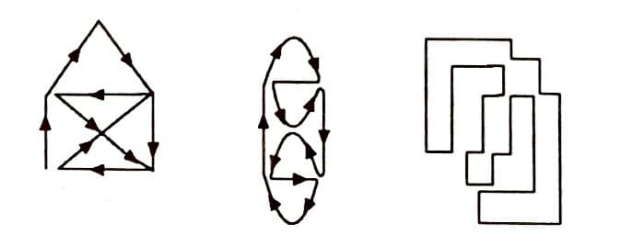
Bu teoremler yardımı ile düzlemde verilen bir şeklin, kalem kağıttan kaldırılmadan ve çizilen çizgilerin üzerinden gitmeden çizilip, çizilmeyeceği tayin edilebilir. Aşağıda verilen şekilleri ele alalım.
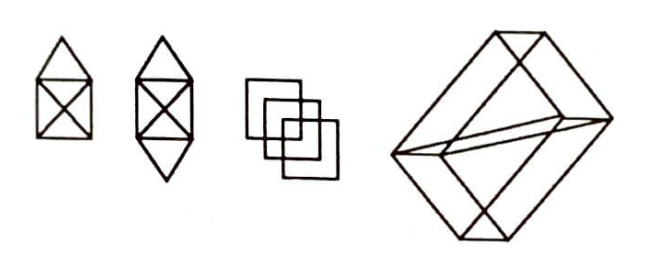
Bu şekillerden hangilerini kalemi kağıttan kaldırmadan ve çizdiğimiz çizgilerden tekrar geçmeden çizebiliriz? Önce bu şekilleri, düğüm ve kirişler daha belirgin olacak şekilde tekrar çiziyoruz.
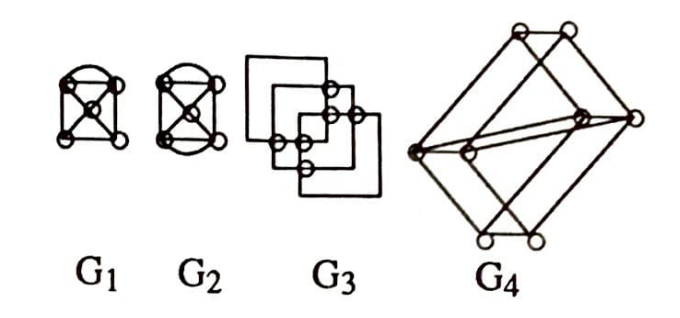
$G_1$-de tek dereceli iki düğüm vardır. Bunların birisinden başlayıp diğerinde duracak şekilde, bu şekil çizilebilir $G_2$ ve $G_3$ -de bütün düğümler çift dereceli olduğundan, her iki şekilde her hangi bir noktadan başlayıp, yine orda duracak şekilde çizilebilir. $G_4$ de ise tek dereceli dört düğüm olduğundan bu şekil çizilemez.
Devamı sayı 2’de
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1993 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Eren‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

