Yıl: 1993-1
Yazar: Cem Tezer
Konumuzu teşkil eden çemberleri bugün adıyla anmakta olduğumuz Gianfrancesco Malfatti (1737-1807) Ferrara Üniversite’sinde (Kuzey İtalya) fizik profesöıü olarak çalışırken 1803 yılında yazdığı ([6]) bir makalede şu ilginç problemi ortaya atmış:
“Herhangi bir maddeden, mesela, mermerden yapılmış bir üçgen dik prizmadan en az malzeme ziyan olacak şekilde üç dairesel dik silindir nasıl çıkarılır?”
Tabii ki bu üç boyutlu sunuş aslında gereksiz. Prizma yerine, onun eksenine dik bir düzlem üzerine dik izdüşümü olan üçgen, silindir yerine de gene aynı şekilde elde edilmiş bir çember alınabilir. O zaman problem, verilen bir üçgen içine alanları toplamı en büyük olacak şekilde birbirinin “üzerine çıkmayan” üç çemberin nasıl yerleştirileceği problemidir.
Bu eski ve elde edilmesi güç makaleyi ben de görmediğim için, Malfatti’nin bu problem üzerindeki çalışmaları hakkında fazla bir şey söyleyemeyeceğim. Kaynağı görenlerin, okuyanların (mesela [3], [5], [1], [2] gibi) yalancısı olduğumu belirterek bu hususta bildiğim birkaç şeyi nakledeyim: Malfatti, söz konusu problemi yukarda işaret ettiğimiz gibi bir düzlem geometri problemi haline getirdikten sonra, çözümün aşikar olarak , (Şekil 1 de $\gamma_a,\gamma_b,\gamma_c$ ile gösterilen) her biri diğer ikisine dıştan, gene her biri üçgenin ilgili iki kenarına içten teğet çemberlerden ibaret olduğunu belirtiyor. Malfatti, bu çemberlerin, üçgenin içinde nasıl bir konuma sahip olduklarını anlamak maksadıyla bazı hesaplar da yaparak, sonuçta işte bugün Malfatti çemberleri olarak andığımız, bu yazıda bir yüzyılı geçen maceralarından birkaç safhayı nakledeceğimiz çemberleri matematik dünyasına kazandırıyor.
Az evvel söylediğim gibi Malfatti’nin hesaplarını bilmiyorum. Buna karşılık çağdaş kaynaklarda az tanınmış bir matematikçi ([2] , [5]) olan Schellbach’a izafe edilen bazı ilginç hesapları okuyucuya aktarmak istiyorum. Bu hesapların dikkate değer tarafı, küçük bir gözlemle Malfatti çemberlerinin pergel ve cetvelle çizilebilir olduğunu ispat edebilmeleridir.
Her zamanki gibi bir $ABC$ üçgenine bağlı olarak, $a=|BC|, b=|CA|,c=|AB|$ ve $2s=a+b+c$ yazalım. $ABC$’nin içteğet çember yarıçapı $r$ olsun. Malfatti dokusuna ait birkaç gösterimi de Şekil 1 yardımıyla sunalım: $\gamma_a,\gamma_b,\gamma_c$ çemberlerinin yarıçapları sırasıyla $\rho_a,\rho_b,\rho_c$; $BC,CA,AB$’ye teğet oldukları noktalar da $A_1$ ve $A_2$, $B_1$ ve $B_2$, $C_1$ ve $C_2$ olsun. Ayrıca (bu hesaplarda değil ama sonradan kullanılmak üzere) $\gamma_b$ ve $\gamma_c$, $\gamma_c$ ve $\gamma_a$, $\gamma_a$ ve $\gamma_b$’nin birbirlerine sırasıyla $P, Q, R$ noktalarında değdiklerini farz edelim. Nihayet
$$|AB_2|=|AC_1|=u, \quad |BC_2|=|BA_1|=v, \quad |CA_2|=|CB_1|=w$$
yazalım. Malfatti çemberlerinin üçgen içindeki konumunu bilmek için $u, v, w$ miktarlarını $a,b,c$ cinsinden hesaplamak tabii ki yeterlidir.
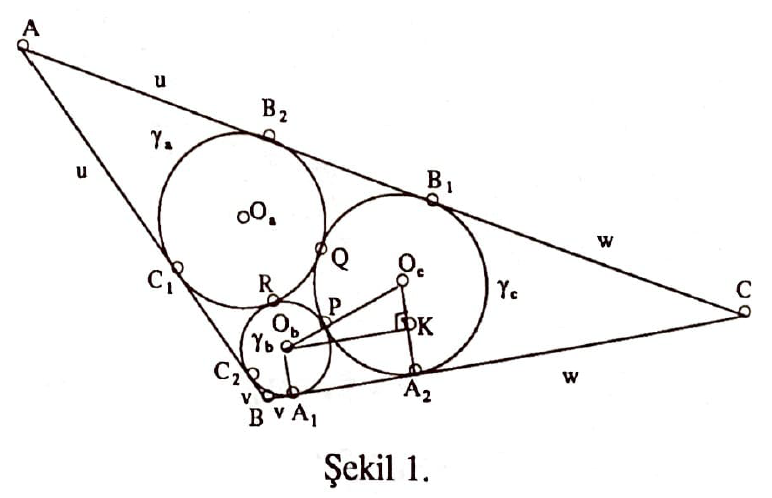
$O$’den $O_cA_2$’ye indirilen dikmenin ayağına $K$ dersek, $O_cO_bK$ dik üçgeninde Pisagor teoreminden,
$$|A_1A_2|^2=|O_bO_c|^2-|O_cK|^2=(\rho_b+\rho_c)^2-(\rho_c-\rho_b)^2=4\rho_b\rho_c$$
yani
$$|A_1A_2|=2\sqrt{\rho_b\rho_c}$$
bulunur. Diğer taraftan
$$\frac{\rho_b}{v}=\frac{r}{s-b}$$
$$\frac{\rho_c}{w}=\frac{r}{s-c}$$
olduğundan
$$|A_1A_2|=2\sqrt{\rho_b\rho_c}=\frac{r\sqrt{vw}}{\sqrt{(s-b)(s-c)}}$$
ve ($ABC$’nin alanını $\Delta$ ile gösterirsek)
$$sr=\Delta=\sqrt{s(s-a)(s-b)(s-c)}$$
den
$$|A_1A_2|=2\sqrt{\frac{s-a}{s}}\sqrt{vw}$$
bulunur. $|AB_1|+|A_1A_2|+|A_2C|=a$ olduğundan
$$v+w+2\sqrt{\frac{s-a}{s}}=a\qquad (1)$$
benzer şekilde de
$$w+u+2\sqrt{\frac{s-a}{s}}=b \qquad (2)$$
$$u+v+2\sqrt{\frac{s-a}{s}}=c\qquad (3)$$
elde edilir. Buraya kadar herkesin yapabileceği bir hesabı yürüttük. Şimdi zarif nokta:
$$\sin \xi=\sqrt{\frac{u}{s}}\quad \sin \alpha=\sqrt{\frac{a}{s}}$$
$$\sin \eta=\sqrt{\frac{v}{s}}\quad \sin \beta=\sqrt{\frac{b}{s}}$$
$$\sin \zeta=\sqrt{\frac{w}{s}}\quad \sin \gamma=\sqrt{\frac{c}{s}}$$
şeklinde $\alpha,\beta,\gamma,\xi,\eta,\zeta$ açı-miktarlarını ithal edersek (1),(2),(3) denklemleri
$\sin^2\eta+\sin^2\zeta+2\sin\eta\sin\zeta\cos\alpha=\sin^2\alpha\qquad (4)$
$\sin^2\zeta+\sin^2\xi+2\sin\zeta\sin\xi\cos\beta=\sin^2\beta\qquad (5)$
$\sin^2\xi+\sin^2\eta+2\sin\xi\sin\eta\cos\gamma=\sin^2\gamma\qquad (6)$
şeklini alır. Üçgende kosinüs teoremi hatırlanırsa bu denklemlerin sağlanması için yeter şart olarak
$\eta+\xi=\alpha\qquad (7)$
$\zeta+\xi=\beta\qquad (8)$
$\eta+\xi=\gamma\qquad (9)$
alınabilir. Demek ki $2\sigma=\alpha+\beta+\gamma$ olmak üzere (7),(8),(9) denklemlerinden
$\xi=\sigma-\alpha$
$\eta=\sigma-\beta$
$\zeta=\sigma-\gamma$
yazarsak,
$u=s\sin^2\xi$
$v=s\sin^2\eta$
$w=s\sin^2\zeta$
çıkar. Bilinen $a, b, c$ uzunluklarından $s, \alpha,\beta,\gamma$, bunlardan da $\xi,\eta,\zeta$ ve en nihayet $u, v, w$ miktarları açık bir şekilde pergel ve cetvelle elde edilebilir. Demek ki Malfatti çemberleri pergel ve cetvelle çizilebilmektedir.
Bu bilgi önemli olmakla birlikte geometriseveri tatmin etmeyecektir. Malfatti’nin makalesinin hemen ardından, matematikçiler hesaba değil, doğrudan geometriye bağlı bir çizimi heyecanla aramış. Herkesi tatmin eden teorem J. Steiner’e ait:
Teorem: ([7], 1826) $ABC$ üçgeninin içteğet çemberinin merkezi $I$; $CIA, AIB$ üçgenlerinin içteğet çemberleri $\Gamma_b,\Gamma_c$ olsun. $\Gamma_b,\Gamma_c$’nin $AI$ doğrusu olmayan iç ortak teğeti aynı zamanda $\gamma_b,\gamma_c$ Malfatti çemberlerinin de ortak teğetidir. (Şekil 2a,b).
Bu teoremin geometri meraklısında yarattığı, eşit miktarlarda şaşkınlık, hayranlık, vecd ve isyan hislerinin karışımı ruh hali, Steiner’in birçok başka eserinden de edinilebilir. Bu teoremi daha da dikkate değer hale getiren husus, Steiner’in onu (herhalde çağdaşı geometricileri çileden çıkartmak için) ispatını vermeden yayınlamış olması. Yıllarca birçok matematikçi bu teoremi ispat etmeye çalışmış. J.L. Coolidge’e [1] göre ilk ispat Hart adında az tanınmış bir İngiliz geometrici tarafından verilmiş. Bu ispat, matematik dünyasında, Hart’ın Steiner’ın zamanında bilinmeyen bir teknik (yani evirtim) kullandığı gerekçesiyle pek “hüsn-i kabul” görmemiş. J.L. Coolidge bu durumdan, bugün pek yakışık veremediğimiz bir “gayret-i milliyet” ile (herhalde biraz daha Birinci Dünya Savaşı’ndan hemen önceki yılların gerginliği içinde) “Eğer Hart, Steiner’ın milletinden olsaydı, işler başka türlü olurdu!” diye yakınır. Her neyse… Okuyucu Steiner’ın meçhul ispatının matematikçilere ne kadar dert olduğunu iyice anlamıştır herhalde. Ben Hart’ın Coolidge tarafından nakledilen ispatını, yazıyı yetiştirmek telaşından pek okuyamadım. Yıllarca evvel eski ve şimdi tam hatırlayamadığım bir geometri kitabında okuyup, anlayamayıp, sonra kendimce birkaç ilave ile elde ettiğim, evirtime dayalı bir ispatı sunmak istiyorum. Steiner’ın böyle düşündüğü yolunda bir iddiam da hiç yok!
İspat: (Şekil 2a, 2b, 2c)
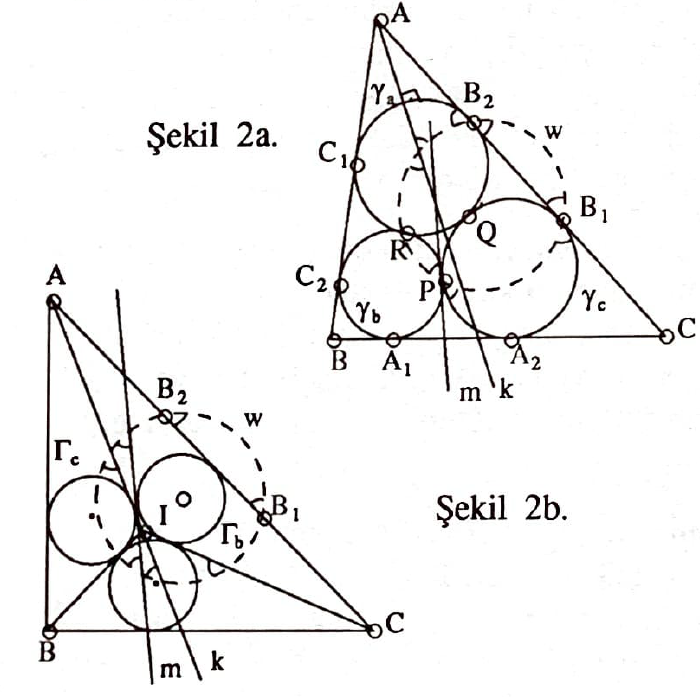
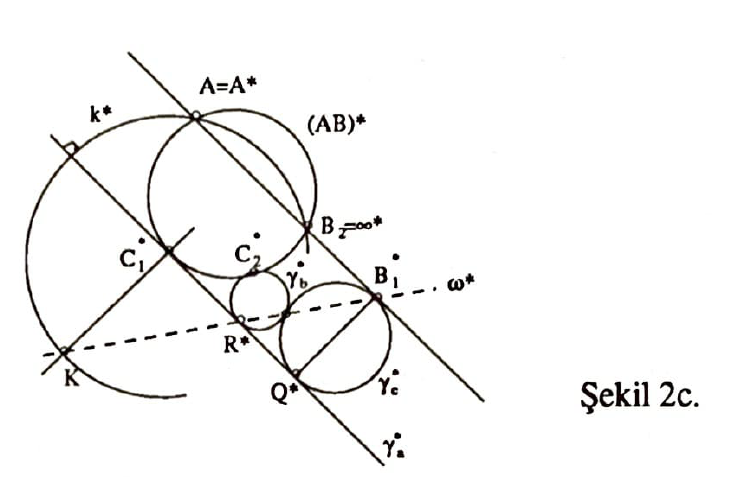
Önce $B_1, B_2, P, R$ noktalarının çemberdeş olduklarını hatırlatalım. (Mesela, Problem 1, [8]). Bu noktaların üzerinde kaldığı çember $\omega$ olsun, $B_2$ noktası merkez olmak üzere bir evirtim göz önüne alalım. Herhangi bir geometrik şey $X$’in bu evirtim altındaki görüntüsünü $X^*$ ile gösterelim; $A$ açısının içaçıortayını $k$ ile; $\gamma_b$, $\gamma_c$’nin ortak teğetini $m$ ile gösterelim. İspatımızın ağırlık noktası $k$ ile $\omega$ arasındaki açının, $AC$ ile $\omega$ arasındaki açıya eşit olduğunu göstermek (Şekil 2a). Bunu yapabilirsek, $AC$ ile $\omega$ arasındaki açı $m$ ile $\omega$ arasındaki açıya eşit olduğundan (bütün bu münakaşayı bir de $C$ açısının açıortayı için tekrarlayarak!) $CI, AI=k, m$ ve $AC$ doğrularının $\omega$ çemberinin merkezine eşuzaklıklı olduklarını, bu suretle de $\omega$ ve $\Gamma_b$’nin eşmerkezli olduklarını ve en nihayet hem $k$, hem de $m$’nin $\Gamma_b$’ye teğet olduklarını göreceğiz (Şekil 2b). Aynı münakaşayı bir de $ABI$ için tekrarlayarak $m$’nin $\Gamma_b$’ye de teğet olduğu görülebilir, ispat biter.
Böylece yapmamız gereken tek şey olarak $k$ ile $\omega$ arasındaki açının $\omega$ ile $AC$ arasındaki açıya eşitliğini göstermek kalıyor. Evrik şekle geçelim (Şekil 2c): $AB$ doğrusunun evriği olan $(AB)^*$ çemberinin yarıçapı $r_1$ sırasıyla $\gamma_b^*,\gamma_c^*$ çemberlerinin yarıçapları da $r_2,r_3$ olsun. Küçük bir hesapla
$|C_1^*A|=2\sqrt{r_1r_3}$
$|Q^*R^*|=2\sqrt{r_2r_3}$
$|R^*C_1^*|=2\sqrt{r_1r_2}$
bulunur. $\omega^*$’in $C_1^*$’dan $\gamma_a^*$’a çizilen dikmeyi kestiği nokta $K$ olsun. $KC_1^*R^*$ ve $B_1^*Q^*R^*$ dik üçgenlerinin benzerliğinden $|KC_1^*|:|R^*C_1^*|=|B_1^*Q^*|:|Q^*R^*|$ olup, buradan
$|KC_1^*|=\frac{|B_1^*Q^*||R^*C_1^*|}{|Q^*R^*|}=2\sqrt{r_1r_3}$
bulunur. Demek ki $|KC_1^*|=|C_1^*A|$’dır. O zaman $C_1^*$ merkezli |C_1^*K| yarıçaplı çember $A$’dan geçmelidir. Bu çember $\gamma_a^*$’a dik olacağından ancak $k^*$, yani $A$ açısının içaçıortayı $k$ doğrusunun evriği olabilir. $K$’dan $k^*$’a çizilen teğet $\gamma_a^*$’a, dolayısıyla $AB_1^*$’a paralel olduğundan, $\omega^*$’la $k^*$ arasındaki açıya eşittir. Sonuç olarak $\omega$ ile $k$ arasındaki açı da $AB_1=AC$ ile $\omega$ arasındaki açıya eşit olmalıdır.
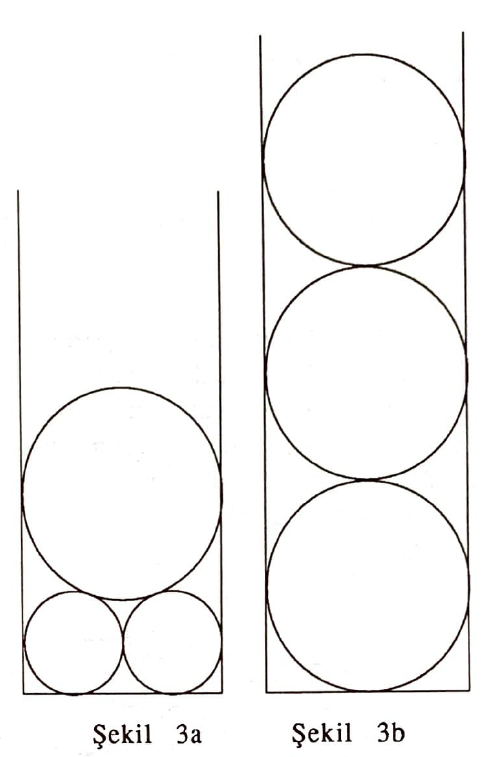
Yazımızı, Malfatti çemberlerinin meydana getirdiği harikulade dokuyla daha yeni tanışmış okuyucumuzu biraz üzerek bitirelim. Ne yazık ki Malfatti çemberleri, asıl Malfatti probleminin çözümü değildir. Hatırlayalım: Malfatti problemi bir üçgenin içine birbirinin üzerine çıkmadan yerleşip, mümkün olan en geniş alan kaplayan üç çember istiyor. G. Malfatti bu işin “aşikar olarak” Malfatti çemberleri tarafından yapıldığını söyleyip bırakmış. Bir ispat yok! Böyle bir ispatın olmadığının ilk farkına varanlar H.Lob ve H.W. Richmond [5]. Nedense bu işe uzun ve ayrıntılı makalelerinin en son cümlesinde, o da pek mütereddit bir ifadeyle, temas ediyorlar. Halbuki durum gerçekten şaşırtıcı: Malfatti çemberlerinin asıl Malfatti problemine hiçbir zaman çözüm teşkil etmediği 1967’de M. Goldberg tarafından gösterilmiştir. Okuyucu için en güzel örnek tepesi “sonsuzda” yani taban açılan doksanar derece olan bir ikizkenar üçgende Malfatti çemberlerinin toplam alanıyla (Şekil 3a) Şekil 3b’deki çemberlerin toplam alanını karşılaştırmak olacaktır.
Kaynaklar:
[1] J.L. Coolidge: “A Treatise on the Circle and the Sphere” Chelsea Publishing Company, New York 1971. (İlk basım: Oxford, 1916)
[2] H. Dörrie: “100 Great Problems of Elementary Mathematics, Their History and Solution” Almanca’dan çeviren D. Antin, Dover Publications, New York 1965.
[3] H. Eves: “A Survey of Geomery” Allyn and Bacon, Boston 1963.
[4] M. Goldberg: “The original Malfatti Problem” Mathematics Magazine, 40 (1967) 241-247.
[5] H.Lob, H.W. Richmond: “On the solutions of Malfatti’s problem for a triangle” Proceedings of the London Mathematical Society 30 (1930) 287-304.
[6] G. Malfatti: “Memoria sopra un problema sterotomica” Memorie di Matematica e di Fisica della Societâ İtaliana delic Szienze 10 (1803) 235-244.
[7] J. Steiner: “Einige geometrische Betrachtungen” Creııe’s Journaı ı (1826) 161-184, 252-258. Ben bu yazıyı Steiner’ın bütün eserlerinin toplandığı bir kitapta okudum: “Gesammelte Werke” Cilt I, Sayfa 19-76, Chelsea Publishing Company, Bronx, New York 1971, (İlk basım: Berlin 1881).
[8] C.Tezcr: “Evirtim” Matematik Dünyası, Cilt 2 Sayı 1, Sayfa 12-16.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1993 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Övünç Özgür Eker‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

