Yıl: 1994-1
Yazar: Şafak Alpay
Ünlü Moskova Devlet Üniversitesi’nin işlevini yerine getiremediği düşüncesi ile bazı Moskovalı matematikçiler Bağımsız Moskova Üniversitesi’ne bağlı olarak kurulan Matematik Koleji ile gelecekteki araştırmacıları yetiştirmek için yeni bir okul kurdular. Kurucuları V.I. Arnold ve N.N. Konstantinov olan okul aşağıda sorularını verdiğimiz sınavla Eylül 1991’de sayıları 45 olan ilk öğrencilerini seçti. Haziran 1991 tarihinde yapılan sınav 120 üzerinden değerlendirildi.
Giriş Sınav
1. Gerçel $x$ ve $y$ için $f(x)-f(y) \leq (x-y)^2$ eşitsizliğini sağlayan tüm $f$ fonksiyonlarını bulunuz.
2. $x^{2n}-2x^{2n-1}+3x^{2n-2} \cdots \cdots 2nx+2n+1$ çokterimlisinin gerçel kökü olmadığını gösteriniz.
3. $2^{2^{n}}+2^{2^{n-1}}+1$ sayısının asal çarpanlarını sayısının $n$’den küçük olmadığını gösteriniz. (Asal çarpanlar farklı olmayabilir.)
4. Düzgün bir tetrahedronun içine ve dışına çizilen kürelerin hacimlerinin oranını bulunuz.
5. Bir $ABC$ üçgeninin tüm açılarının dar açı olması için gerekli ve yeterli koşulun, $AB$,$AC$ ve $BC$ kenarları üzerinde $AA^{\prime}$, $BB^{\prime}$ ve $CC^{\prime}$’nin eşit uzunlukta olduğu $A^{\prime}$, $B^{\prime}$ ve $C^{\prime}$ noktalarının varlığı olduğunu kanıtlayınız.
6. $a_1, a_2, \cdots \cdots ,a_{100}$ dizisi $1,2,\cdots,100$ sayılarının bir permütasyon olsun. $1.a_1+2.a_2+\cdots + 100.a_{100}$ toplamının minimum değerinin $100,99,\cdots,1$ permütasyon için alındığını gösteriniz.
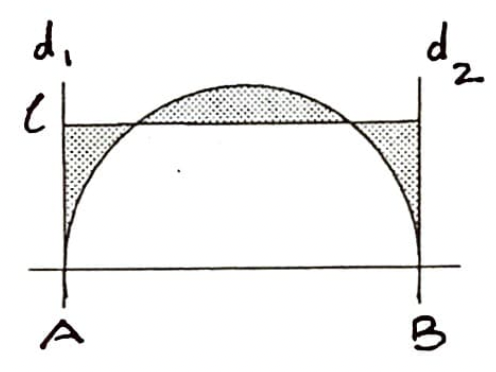
7. Şeklinde, $AB$ verilen dairenin yarıçapı, $d_1$ ve $d_2$, $A$ ve $B$ noktalarından çizilen teğetler ise taralı alanın minimum olacağı $l$ doğrusunu bulunuz.
8. $L_1$ ve $L_2$, çevresi $L$ olan dairenin içine ve dışına çizilen düzgün $n-$genlerin çevresi olsun. $S$ dairenin, $S_1,S_2$ çokgenlerin alanları ise
$$a) L^2<L_1L_2$$
$$b)S_1S_2<S^2$$
olduğunu gösteriniz.
9. Bir üçgenin kenar uzunlukları oranın alabileceği sayılar neler olabilir?
10. Her alt dizisinin periyodik olmayan bir aritmetik altdizisi olan, $0$ ve $1$’lerden oluşmuş bir dizi var mıdır?
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Emre Kahvecioğlu‘na ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

