Yazar: Alparslan Ertuğ
Yıl: 1994-2
Geometri problemleri çözülürken genellikle üç temel yöntem kullanılır: Geometrik, cebirsel ve birleşik yöntem. Geometrik yöntem, bilinen bir dizi teoremden mantıksal önermeler yardımıyla istenen ifadenin çıkarılmasıdır. Cebirsel yöntem ise geometrik büyüklükler arasındaki çeşitli ilişkileri esas alan bir denklem ya da denklem sistemi kurularak, ya istenen büyüklüklerin doğrudan doğruya hesaplanması ya da bir ifadenin ispatlanmasıdır. Birleşik yöntemde ise, çözümün bazı adımlarında bir geometrik yöntem, diğer adımlarında ise cebirsel bir yöntem kullanılır.
Hangi çözüm yolu seçilirse seçilsin, bunun başarıyla uygulanması, teoremlerin ve onların kullanımının bilinmesine bağlıdır. Burada düzlem geometrinin bütün teoremlerinden söz etmeyeceğiz.
Geometri problemlerini çözerken sık sık, iki doğru parçasının ya da iki açının birbirine eşit olduğunu kanıtlamamız gerekir. Aşağıda, iki doğru parçasının (uzunlukça) eşit olduğunun kanıtlanmasının üç temel yolu verilmiştir:
$\qquad$ 1. Doğru parçalarını iki üçgenin kenarları olarak kabul eder ve bu üçgenlerin eşit olduklarını ispatlarız.
$\qquad$ 2. Doğru parçalarını bir üçgenin kenarları olarak kabul eder ve bu üçgenin ikizkenar olduğunu ispatlarız.
$\qquad$ 3. Verilen $a$ doğru parçasını kendisine eşit bir $a’$ doğru parçasıyla ve $b$ doğru parçasını kendisine eşit bir $b’$ doğru parçasıyla değiştirir, $a’$ ve $b’$ doğru parçalarının birbirine eşit olduğunu ispatlarız.
Geometri problemlerini çözerken;
$\qquad$ * verilen şekildeki doğruya paralel ya da dik bir doğru çizmek;
$\qquad$ * üçgenin kenarortayını kendisi kadar uzatarak üçgeni paralelkenara çevirmek;
$\qquad$ * yardımcı bir çember çizmek;
$\qquad$ * bir doğrunun çembere teğet olduğu ya da iki çemberin birbirine teğet olduğu noktalardaki yarıçaplarını çizmek;
gibi ek yapılar oluşturmak yoluna da gidebiliriz.
Örnek 1. Birbirine dik iki doğru, $ABCD$ dikdörtgenin $AB$, $BC$, $CD$ ve $AD$ kenarlarını sırasıyla $E$, $F$, $K$ ve $L$ noktalarında kesiyor. $EF=KL$ olduğunu gösteriniz (Şekil 1).
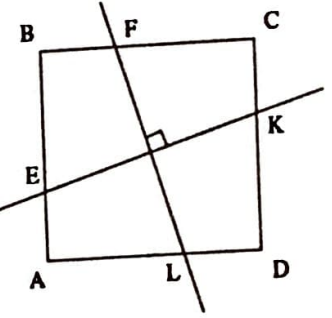
Çözüm. Yukarıda belirtilen yollardan birincisini uygulayarak, $CD$’ye paralel $FM$ ve $AD$’ye paralel $KP$ doğru parçalarını çizelim. Böylece $EK$ ve $FL$ doğru parçaları, $EKP$ ve $FLM$ dik üçgenlerinin kenarları haline gelirler (Şekil 2). Bu iki üçgenin eşit olduğunun kanıtlanması, çözüm için yeterli olacaktır.
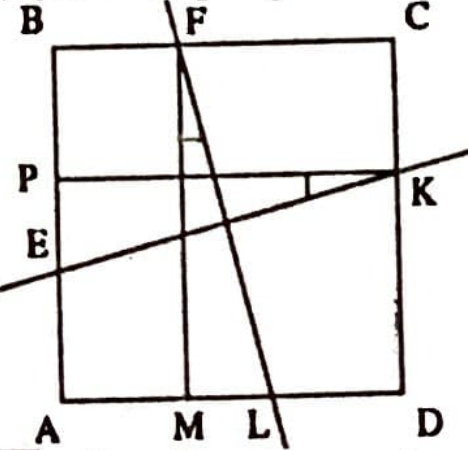
$\overline{PK}=\overline{FM}$ (verilen karenin yükseklikleri), $\sphericalangle{LFM} = \sphericalangle{EKP}$ (kenarları birbirine dik açılır). Bir kenarları ve bir dar açıları eşit olan iki dik üçgen birbirine eşit olduğundan, $\triangle EKP = \triangle FLM$ olacaktır. O halde, bu iki dik üçgenin hipotenüsleri de birbirine eşittir. Yani $\overline{EK} = \overline{FL}$ olmaktadır.
Örnek 2. Kenarları $a$, $b$ ve $c$ olan bir üçgenin $c$ kenarına ait kenarortayının uzunluğunu hesaplayınız.
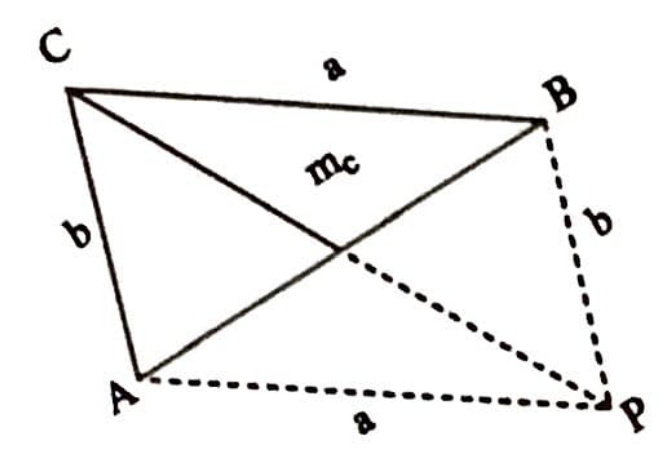
Çözüm. Kenarortayı kendisi kadar uzatıp $ACBP$ paralelkenarını oluşturalım (Şekil 3). Paralelkenarda metrik bağlantıyı uygulayarak $\overline{CP}^2 + \overline{AB}^2 = 2\overline{AC}^2 + 2\overline{BC}^2$ yazabiliriz. Buradan $\left( 2V_c\right)^2 +c^2 = 2b^2+2a^2$ ve $$ V_c=\frac{\sqrt{2a^2+2b^2-c^2}}{2}$$ elde edilir.
Örnek 3. Bir dar açılı üçgenin ortosantrının, yüksekliklerin ayaklarının oluşturduğu üçgenin içteğet çemberinin merkezi ile çakıştığını kanıtlayınız.
Çözüm. Bir üçgenin içteğet çemberinin merkezinin, açıortayların kesim noktası olduğu göz önüne alındığında, problem $DH$, $EH$ ve $KH$’nin, $DEK$ üçgenin açıortayları olduğunun kanıtlanmasına indirgenmiş olur (Şekil 4).
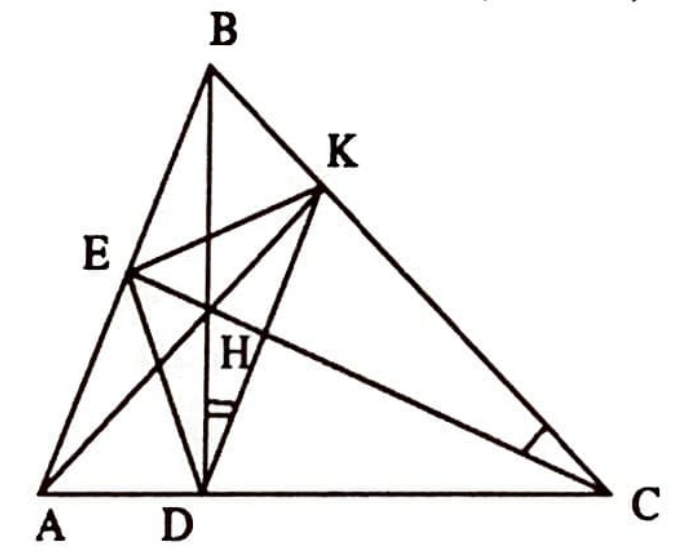
Bunun için de, $\sphericalangle{EDH} = \sphericalangle{HDK}$ olduğunun kanıtlanması yeterli olacaktır.
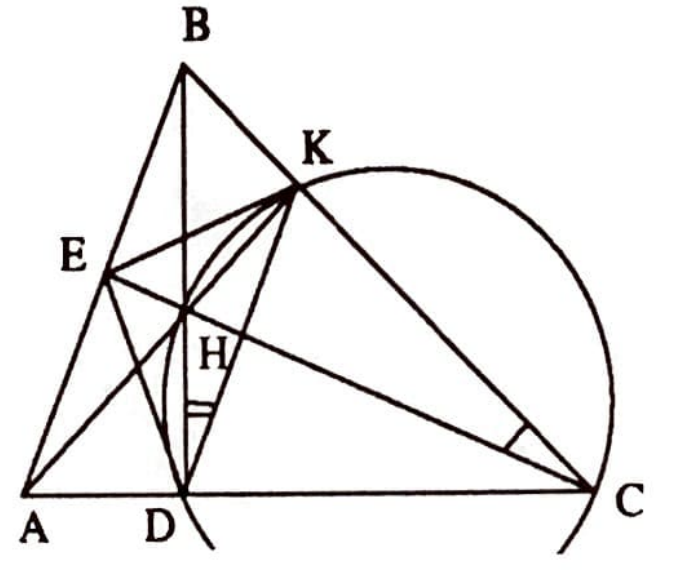
$DHKC$ dörtgeninin göz önüne alalım: $\sphericalangle{HDC} = 90^\circ$ ve $\sphericalangle{HKC} = 90^\circ$. Buradan $\sphericalangle{HDC} + \sphericalangle{HKC}= 180^\circ$ bulunur. O halde $DHKC$ dörtgeninin çevresine bir çember çizilebilir. Bu çemberi çizelim (Şekil 5). $HK$ yayını gören çevre açılar olmaları nedeniyle $\sphericalangle{HDK} =\sphericalangle{HCK}$ bulunur. Öte yandan kenarları birbirine dik açılar olmaları nedeniyle $\sphericalangle{EAH} =\sphericalangle{HCK}$ yazılabilir, ve buradan da $\sphericalangle{EDH}=\sphericalangle{HDK}$ elde edilmiş olur.
Geometri problemlerini cebirsel yöntemle çözerken gerekli denklemleri kurmak için, Pisagor teoremi, dik üçgende metrik ilişkiler, bir dik üçgenin açıları ve kenarları arasındaki ilişkiler, benzer üçgenlerin kenarları, yükseklikleri ve çevrelerinin orantılılığı, açıortay özellikleri, paralelkenar ve çemberdeki metrik ilişkiler, sinüs ve kosinüs teoremleri ile alan hesabı formüllerinden yararlanılır.
Bir referans elemanı yöntemi ise, geometri problemlerini çözerken denklem kurmak için temel bir yöntemdir. Bu yöntem şöyle özetlenebilir. Bir ve aynı eleman (bilinen ve bilinmeyenler cinsinden) iki farklı yolla ifade edilir ve bu ifadeler birbirine eşitlenir. Referans elemanı olarak alan kullanılırsa, problemin alanlar yöntemiyle çözüldüğü söylenir.
Örnek 4. Kenarları $a$, $b$ ve $c$ olan bir üçgenin $h_c$ yüksekliğini hesaplayınız.
Çözüm. Birinci Yöntem. $h_c$ yüksekliği, $ACH$ ve $CHB$ dik üçgenlerinin orta kenarıdır (Şekil 5). ($CH$ kenarını referans elemanı olarak alıp) Pisagor teoremini uygulayarak, $\overline{CH}^2$’yi hem $ACH$ hem de $CHB$ üçgeni için ifade ederiz.
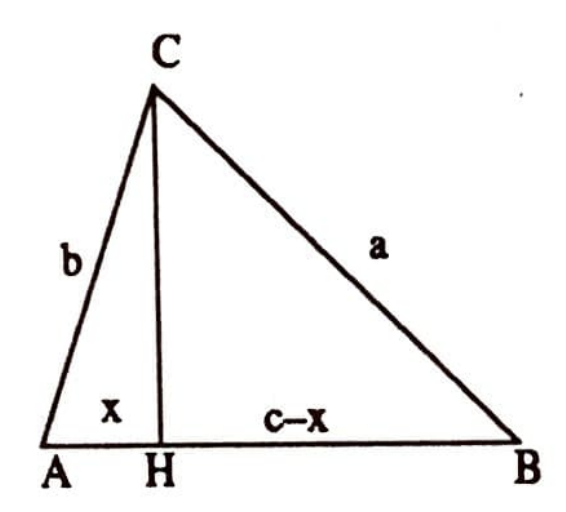
$\overline{AH}=x$ olsun. $\overline{BH}=c-x$ olacaktır. Eğer $ACB$ üçgeni geniş açılı üçgen ise, $\overline{BH} = c+x$ olacaktır (Şekil 6).
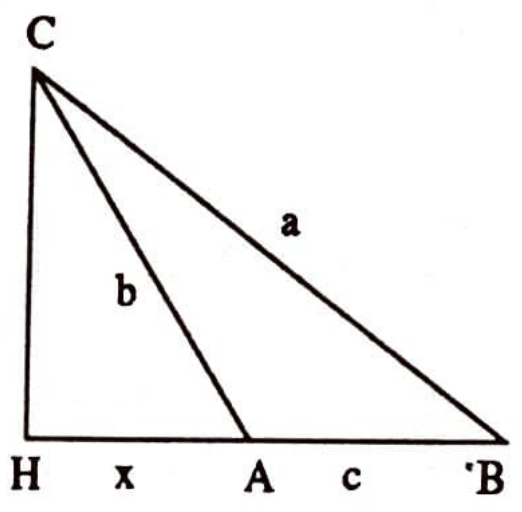
Biz burada yalnızca Şekil 5’teki durumu ele alacağız.
$ACH$ üçgeninden $\overline{CH}^2=b^2-x^2$, $BCH$ üçgeninden ise $\overline{CH}^2=a^2-(c-x)^2$ olarak bulunur. $\overline{CH}^2$ değerlerini birbirine eşitlersek, $b^2-x^2=a^2-(c-x)^2$ bulunur. Buradan $$x = \frac{c^2+b^2-a^2}{2c}$$ elde edilir. $ACH$ üçgeninde Pisagor teoremini uygulayarak aşağıdaki eşitlik bulunur: $$\begin{split}\overline{CH}
&=\sqrt{b^2-\left(\frac{c^2+b^2-a^2}{2c}\right)^2} \\
&= \sqrt{\left(b-\frac{c^2+b^2-a^2}{2c}\right)\left(b+\frac{c^2+b^2-a^2}{2c}\right)} \\ &=\frac{1}{2c}\sqrt{\left( a^2-(b-c)^2\right) \left( (b+c)^2-a^2\right)} \\
&=\frac{1}{2c}\sqrt{(a+b-c)(a-b+c)(-a+b+c)(a+b+c) } \end{split}$$ olarak elde edilir.
İkinci Yöntem. Alanlar yöntemini kullanalım. $ABC$ üçgeninin alanı, bir yandan $S=\sqrt{u(u-a)(u-b)(u-c)}$ formülünden, öte yandan $S=\frac{1}{2}ch_c$ formülünden hesaplanabilir. Bu ifadelerin eşitlenmesi ile $$\frac{1}{2}ch_c = \sqrt{u(u-a)(u-b)(u-c)}$$ elde edilir, ve buradan da $$h_c = \frac{2}{c}\sqrt{u(u-a)(u-b)(u-c)}$$ bulunur. Bu ifadede $u=\frac{a+b+c}{2}$ değerini yerine koyarsak, aşağıdaki sonuca ulaşırız: $$h_c = \frac{\sqrt{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}}{2c} \ .$$
Örnek 5. Bir üçgenin kenarları $a$, $b$ ve $c$ olsun. $C$ açısının açıortayı $n_c$’yi hesaplayınız.
Çözüm. Birinci Yöntem (Cebirsel). $ABC$ üçgeninin $C$ açısının açıortayı $CD$ olsun (Şekil 7).
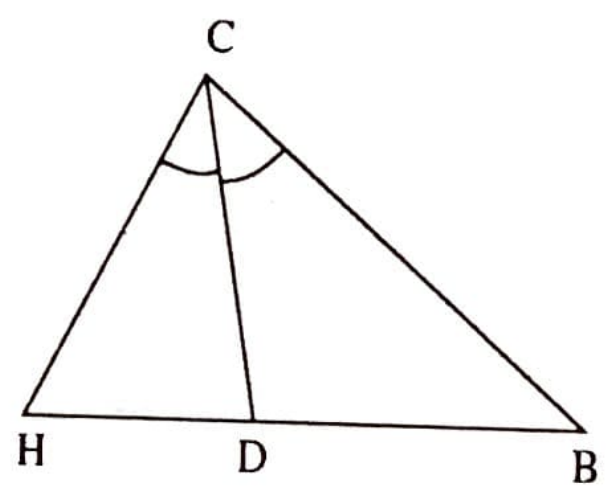
Çözüm yolu şöyle olacaktır.
$AB$ ve $BD$ doğru parçalarının uzunluklarını buluruz. $ACD$ ve $BCD$ üçgenlerine kosinüs teoremini uygulayarak ve $\sphericalangle{ACD} = \sphericalangle{DCB}$ olduğunu göz önüne alarak $CD$’yi buluruz. (Kolaylık olması açısından $\overline{CD}=1$ ve $\sphericalangle{ACD}=\sphericalangle{DCB}=t$ olarak alınmıştır.) $\overline{AD}=x$ ve $\overline{BD}=y$ olsun. O halde $x+y=c$ olacaktır. Öte yandan açıortay özelliğinden; $x/y=a/b$ olduğu bilinmektedir. Bu iki denklemden $x=bc/(a+b)$ ve $y=ac/(a+b)$ olarak elde edilir. $ACD$ üçgenine kosinüs teoremini uygulayarak
$$x^2=b^2+l^2-2bl\cos t ; \tag{1}$$
$BCD$ üçgeninde kosinüs teoremini yazarak
$$y^2=a^2+l^2-2al\cos t \tag{2}$$
bulunur. $(1)$ eşitliğinin iki tarafını $a$ ile ve $(2)$ eşitliğinin iki tarafını $-b$ ile çarpıp taraf tarafa toplarsak $ax^2-by^2=ab^2-a^2b+al^2-bl^2$ elde ederiz. Buradan da
$$l^2=\frac{1}{a-b}(x^2a-y^2b)+ab \tag{3}$$ bulunur. $x$ ve $y$ için yukarıda bulunan ifadeler $(3)$ eşitliğinde yerlerine kolun konulursa,
$$\begin{split} l^2 &= \frac{1}{a-b}\left( \frac{b^2c^2a}{(a+b)^2} -\frac{a^2c^2b}{(a+b)^2} \right) +ab \\
&= ab\left( 1- \frac{c^2}{(a+b)^2}\right)\\
& = \frac{ab(a+b+c)(a+b-c)}{(a+b)^2} \end{split}$$ olarak elde edilir, ve buradan da $$l=\overline{CD}= \frac{\sqrt{ab(a+b+c)(a+b-c)}}{a+b} $$
bulunur.
İkinci Yöntem. Bulmak istediğimiz bilinmeyenin yanına bir yardımcı bilinmeyen ekleyelim ve $x=\sphericalangle{ACD}=\sphericalangle{DCB}$ diyelim, ve alanlar yöntemini kullanan: $S_{ACD}+S_{BCD}=S_{ABC}$. Öte yandan
$$\begin{split} S_{ABC} & = \frac{1}{2}ab\sin 2x \\
S_{ACD} & = \frac{1}{2}bl\sin x\\
S_{BCD} & = \frac{1}{2}al\sin x \end{split}$$ değerlerini göz önüne alarak;
$$\frac{1}{2}ab\sin 2x = \frac{1}{2}bl\sin x+\frac{1}{2}al\sin x$$
eşitliğini elde ederiz. Buradan da
$$ \begin{split} ab\sin x\cos x &=\frac{1}{2}(l(a+b)\sin x) \\
l &= \frac{2 ab\cos x}{a+b}\end{split}$$ buluruz.
$\cos x$’i bulmak için $ABC$ üçgeninde kosinüs teoremini uygulayalım: $c^2=a^2+b^2-2ab\cos 2x$ ve $$\cos 2x = \frac{a^2+b^2-c^2}{2ab}\ .$$
Öte yandan
$$\cos x = \sqrt{\frac{1+\cos 2x}{2}}$$ olduğuna göre, aşağıdaki sonucu elde ederiz:
$$\begin{split} \cos x & = \sqrt{\frac{1}{2}\left(1 + \frac{a^2+b^2-c^2}{2ab} \right)} \\
& = \frac{1}{2}\sqrt{\frac{(a+b+c)(a+b-c)}{ab}} \ . \end{split}$$
Buradan da
$$\begin{split} l & = \frac{2 ab\cos x}{a+b} = \frac{ab}{a+b} \sqrt{\frac{(a+b+c)(a+b-c)}{ab}} \\
&= \frac{\sqrt{ab(a+b+c)(a+b-c)}}{a+b} \end{split}$$ değerini elde ederiz.
Geometri problemlerinin çözümü için denklem kurarken, çözümü kolaylaştırmak için zaman zaman yeni bilmeyenlerin eklenmesi gerekebilir. Bu durumu aşağıdaki örnekle açıklayalım:
Örnek 6. Bir dik üçgende hipotenüs $c$ ve dar açılardan birinin açıortayının ölçüsü $c\frac{\sqrt{3}}{3}$’tür. Dik kenarları bulun (Şekil 8).
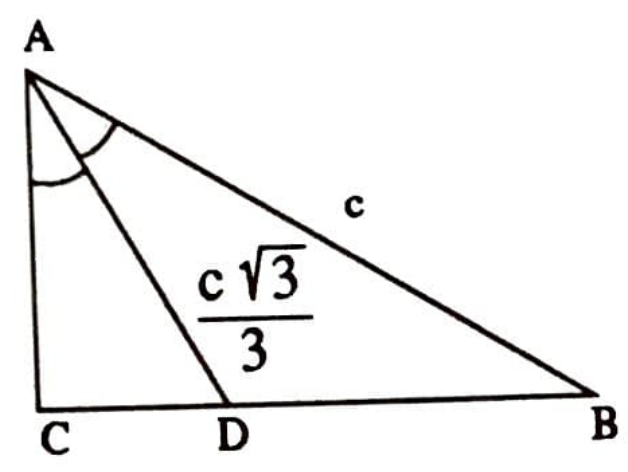
Çözüm. Birinci Yöntem. $\overline{AC}=x$, $\overline{BC}=y$, $\overline{CD}=z$ diyelim. Pisagor teoreminden
$$x^2+y^2=c^2\quad\text{ve}\quad x^2+z^2=\left(\frac{c\sqrt{3}}{3} \right)^2$$
yazabiliriz. Öte yandan, açıortay özelliğinden
$$\frac{\overline{AC}}{\overline{AB}}=\frac{\overline{CD}}{\overline{DB}} \implies \frac{x}{c}=\frac{z}{y-z}$$
yazabiliriz. Sonuçta aşağıdaki üç bilinmeyenli denklem sistemini elde ederiz:
$$\begin{split} x^2+y^2 &=c^2 \\
x^2+z^2&=\frac{c^2}{3} \\
\frac{x}{c}&=\frac{z}{y-z} \end{split}$$
Bu sistemin çözülmesi ise bir hayli zordur.
İkinci Yöntem. $\sphericalangle{CAD}=\sphericalangle{BAD}=x$ diyelim. $AC$ doğru parçasını bir referans elemanı olarak kullanarak bir denklem kuralım. $ABC$ üçgeninden $\overline{AC} = c\cos 2x$; $ACD$ üçgeninden ise $\overline{AC}=\frac{c\sqrt{3}}{3}\cos x$ bulunur. Bu ifadeleri eşitleyerek aşağıdaki trigonometrik denklemi elde ederiz:
$$c\cos 2x = \frac{c\sqrt{3}}{3}\cos x \ .$$
Bu eşitliği çözersek
$$\begin{split} \sqrt{3}\cos 2x &= \cos x \\
\sqrt{3}(2\cos^2 x-1)&=\cos x \\
2\sqrt{3}\cos^2 x – \cos x -\sqrt{3} & = 0 \end{split}$$
buluruz ve buradan da $\cos x = \pm \sqrt{\frac{3}{2}}$ elde ederiz. Problemin verilişine göre $\cos x > 0$ olmalıdır. O halde,
$$\cos x = \sqrt{\frac{3}{2}} \implies \sphericalangle{BAD}=30^\circ,\, \sphericalangle{BAC}=60^\circ$$
olacaktır. Bunları kullanarak
$$\overline{AC}=\frac{c}{2}\quad \text{ve}\quad \overline{BC}=\frac{c\sqrt{3}}{2} $$
sonucunu buluruz.
Eğer bir problemde (uzunluklar ya da alanlar gibi) bazı büyüklüklerin oranının bulunması gerekiyorsa ya da özel olarak bir açının hesaplanması gerekiyorsa (bu durum, o açının bir fonksiyonunun bulunmasına ve dolayısıyla da bir dik üçgenin kenarlarının oranının hesaplanmasına indirgenebilir), genellikle aşağıdaki yolu izleriz:
Doğrusal elemanlardan birini bilinen kabul eder, hesaplanması istenen büyüklükleri bu eleman cinsinden ifade eder ve sonra da bunların oranını oluştururuz. Bu doğrusal elemana yardımcı parametre denir ve bu çözüm yolu yardımcı parametre kullanılması yöntemi olarak adlandırılır. Geometrik şekillerin benzerliğinin söz konusu olduğu problemlerin çözümünde kullanılır.
Örnek 7. Bir $ABC$ dik üçgeninin hipotenüsüne ait kenarortayı ile yüksekliği arasındaki açının değeri $\arccos (40/41)$’dir. Dik kenarlarının oranını bulunuz (Şekil 9).
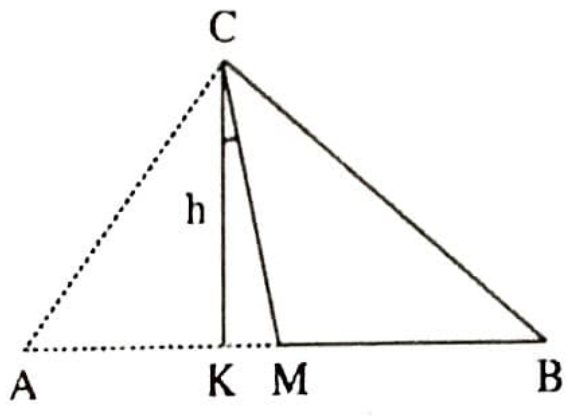
Çözüm. Önce verilenlerden $\cos \alpha = \frac{40}{41}$, yani $\frac{\overline{CK}}{\overline{CM}}=\frac{40}{41}$ olduğu sonucunun çıkarılabileceğini dikkat edelim. Problemi yardımcı parametre yöntemiyle çözeceğiz.
$\overline{CK}=h$ diyelim. Buna göre $\overline{CM}=\frac{41}{40}h$ ve $$ \overline{KM} =\sqrt{\overline{CM}^2-\overline{CK}^2} = \frac{9}{40}h$$ olacaktır. Bir dik üçgende kenarortayın hipotenüsün yarısına işte olduğunu biliyoruz. O halde $$\overline{AM}=\overline{CM}=\overline{MB}=\frac{41}{40}h$$ olacaktır. Buradan da,
$$\begin{split} \overline{AK} &= \overline{AM}-\overline{KM}=\frac{41}{40}h-\frac{9}{40}h=\frac{4}{5}h \\
\overline{KB} &= \overline{KM}+\overline{BM}= \frac{9}{40}h+\frac{41}{40}h=\frac{5}{4}h\\
\overline{AC} &= \sqrt{\overline{AK}^2+\overline{CK}^2}=\sqrt{\frac{16}{25}h^2+h^2} =\frac{h}{5}\sqrt{41} \\
\overline{BC} &= \sqrt{\overline{BK}^2 +\overline{CK}^2} = \sqrt{\frac{25}{16}h^2+h^2}=\frac{h}{4}\sqrt{41}
\end{split}$$ bulunur.
Örnek 8. Bir ikizkenar $ABC$ üçgenin tepe açısı $C$, $100^\circ$’dir. Başlangıcı $A$ olan ve ${AB}$ ile $30^\circ$’lik açı yapan bir ışın ile başlangıcı $B$ olan ve $AB$ ile $20^\circ$’lik açı yapan ikinci bir ışın çiziliyor. Bu ışınlar $M$ noktasında kesişiyorlar. $\sphericalangle{ACM}$ ve $\sphericalangle{BCM}$ açılarını bulunuz.
Çözüm. $M$ ve $C$ noktalarını birleştirelim ve $ACM$ açısına $x$ diyelim. Sonra $M$ noktasından üçgenin kenarlarına dikler çizelim:
$$ \overline{MC_1} \perp \overline{AB},\quad \overline{MB_1} \perp \overline{AC},\quad \overline{MA_1} \perp \overline{BC} \ . $$ $\overline{MC}=a$ diyerek yardımcı bir parametre kullanır ve $\overline{MC_1}$’i referans elemanı olarak alıp $\overline{MC_1}$’i iki yolla hesaplarız.
$CMB_1$ üçgeninden $\overline{MB_1}=\overline{MC}\sin x = a \sin x$ buluruz. $\sphericalangle{ACB}=100^\circ$ ve üçgen ikizkenar olduğu için, $\sphericalangle{CAB}=\sphericalangle{ABC}=40^\circ$ ve $\sphericalangle{CAM}=10^\circ$ olacaktır. $AMB_1$ üçgeninden $$ \overline{AM}=\frac{\overline{MB_1}}{\sin 10^\circ} = \frac{a\sin x}{\sin 10^\circ},$$
$AMC_1$ üçgeninden ise $$\overline{MC_1}= \overline{AM}\sin 30^\circ = \frac{a\sin x}{2\sin 10^\circ} $$
bulunur.
$CMA_1$ üçgenini göz önüne alalım: $\sphericalangle{MCA_1}=100^\circ-x$. Dolayısıyla
$$\overline{MA_1}= \overline{CM}\sin (100^\circ-x)=a\sin (100^\circ-x), $$
ve $BMC_1$ ile $BMA_1$ üçgenleri eş olduğu için
$$\overline{MC_1}= \overline{MA_1}=a\sin (100^\circ-x). $$
$\overline{MC_1}$ için bulunan ifadeleri eşitleyerek aşağıdaki trigonometrik denklemi elde ederiz:
$$\frac{a\sin x}{2\sin 10^\circ} = a\sin(100^\circ -x).$$
Bu denklemi çözerek sonuca ulaşırız:
$$\begin{split} & \sin x = 2\sin(100^\circ -x)\sin 10^\circ = \cos(90^\circ -x )-\cos(110^\circ-x) \\
\implies &\cos(110^\circ-x) =0 \\
\implies & x = 20^\circ\ .\end{split}$$
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

