Yazar: Emre Alkan (Boğaziçi Üniversitesi Matematik Bölümü öğrencisi)
Yıl: 1994-4
Bu yazıda okuyucuya bir dizi ilginç problem sunmaya çalışacağız. P. Erdös’e ait iki güzel problemle başlayalım.
Problem 1. Geniş açılı olmayan, çevrel ve iç yarıçapları $R$ ve $r$, yükseklikleri $h_a$, $h_b$, $h_c$ olan bir $ABC$ üçgeninde $R+r \leq \max \{ h_a, h_b, h_c \}$olduğunu gösteriniz.
Çözüm. $ABC$ üçgeninin ortosantrını (yüksekliklerinin kesim noktasını) ve çevrel çember merkezini $H$ ve $O$ ile gösterelim. Şu teoremleri göz önüne alalım.
$\hphantom{ii}(\text{i})\;$ $O$’nun $ABC$’nin kenarlarına uzaklıklarının toplamı $R+r$’dir.
$\hphantom{i}(\text{ii})\;$ $O$’dan kenarlara inilen dikme ayakları $A’$, $B’$, $C’$ olsun. Bu durumda $HA=2\cdot OA’$, $HB=2\cdot OB’$, $HC=2\cdot OC’$ eşitlikleri geçerlidir.
$(\text{iii})\;$ $H$’nin kenarlara göre simetrikleri çevrel çember üzerindedir.
Bu teoremlerin ispatlarını okuyucuya bırakacağız.
Üçgenin açıları için $A\leq B \leq C$ alalım. Böylece $ \max \{ h_a, h_b, h_c \}=h_a$ olur. Ortosantrın $BC$ kenarına göre simetriği $H’$ olsun. $(\text{i})$, $(\text{ii})$ ve $(\text{iii})$ kullanılarak $R+r \leq h_a$ eşitsizliğinin $BH’+CH’ \leq AH’$ eşitsizliğine dönüştüğü gözlenebilir. Sinüs teoremi yardımıyla bu eşitsizliğin $\cos B +\cos C \leq AH’$ eşitsizliğine dönüştüğü gözlenebilir. Kosinüs teoremi yardımıyla bu eşitsizlik $$\cos B +\cos C \leq \cos(B-C)=\cos B \cos C +\sin B\sin C$$ eşitsizliğine dönüşür. $\cos B =x$ ve $\cos C=y$ alalım. Böylece $x+y\leq xy+\sqrt{1-x^2}\sqrt{1-y^2}$. Üçgen geniş açılı olmadığından $x\geq 0$, $y\geq 0$ kısıtlamaları var. Ayrıca $2B \geq \pi -C$ ve $2C\geq \pi -B$ olduğundan, $\cos B\leq \sin\frac{C}{2}$ ve $\cos C \leq \sin\frac{B}{2}$, yani $2x^2+y\leq 1$ ve $x+2y^2\leq 1$ kısıtlamaları da elde edilir.
Şimdi $$f(x,y)=xy+\sqrt{1-x^2}\sqrt{1-y^2}-x-y$$
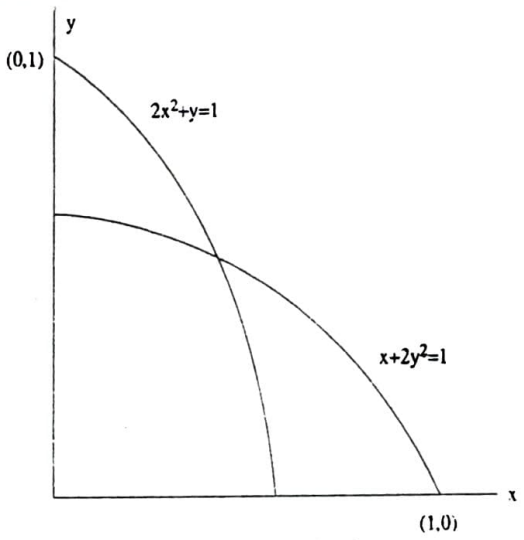
fonksiyonunun $x=0$, $y=0$, $2x^2+y = 1$ ve $x+ 2y^2 = 1$ ile belirli olan bölgede minimum değerini arayalım.
$$\begin{split} \frac{\partial f}{\partial x} &= y-\frac{x}{\sqrt{1-x^2}}\sqrt{1-y^2} -1 =0 \\
\frac{\partial f}{\partial y} &= x-\frac{y}{\sqrt{1-y^2}}\sqrt{1-x^2} -1 =0 \end{split}$$ şartlarından $$\begin{split} \sqrt{1-y} \left( \sqrt{1-y} \sqrt{1-x^2} + x \sqrt{1+y}\right) &=0 \\
\sqrt{1-x} \left( \sqrt{1-x} \sqrt{1-y^2} + y\sqrt{1+x}\right) &=0 \end{split}$$elde edilir. $\sqrt{1-y}\sqrt{1-x^2}+x\sqrt{1+y}=0$ veya $y=1$ olmalıdır. $y=1$ ise, bu ikinci eşitlikte kullanılarak $x=1$ veya $x=-1$ elde edilir. $x\geq 0$ olduğundan $(1,1)$ çifti geçerlidir. Fakat bu nokta bölgeye dahil değildir. Diğer olasılıklar da incelenirse tek mümkün çözümün $(1,1)$ olduğu anlaşılır. Şu halde minimumu bölgenin sınırlarında aramalıyız.
$x=0$ olsun. $f(0,y)=\sqrt{1-y^2}-y$ ve $0\leq y \leq 1$ için $\frac{\partial f}{\partial y} = -\frac{y}{\sqrt{1-y^2}}-1 =0$ olduğundan çözüm yok. $y=0$ olunca da minimum adayı yok.
$2x^2+y = 1$ olsun. $f(x,y)=-4x^3+2x^2+2x-1$ ve $x\geq 0$ için $-6x^3+2x+1=0$ olduğundan $x=\frac{1+\sqrt{7}}{6} \cong 0.6$ elde edilir. Bu bir minimum adayıdır. Bu durumda $f(x,y)\cong 0.06$ bulunur. $x+ 2y^2 = 1$ olunca da aynı duruma varılacaktır.
Son olarak da kritik noktalara bakalım. $f(0,0)=1$, $f\big( \frac{\sqrt{2}}{2} , 0 \big)=0$ , $f\big( 0, \frac{\sqrt{2}}{2} \big)=0$, ve parabollerin kesim noktasında $f\big( \frac{1}{2} , \frac{1}{2} \big)=0$. Şu halde bu bölgede $f(x,y)\geq 0$ olduğunu gözlemiş olduk.
$R+r \leq \max \{ h_a, h_b, h_c \}$’de eşitlik hali $ABC$ eşkenarken veya ikizkenar dik üçgenken sağlanacaktır. $\square$
Problem 2. Köşeleri birim çember üzerinde olan bir $ABC$ üçgeninin içinde alınan bir $P$ noktası için $PA\cdot PB \cdot PC <\frac{32}{27}$ olduğunu ve $\frac{32}{27}$’nin en iyi üst sınır olduğunu gösteriniz.
Çözüm. Birim çemberin içinde bir $P$ noktası alalım ve $P$’yi merkez $O$ ile birleştirerek $B’C’$ çapını oluşturalım. Rastgele bir $ABC$ üçgeni aldığımız zaman $P$, $ABC$’nin içinde olduğundan $A$, $B$ köşeleri çapın bir tarafına, $C$ köşesi de çapın öteki tarafına düşecektir. Aynı nedenden dolayı $C$ köşesi küçük $A’C’$ yayı üzerinde olamaz.
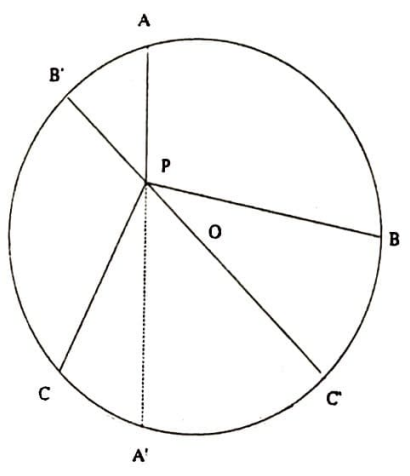
Kolayca $PC<PA’$ ve $PB < PC’$ olduğu görülebilir. $PB’=x$ alınarak, $$PA\cdot PB \cdot PC <PA\cdot PA’ \cdot PC’ =x(2-x)^2 $$ elde edilir. $f(x)=x(2-x)^2 $’nin maksimumu $x=\frac{2}{3}$’te sağlanır ve $PA\cdot PB \cdot PC < f(\frac{2}{3})=\frac{32}{27}$ elde edilir. $\frac{32}{27}$’nin en iyi üst sınır olduğu aşağıdaki şekilden görülmektedir. $\square$
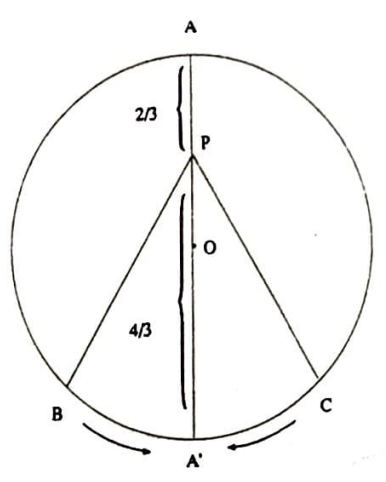
Problem 3. Bir $ABC$ üçgeninde içmerkez $I$ olsun. $AI$, $BI$, $CI$ doğruları çevrel çemberi sırayla $A’$, $B’$ ve $C’$’de kessin. $2(AI+BI+CI) \leq AA’+BB’+CC’$ olduğunu gösteriniz.
Çözüm. İspatını okuyucuya bırakacağımız şu teoreme bakalım.
$AI$, $BI$, $CI$ doğruları, $A’$, $B’$, $C’$ noktalarını köşe kabul eden üçgenin yükseklikleridir.
$B’C’$, $AA’$’yü $A^{\prime\prime}$’de kessin. $B^{\prime\prime}$ ve $C^{\prime\prime}$ de benzer şekilde tanımlansın. Erdös-Mordell eşitsizliğine göre $$2(IA^{\prime\prime}+IB^{\prime\prime}+IC^{\prime\prime}) \leq IA’+IB’+IC’\ .$$
$2\cdot IA^{\prime\prime}=AI$, $2\cdot IB^{\prime\prime}=BI$, $2\cdot IC^{\prime\prime}=CI$ olduğunu kullanarak, $AI+BI+CI\leq IA’+IB’+IC’$ ve istenen $2(AI+BI+CI)\leq A’A+B’B+C’C$’yi elde ederiz. $\square$
Problem 4. $a$, $b$, $c$ bir üçgenin kenarları, $p$, $q$, $r$ ise pozitif sayılar olsun. $S$ üçgenin alanı olmak üzere, $$ \frac{p}{q+r}a^2 +\frac{q}{p+r}b^2 + \frac{r}{p+q}c^2 \geq 2\sqrt{3}S$$ olduğunu gösteriniz.
Çözüm. $q+r=x$, $p+r=y$, $p+q=z$ alalım; $x$, $y$, $z$ pozitiftir.
$$\frac{-x+y+z}{x}a^2 + \frac{x-y+z}{y}b^2 + \frac{x+y-z}{z}c^2 \geq 4\sqrt{3}S$$ olduğunu görmeliyiz. Böylece $$\left(\frac{y}{x}a^2 + \frac{x}{y}b^2\right)+ \left(\frac{z}{x}a^2 + \frac{x}{z}c^2\right)+\left(\frac{z}{y}b^2 + \frac{y}{z}c^2\right) \,-\, (a^2+b^2+c^2) \geq 4\sqrt{3}S\ .$$
$\frac{y}{x}a^2 + \frac{x}{y}b^2 \geq 2ab$, ve diğerleri için de yapılırsa, $$ 2(ab+ac+bc)- (a^2+b^2+c^2) \geq 4\sqrt{3}S$$ olduğunu görmek yeterlidir.
$$ab+ac+bc = 2S\left(\frac{1}{\sin A} + \frac{1}{\sin B} +\frac{1}{\sin C}\right)$$ ve $$a^2+b^2+c^2 = 4S(\cot A+\cot B+\cot C)$$ olduğu göz önüne alınırsa, $$ \frac{1}{\sin A} + \frac{1}{\sin B} +\frac{1}{\sin C}-(\cot A+\cot B+\cot C)\geq \sqrt{3}$$ ve $$\frac{1}{\sin \alpha} -\cot \alpha = \tan\frac{\alpha}{2}$$ olduğundan, $$ \tan\frac{A}{2}+\tan\frac{B}{2}+\tan\frac{C}{2}\geq \sqrt{3}$$elde edilir. Bu son eşitsizliği okuyucuya bırakacağız. $\square$
Problem 5. Kenarları $a_i$, $b_i$, $c_i$, $i=1,2,\ldots,n$, olan $n$ tane üçgen göz önüne alınız. Yarıçevreleri $v_i$, çevrel ve içteğet çember yarıçapıları $R_i$ ve $r_i$ olmak üzere, $$3 \left[\prod_{i=1}^na_i^{-\frac{1}{n}}+\prod_{i=1}^nb_i^{-\frac{1}{n}}+\prod_{i=1}^nc_i^{-\frac{1}{n}} \right] \leq \prod_{i=1}^n\left( \frac{v_i}{R_ir_i}\right)^{\frac{1}{n}}$$ olduğunu gösteriniz.
Çözüm. $p_i$, $i=1,2,\ldots,n$, çevreleri göstersin. $\frac{v_i}{R_ir_i}=\frac{p_i^2}{a_ib_ic_i}$ olduğu kullanıldığında eşitsizlik $$ 3 \left[\prod_{i=1}^na_i^{\frac{1}{n}}\prod_{i=1}^nb_i^{\frac{1}{n}}+\prod_{i=1}^na_i^{\frac{1}{n}}\prod_{i=1}^nc_i^{\frac{1}{n}}+\prod_{i=1}^nb_i^{\frac{1}{n}}\prod_{i=1}^nc_i^{\frac{1}{n}} \right] \leq \prod_{i=1}^np_i^{\frac{2}{n}} $$ halini alır. $p_i$’leri sabit tutalım. Böylece sağ taraf sabit kalacaktır. Sol taraf $$ 3 \left[\prod_{i=1}^na_i^{\frac{1}{n}} \left( \prod_{i=1}^nb_i^{\frac{1}{n}}+\prod_{i=1}^nc_i^{\frac{1}{n}} \right)+\prod_{i=1}^nb_i^{\frac{1}{n}}\prod_{i=1}^nc_i^{\frac{1}{n}} \right]$$ şeklinde yazılabilir. $$\prod_{i=1}^nb_i^{\frac{1}{n}}\prod_{i=1}^nc_i^{\frac{1}{n}} = \prod_{i=1}^n(b_ic_i)^{\frac{1}{n}}$$ ifadesi $b_i=c_i$ olduğunda maksimumdur. Öte yandan $$ \prod_{i=1}^nb_i^{\frac{1}{n}}+\prod_{i=1}^nc_i^{\frac{1}{n}}\leq \frac{1}{n}\sum_{i=1}^n (b_i+c_i)=\text{Sabit.}$$
Eşitlik yine $b_i=c_i$ iken vardır. $a_i,b_i$ ve $c_i$ simetrik olduğundan sol taraf $a_i=b_i=c_i$ olduğunda maksimum olur. Bu durum eşitlik halidir. $\square$
Problem 6. Bir üçgenin içinde alınan bir noktanın köşelere uzaklıkları $R_1$, $R_2$, $R_3$, kenarlara uzaklıkları ise $\Gamma_1$, $\Gamma_2$, $\Gamma_3$ olsun. $R_1R_2R_3 \geq 8\Gamma_1\Gamma_2\Gamma_3$ olduğunu gösteriniz.
Çözüm. Şekilden $R_1/R_2=\sin\theta_2/\sin\theta_1$ görülüyor. Diğerleri de yazılıp çarpılırsa $k=\sin\theta_1\sin\theta_3\sin\theta_5=\sin\theta_2\sin\theta_4\sin\theta_6$ yazılabilir.
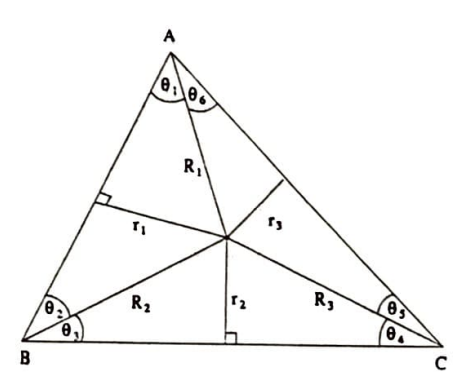
Öte yandan $$\begin{split} \sin\theta_1\sin\theta_6 &\leq \sin^2\frac{A}{2}\\
\sin\theta_2\sin\theta_3 &\leq \sin^2\frac{B}{2}\\
\sin\theta_4\sin\theta_5 &\leq \sin^2\frac{C}{2} \end{split}$$ eşitsizlikleri gösterilebilir. Bunlar çarpılıp, $$ \sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}=\frac{\Gamma}{4R}\leq \frac{1}{8}$$olduğu kullanılarak, $k^2\leq \frac{1}{64}$, $k\leq \frac{1}{8}$ ve $$k = \frac{\Gamma_1\Gamma_2\Gamma_3}{R_1R_2R_3}$$ olduğundan istenen elde edilir. $\square$
Problem 7. $F$ ve $F^\prime$ bir çemberin içinde merkeze göre simetrik iki nokta olsun. $S$ ise çember üzerinde, fakat $FF^\prime$ doğrusu üzerinde olmayan bir nokta olsun. $SF’$ ve $SF$ doğruları çemberi $P’$ ve $P$’de kessin. $P’$ ve $P$’deki teğetler $T$’de kesişsin. $FF^\prime$ doğru parçasının orta dikmesinin $ST$’nin orta noktasından geçtiğini gösteriniz.
Çözüm. Şekilde $SF=x$, $FP=u$, $SF’=y$, $F’P’=v$, ayrıca $x+u=c$, $y+v=b$, $PP’=a$, açılar için $\alpha+\beta=A$, $\sphericalangle{SPP’}=B$, $\sphericalangle{SP’P}=C$ alınmıştır. $M$, $ST$’nin ortasıdır. İsteneni göstermek için $\overline{FM}=\overline{F’M}$ olduğunu göstereceğiz.
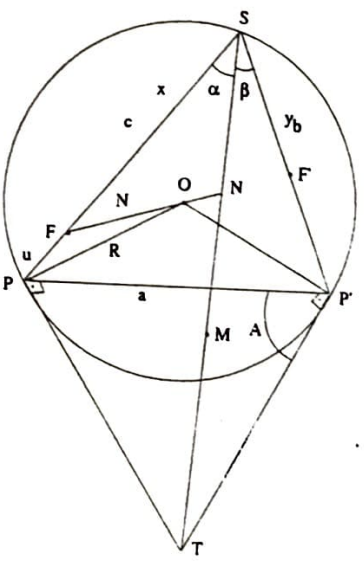
$$\begin{split} \overline{FM}^2 &= x^2+ \overline{MS}^2 -2x\overline{MS}\cos\alpha,\\
\overline{F’M}^2 &= y^2+ \overline{MS}^2 -2y\overline{MS}\cos\beta; \end{split}$$ şu halde aşağıda $$ x^2-y^2=2x\overline{MS}\cos\alpha -2y\overline{MS}\cos\beta$$ olduğunu görmeliyiz.
Çemberde kuvvetten $x(c-x)=y(b-y)$ olduğundan $cx-by=x^2-y^2$ olur. Böylece istenen $$\begin{split}cx-by&=2x\overline{MS}\cos\alpha -2y\overline{MS}\cos\beta\\
\implies\; \frac{x}{y}&= \frac{2\overline{MS}\cos\beta-b}{2\overline{MS}\cos\alpha-c} \\
\implies\; \frac{x}{y}&= \frac{v}{u}\end{split}$$dur. Ayrıca $\frac{v}{u}=\frac{\cos B}{\cos C}$ olduğu kolayca görülebilir. Şu halde istenen $$\frac{\cos B}{\cos C} = \frac{2\overline{MS}\cos\beta-b}{2\overline{MS}\cos\alpha-c}\ .$$
Öte yandan, $$2\overline{MS}\cos\beta=\frac{\overline{ST}^2+b^2-\frac{a^2}{4\cos^2A}}{2b}$$ ve $2\overline{MS}\cos\alpha$ da benzer şekilde yazılırsa istenen $$ \frac{\overline{ST}^2-b^2-\frac{a^2}{4\cos^2A}}{\overline{ST}^2-c^2-\frac{a^2}{4\cos^2A}}\frac{c}{b}=\frac{\cos B}{\cos C}$$ olur. Son olarak, $$\begin{split}\overline{ST}^2&=b^2+\frac{a^2}{4\cos^2A}+ab\frac{\cos B}{\cos A} \\
&=c^2+\frac{a^2}{4\cos^2A}+ac\frac{\cos C}{\cos A} \end{split}$$ olduğu kullanılırsa, $$\frac{\frac{ab\cos B}{\cos A}}{\frac{ac\cos C}{\cos A}}\frac{c}{b}=\frac{\cos B}{\cos C}$$ elde edilir. Dolayısıyla $\overline{FM}^2=\overline{F’M}^2$ ve $\overline{FM}=\overline{F’M}$’dir. $\square$
Not. Bu problem Hüseyin Demir ve Cem Tezer tarafından American Mathematical Monthly’de 1991 yılında Problem E3422 olarak yayımlandı. Problemin aslında $F’$ ve $F$’nin çemberin içinde olması gerekmiyor. $F’$ ve $F$ çemberin dışındayken de benzer bir ispat yapılabileceğini umuyorum. Fakat şu an bunu başaramadığım için probleme içinde olma koşuluna ekledim. $F’$ ve $F$ dışarıdayken çizim farklı olduğundan her şeyi yeniden düzenlemek gerekiyor.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 4. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

