Yazar: Ali Nesin
Yıl: 1994-4
Bu yazıyla başlayan yazı dizimizde oyunları konu edeceğiz. Yazılarımız birbirinden bağımsız olacaklar. Birini anlamak için bir öncesini illa okumuş olmak gerekmez.
Oyunları sonlu ve sonsuz oyunlar diye ikiye ayıracağız. Sonsuz oyunları da ikiye ayıracağız: uygulamada sonsuza dek sürebilen ve süremeyen oyunlar. Şimdilik sonlu oyunları konu edeceğiz.
Satranç sonlu bir oyundur. Ancak satrancın sonlu olması için özel kurallar konmuştur. Örneğin, “bilmem kaç hamlede piyonlara dokunulmazsa oyun berabere biter” diye bir kural vardır. Bu kural olmasaydı, yalnızca iki şahın kaldığı oyunlar sonsuza değin sürerdi. Pişti, briç gibi oyunlar da sonludur. Genellikle kağıt oyunları sonludur. Bu oyunların sonlu olduğunu kanıtlamak oldukça kolaydır, kullanılacak kağıt sayısı sonludur ve gittikçe azalır.
Bazı oyunların bitip bitmeyeceğini önceden kestirmek kolay değildir. Hatta önsezinin bile yetersiz kaldığı olabilir. Önsezi kazanmak ve teoremin doğruluna kendilerini inandırmak için matematikçiler sık sık deneye başvururlar. Bu yöntemi bir oyun için kullanacağız.
Yazı – Tura Üzerine
İki kişi arasında oynanan şu oyunu ele alalım: Oyuncular yazı-tura atıyorlar. Yazı gelirse birinci oyuncu, tura gelirse ikinci oyuncu kazanacak. Birinci oyuncu oyunun başında ortaya 1 lira koyuyor. Kaybettikçe ortaya koyduğu parayı iki misli arttırıyor. Örneğin, ilk atışta kaybederse ortaya 2 lira koyuyor. Bu atışta da kaybederse, üçüncü atışta ortaya 4 lira koyuyor. Gene kaybederse 8 lira koyacak. Kazanınca arttırmayı durduruyor ve hemen sonraki atışta ortaya 1 lira koyuyor. Oyun böyle sürüyor. İkinci oyuncu para alıp vermekle yetiniyor. Eğer iki oyuncudan birinde para kalmazsa ya da birinci oyuncu açıkladığımız stratejisini sürdüremezse oyun bitiyor. Bu oyun bitmemezlik eder mi?
Diyelim, oyunun başında her iki oyuncunun da dörder lirası var. Oyunun başında birinci oyuncu 1 lira ortaya sürüyor. Bu duruma $(4, 4, 1)$ durumu diyelim. Buradaki birinci sayı, birinci oyuncunun cebindeki para; ikinci sayı ikinci oyuncunun cebindeki para; üçüncü sayıysa ortaya sürülen para. Bu durumda tura gelirse, yani birinci oyuncu kaybederse, $(3, 5, 2)$ durumuna geçeceğiz; çünkü birinci oyuncunun 3 lirası kalacak, ikinci oyuncunun 5 lirası olacak ve ortaya sürülen para 2 lira olacak. Bir kez daha tura gelirse, $(1, 7, 4)$ durumuna ulaşırız ve bu durumda oyun biter; çünkü bu durumda birinci oyuncu 4 lira ortaya koymalıdır, ancak 4 lirası yoktur.
Bu oyunun bittiğini nasıl gösterebiliriz? Oyunun bir şemasını çıkarabiliriz. En tepeye $(4, 4, 1)$ yazalım. Bu oyunun birinci durumu. Bu durumdan aşağı doğru sağlı sollu iki ok çıkaralım: tura oku ve yazı oku. Soldaki ok tura geldiğini, yani birinci oyuncunun kaybettiğini, sağdaki oksa kazandığını gösteriyor. Sol okun ucuna birinci oyuncu kaybettiğinde varacağımız durumu yazalım: $(3, 5, 2)$. Sağ okun ucunaysa birinci oyuncu kazandığında varılacak durumu yazalım: $(5, 3, 1)$. Birinci oyuncunun stratejisini sürdüremediği durumlarda oyun bitmiştir. Oyun şeması aşağıda görülüyor.
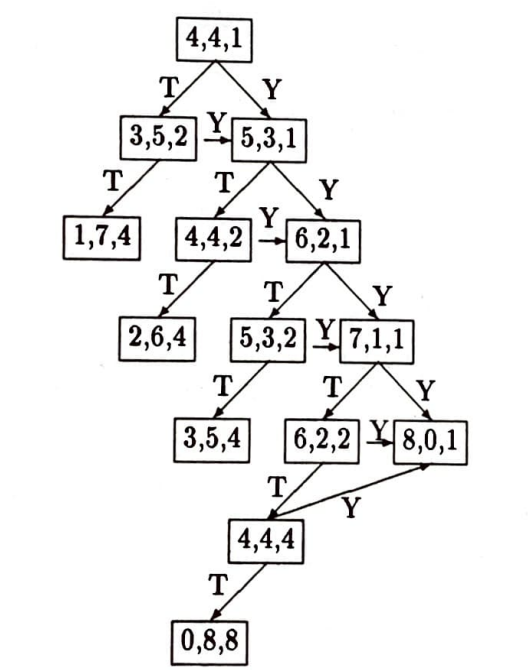
Bu, sonlu bir oyunun şemasıdır, çünkü okları izleyerek bir döngü elde edemeyiz. okların gösterdiği yolları izlediğimizde son durumlardan birine erişiriz.
Oyuna her iki oyuncu da dörder lirayla başladığında oyunun sonlu olduğunu gördük. Okur oyunu başka durumlardan da başlatabilir. Her seferinde oyunun sonlu olduğunu görecektir. “Demek ki,” diye düşünür matematikçi bu aşamada, “bu oyun bitmeli!” Arkasından soruyu genel olarak yanıtlar.
Teorem. Oyuncular oyuna kaç parayla başlarlarsa başlasınlar yukarıdaki oyun biter.
Kanıt. Birinci oyuncu hep kaybederse oyun elbette biter. Birinci oyuncunun peşpeşe $n$ kez kaybettiğini ama bir sonraki $(n+1)$’inci atışta kazandığını varsayalım. İlk $n$ atışta birinci oyuncu $$1 + 2 + 2^2 + … + 2^{n-2} + 2^{n-1}$$ lira kaybetmiş olacaktır. Bu sayıya $S_n$ diyelim: $$(1) \quad \quad S_n = 1 + 2 + 2^2 + … + 2^{n-2} + 2^{n-1}.$$
$S_n$ sayısını hesaplayalım. $(1)$ eşitliğinin sağındaki ve solundaki terimleri $2$’yle çarpacak olursak, $$(2) \quad \quad 2S_n= 2 + 2^2 + 2^3 + … + 2^{n-1} + 2^{n}$$ eşitliğini buluruz. $(1)$ eşitliğini $(2)$’den çıkaralım. Sol tarafta $2S_n – S_n$, yani $S_n$ buluruz. Sağ taraftaysa hemen hemen bütün terimler sadeleşir ve geriye $2^n-1$ kalır. Dolayısıyla $$S_n = 2^n -1$$dir. Demek ki, bir oyuncu peşpeşe $n$ kez kaybederse, $2^n-1$ lira kaybedecektir. Ama bir sonraki atışla, yani $(n+1)$’inci atışla kazandığında $2^n$ (toplam kaybettiklerinin bir fazlasını) kazanacaktır. Dolayısıyla, birinci oyuncu her kazanışında daha önce kaybettiklerini çıkardığı gibi, 1 lira da kazançlı çıkacaktır. Bu ne demektir? Birinci oyuncu kaybetmedikçe 1 lira kazanmayı sürdürecek ve bir zaman sonra da ikinci oyuncunun bütün parasını ütecek demektir. Teoremimiz kanıtlanmıştır.$^1$
Beklenti. Bir oyunun beklentisi, oyuncunun ortalama ne kadar kazanacağını ya da kaybedeceğini gösteren bir sayıdır. Bir örnekle beklentinin nasıl hesaplandığını açıklayayım. Diyelim bir piyango bileti aldınız. Piyango bileti 10 lira. Toplam 100 biletin olduğunu varsayalım. Diyelim 1 bilete 500 lira çıkacak, 2 bilete 100 lira çıkacak ve 5 bilete de 10 lira (yani amorti) çıkacak. Aynı bilete iki ya da daha fazla ikramiye çıkmasına kuralların olanak vermediğini varsayalım. Piyango biletinden beklentiniz nedir? Yüzde 1 olasılıkla 490 lira kazanacaksınız (490 = 500 – 10); yüzde 2 olasılıkla 90 lira lira kazanacaksınız; yüzde 5 olasılıkla amorti çıkacak, yani ne kazanacak ne de kaybedeceksiniz; geri kalan yüzde 92 olasılıkla aldığınız bilete hiçbir şey çıkmayacak ve bilete verdiğiniz 10 lira yanacak. Biletinizin beklentisi $$\left( 490 \times \dfrac{1}{100} \right) + \left( 90 \times \dfrac{2}{100} \right) + \left( 0 \times \dfrac{2}{100} \right) + \left( -10 \times \dfrac{2}{100} \right) = – \dfrac{250}{100}$$dir. Beklenti negatif olduğundan piyango bileti almamak daha mantıklı bir davranıştır.
Konumuz olan oyunun beklentisi kaçtır? Hesaplayalım. 3 lira kaybetme olasılığımız (yani oyundan 1 lirayla kalkma olasılığımız) $1/4$’tür, çünkü $(1, 7, 4)$ durumuna ancak ilk iki atışta üstüste tura gelirse erişebiliriz. (Yukarıdaki şemaya bakınız.) 2 lira kaybetme olasılığımız $1/8 + 1/16$, çünkü $(2, 6, 4)$ durumuna $YTT$ ve $TYTT$ atarak erişebiliriz. Okur tüm olasılıkları hesaplarsa beklentinin, $$ \left( -3 \times \dfrac{1}{4} \right) + \left( -2 \times \dfrac{3}{16} \right) + \left( -1 \times \dfrac{9}{64} \right) + \left( -4 \times \dfrac{27}{512} \right) + \left( 4 \times \dfrac{253}{512} \right) = 0$$ olduğunu bulur. Demek ki bu oyunun beklentisi $0$. Aslında her yazı-tura oyununun beklentisi $0$’dır. Oyuncular oyuna kaç parayla başlarlarsa başlasınlar ve stratejileri ne olursa olsun, yazı-tura oyunlarının beklentisi hep $0$’dır. Bir atışlık yazı-tura oyunlarının beklentisi elbette $0$’dır. Okur bundan yararlanarak her yazı-tura oyununun beklentisinin $0$ olduğunu kanıtlayabilir.
Tavla Üzerine Bir Soru
Önceki bölümde sonlu oyunlardan sözettik. Bu bölümde kuramsal olarak sonsuza dek uzayabilecek, ancak oynandığında, yani uygulamada, bitip bitmeyeceğinden emin olmadığım bir oyundan söz edeceğiz. Hepimizin bildiği bir oyun bu: Tavla.
Tavla sonlu bir oyun mudur? Tavlanın uzun sürdüğü olabilir, ama bugüne dek oynadığınız her tavla oyunu sona ermiştir. Hiç yenişemeden günlerce (bir el) tavla oynayana rastlamamışsınızdır. Oysa tavla sonsuz bir oyundur. Yani kuramsal olarak sonsuza dek sürebilir. Aşağıdaki durumu alalım örnek olarak:
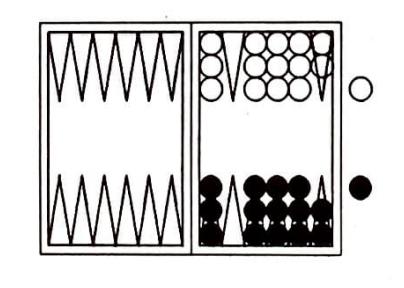
Her iki oyuncunun da birer kırığı var ve her ikisi de penç (5) kapısı dışında bütün kapıları almışlar. Bu durumda her iki oyuncu da durmadan gele atarsa oyun sonsuza dek sürer. Durmadan sonsuza dek gele atmanın, yani hiç penç atamamanın olasılığı -eğer zarlar hileli değilse- sıfırdır. Bu savımın doğruluğunu bir sonraki bölümde kanıtlayacağım. Yani kuramsal olarak sonsuza dek gele atılabilse bile, uygulamada atılamaz. Kuramsal olarak sonsuz olabilen tavla işte bu yüzden uygulamada biter. (Sanıyorum biter, kanıtım yok!)
Buna benzer örnekleri çoğaltabiliriz. İşte bir tane daha:
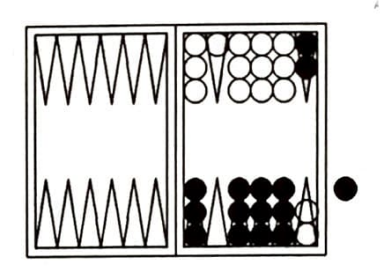
Yukarıdaki durumda her iki oyuncuya da durmadan dübeş (5-5) gelirse oyun sonsuza dek sürer. Bunun olasılığı da sıfırdır elbet.
Tavlanın sonsuza dek sürebileceği durumlara üçüncü bir örnek verelim. Bu örnek yukarıdaki örneklerden değişik olacak; oyuncular isteyerek (ama gene zarın yardımıyla) sonsuza dek sürdürecekler oyunu.

Yukarıdaki oyunda siyahın bir kırığı var ve zar atma sırası siyahta. Dübeş (5-5) geldi. Diyelim, siyah kırık pulu dört kez 5 oynadı; beyazın penç hanesindeki pulu kırıp kendi penç hanesine yattı. Doğru oyun bu değil ama varsayalım siyah böyle oynadı. Şimdi sıra beyazda. Beyaza da dübeş gelsin ve beyaz da kırık taşını dört kez 5 oynasın. Bundan sonra her iki oyuncuya durmadan dübeş gelsin ve yukarıdaki oyunu yinelesinler. Oyun sonsuza dek sürer. Elbet sonsuza dek dübeş gelme olasılığı da sıfırdır.
Tavla -en azından kuramsal ve varsayımsal olarak- çeşitli biçimlerde sonsuza dek sürebilir:
- İlk iki örnekte olduğu gibi oyuncuların bir seçeneği olmayabilir; oyuncular ne oynarlarsa oynasınlar oyun sonsuza değin sürebilir.
- Üçüncü örnekte olduğu gibi oyuncular bilerek ve isteyerek oyunu sonsuza değin sürdürebilirler.
Bir de şu ayrımı yapabiliriz:
a) Her üç örnekte de olduğu gibi oyunun sonsuza dek sürmesi için oyuncular zardan yardım beklerler. Zar istedikleri gibi gelmezse oyun sonsuza dek süremez.
b) Zar ne gelirse gelsin oyun sonsuza değin sürebilir.
İlk iki örnek 1a şıkkının, üçüncü örnekse 2a şıkkının olabileceğini göstermektedir. a şıkkının olasılığı sıfırdır, yani zarların sonsuza değin istediğimiz gibi gelme olasılığı sıfırdır. Dolayısıyla 1b ve 2b şıkları üzerine yoğunlaşmak yeterlidir.
1b şıkkına bir örnek vermeye çalışayım (başaramayacağım, ama deneyeceğim). İki oyuncu da altı kapıyı almış olsalar ve her oyuncunun da birer kırığı olsa, oyun sonsuza dek sürer. Ama tavlada (hile yapmadan) bu duruma erişilemez. Neden erişilmediğinin kanıtını okura bırakıyoruz.
1b ve 2b şıkları tavlada olabilir mi? Bilmiyorum. 1b şıkkının olmaması “gerektiğini” deneyimle biliyoruz. Çünkü oynadığımız bütün tavla oyunları bitmiştir. Tavla genellikle on beş dakikada, bilemediniz bir saatte biter. Tavla oyununun sonlu olduğunu deneyimle biliyoruz. Ancak bunun kanıtını vermedikçe matematiksel kesinlikte tavla oyununun bittiğini söyleyemeyiz. Önsezimiz ve deneyimimiz 1b şıkkının olamayacağını söylüyor. Ama önsezilerimizden öteye gitmeli ve bunun matematiksel bir kanıtını vermeliyiz. Önsezi, matematiğin vazgeçilmez öğelerindendir.
Genellikle, matematikçi kanıtlayacağı teoremden önce kendisi emin olur. Bunun yolu da önseziden geçer. Matematikçi sezgiyle vardığı sonucu daha sonra biçimselleştirmelidir, yani sonucun matematiksel kanıtını bulmalıdır. Öyle ki bu biçimsel kanıtı okuyan hiç kimse kanıtın doğruluğundan en küçük bir kuşku duymamalıdır.
2b şıkkının olamayacağını söylemek pek kolay değil. Bir arkadaşınızla anlaşın ve oyunu bitirmemeye çalışarak tavla oynayın. Örneğin sık sık açık verin. Kazanmak için oynamayın, kaybetmek için de oynamayın. Yalnızca oyunu sonsuza dek sürdürmek için oynayın. Göreceksiniz ki yeterince zamanınız olsa neredeyse başaracaksınız. Bu yazıyı okuyan bir arkadaşım, tavlanın bitip bitmeyeceği sorusunu babasına açmış. Arkadaşımın babası, tavlanın her zaman -her iki oyuncu da kazanmak için oynasa bile- bitmeyeceğine inanabileceğini söylemiş. Çünkü çok uzun süren, hiç de biteceğe benzemeyen ve yarıda bırakmak zorunda kaldığı bir tavla oyunu oynamış.
Yüzde Yüz Sonlu Sonsuz Oyunlar
İkinci bölümde kuramsal olarak sonsuz bir oyun olan tavlanın gerçekten, yani uygulamada, sonsuz olup olmadığı sorusunu sorduk. Şimdi kuramsal olarak sonsuz, ancak uygulamada sonlu bir oyundan söz edeceğiz.
Oyunumuz iki kişi arasında oynanıyor. Yazı-tura atılıyor. Yazı gelirse birinci oyuncu ikinciden 1 lira alıyor, tura gelirse birinci oyuncu ikinciye 1 lira veriyor. Oyunculardan birinin parası bittiğinde oyun da bitiyor. Eğer iki oyuncunun da oyuna başlarken ikişer lirası varsa ve sürekli bir yazı bir tura gelirse oyun sonsuza dek sürer; çünkü bu yazı-tura atışlarıyla oyunculardan birinin parası bitmez. Öte yandan bu oyunu ne zaman oynarsanız oyun biter! Hatta oldukça çabuk biter, bir dakika sürmez bile. Neden? Hiç durmadan bir yazı bir tura gelme olasılığı çok zayıftır da ondan. Bu yazıda bunu kanıtlayacağız. Kuramsal olarak sonsuza dek sürebilen bu oyun, uygulamada sonsuza dek süremez. Çünkü bu oyunun sonsuza dek sürebilme olasılığı öyle küçük, öyle küçüktür ki… sıfıra eşittir. Bu olguyu kanıtlamadan önce biraz eğleneceğiz. Eğlence matematiğin önemli öğelerinden biridir, savsaklamaya gelmez. Yeterince eğlendikten sonra bu olgunun matematiksel kanıtını vereceğiz.
Oyunu daha iyi anlamak için oyunun ağacını bulalım. Oyun $(2,2)$ durumu ile başlıyor. Yani başlangıçta her iki oyuncunun da ikişer lirası var. Diyelim biz birinci oyuncuyuz ve yazı gelince kazanıyoruz. Ağacın tepesine $(2, 2)$ yazalım. Para atıldı. İki olasılık var: ya tura gelecek kaybedeceğiz ya da yazı gelecek ve kazanacağız. Kaybedersek oyunun yeni durumu $(1,3)$ olacak, yani bizim 1 liramız, öbür oyuncununsa 3 lirası olacak. Bu $(1, 3)$ durumunu ağacın soluna yazalım. Kazanırsak $(3,1)$ durumuna erişeceğiz. Bunu da ağacın sağına yazalım. Ağaş sağlı sollu kök salar. Soluna kaybettiğimizde, sağınaysa kazandığımızda erişeceğimiz durumu yazarız. $(3, 1)$’den sonra gene iki durum ortaya çıkabilir: $(2, 2)$ ve $(4, 0)$ durumları. $(2, 2)$’yi sola, $(4, 0)$’ı sağa yazalım. $(4, 0)$ durumunda oyun biter ve kök salmaz. $(2, 2)$ durumundaysa oyun sürer. İşte oyunun ilk dört aşamasını gösteren ağaç:
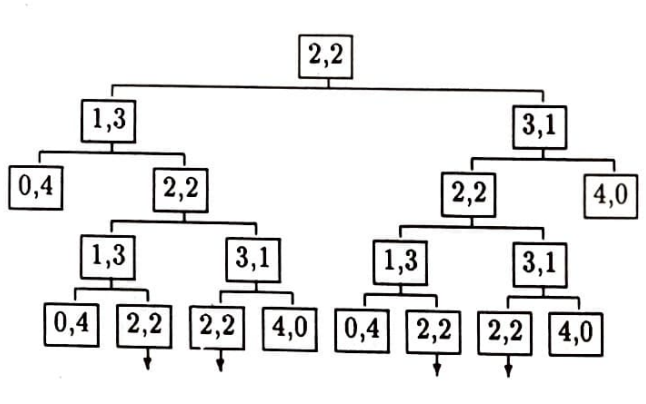
Oyun ancak $(4, 0)$ ve $(0, 4)$ durumlarından birine geldiğinde biter, öbür durumlarda sürer. Bu yüzden dördüncü aşamadaki $(2,2)$ durumlarında ağaç kök salmayı sürdürür. Bu ağaç sonsuz bir ağaçtır. Köklerden bazıları bitse bile, köklerin kökü kurumaz. Ağaç sonsuzdur, çünkü oyun sonsuzdur. Örneğin, $(2,2)$, $(1,3)$, $(2,2)$, $(1,3)$,… diye durmadan sonsuza dek uzayıp giden bir kök vardır.
Oyunun sonsuz olduğunu göstermek için illa sonsuz bir ağaç yapmaya gerek yoktu. Sonlu bir şemayla da bu sonsuz oyunun gidişini gösterebiliriz. Bu şemayı çizelim. Oyunda beş durum var: $$(0,4),\ (1,3),\ (2,2),\ (3,1),\ (4,0)$$ durumları. Bu beş durumu birer kare içine alalım. Bir durumdan öbür duruma nasıl geçildiğini bir okla gösterelim. Eğer bir durumdan öbür duruma kazanarak geçebiliyorsak, okun kenarına $1$ koyalım. Kaybederek geçebiliyorsak $0$ koyalım. Örneğin, $(1,3)$ durumundan $(2,2)$ durumuna kazanarak geçebildiğimizden, $(1,3)$ durumundan $(2,2)$ durumuna giden oka $1$ adını veririz. İşte bu oyunun şeması:
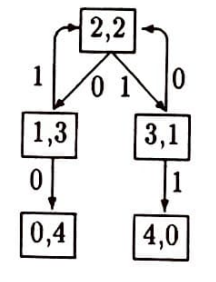
$(0,4)$ ve $(4,0)$ durumlarında oyun bittiğinden bu iki durumdan ok çıkmaz. Bu şemaya bakarak oyunun sonsuz olduğunu nasıl anlarız? Eğer bir kısır döngü (yani bir çember) varsa oyun sonsuz demektir. $(2,2)$ durumundan başlayarak ve okları izleyerek ya $(4,0)$ ya da $(0, 4)$ durumlarına gelmek zorunda değilsek oyun bitmez. Örneğin $(2,2)$’yle $(1,3)$ arasında bir kısır döngü vardır. Bunun gibi $(2,2),\ (1,3),\ (2,2),\ (3,1),\ (2,2),\ (1,3),…$ döngüsü de döner durur.
Ağacımıza geri dönelim. Ağaca alıcı bir gözle baktığımızda oyunun birinci ve üçüncü yazı-tura atışlarından sonra bitmediği anlaşılıyor. Biraz düşünürsek, oyunun tek sayılı yazı-tura atışlarından sonra bitmeyeceğini görürüz (örneğin tümevarımla). Oyun 2, 4, 6 gibi çift sayılı atışlardan sonra bitebilir ancak.
Oyunun ikinci yazı-tura atışında bitme olasılığını bulalım. Paranın hileli olmadığını varsayıyoruz; yani yazı gelme olasılığı $1/2$, tura gelme olasılığı $1/2$. Ağacın ikinci kuşak köklerine bakalım. Dört dal var. Her birinin olasılığı $1/4$’tür, çünkü ikinci kuşaktaki $(0,4),\ (2,2),\ (2,2)$ ve $(4,0)$ durumlarına ancak $TT$ (tura tura), $TY$ (tura yazı), $YT$, $YY$ atıldığında erişebiliriz. Bu dört durumdan ikisinde oyun bitiyor ikisinde bitmiyor. Dolayısıyla, ikinci yazı-tura atılışında oyunun bitme olasılığı $1/4 + 1/4$, yani $1/2$’dir. Şimdi oyunun en fazla dördüncü yazı-tura atışında bitme olasılığını bulalım. Ağaca bakarak, oyunun en fazla dört yazı-tura atışında nasık bitebileceğini buluruz: $$TT,\ TYTT,\ TYYY,\ YTTT,\ YTYY,\ YY$$ atıldığında oyun biter. Bu 6 yazı-tura atışının (olayın) olasılıkları sırasıyla şöyle: $$1/4, 1/16, 1/16, 1/16, 1/16, 1/4.$$ Dolayısıyla, oyunun en fazla dört yazı-tura atışında bitirme olasılığı bu sayıların toplamıdır, yani $3/4$’tür. Oyunun en fazla altı yazı-tura atışında bitme olasılığını hesaplayalım. Yukarıdaki apacı sürdürecek olursak, altıncı aşamada 4 tane $(0,4)$ ve 4 tane $(4,0)$ olduğunu görürüz. Oyunu sona erdirecek bu 8 kökten her birine ulaşma olasılığı $1/2^{64}$, yani $1/64$. Dolayısıyla oyunu bitiren bu 8 kök uçlarından birine ulaşma olasılığımız $8/64$, yani $1/8$. Bu olasılığı bir önceki paragrafta bulduğumuz $3/4$ olasılığına ekleyecek olursak oyunun 6 ve daha az yazı-tura atışında bitme olasılığını buluruz. Demek ki, oyunun en fazla 6 yazı-tura atışında bitme olasılığı $$ 3/4 + 1/8 = 7/8$$dir. İkinci, dördüncü ve altıncı yazı-tura atışlarından önce oyunun sona erme olasılıklarını sırasıyla $$1/2,\ 3/4,\ 7/8$$ olduğunu bulduk. Okuz, oyunun en fazla sekiz yazı-tura atışında bitme olasılığını hesaplarsa $15/16$ bulacaktır.
Bir oyuncuda $A$ lira, öbür oyuncuda $B$ lira olsun. Oyunun hangi aşamasında olursak olalım, üstüste $A + B$ kez yazı atıldığında oyunculardan birinin parası biter, hatta daha önce de bitebilir. Demek ki eğer $1$ olasılıkla üstüste $A+B$ kez yazı atacağımızı kanıtlarsak, bütün yazı-tura oyunlarının $1$ olasılıkla sonlu bir zamanda biteceğini kanıtlamış oluruz. Dolayısıyla şu teoremi kanıtlamalıyız:
Teorem. $n > 0$ herhangi bir tamsayı olsun. Sonsuz kez yazı-tura atıldığında üstüste $n$ kez tura gelme olasılığı $1$’dir, yani yüzde yüzdür.
Bu teorem, tura gelince kazananın oyunu kazanacağı anlamına gelmez. Üstüste $A+B$ kez tura gelecektir ($1$ olasılıkla). Orası kesin. Üstüste $A+B$ kez de yazı gelecektir. O da kesin Ama hangi oyuncu daha önce kaybedecektir? Orası kesin değil. Şansa bağlı. Gelecek yazıda hangi oyuncunun kaç olasılıkla oyunu kazanacağını bulacağız.
Teoremin Kanıtı. Ardarda $n$ kez yazı-tura atıldığında hep tura gelme olasılığı $1/2^n$’dir. Dolayısıyla $n$ yazı-tura atışının hepsinin birden tura olmama olasılığı $1 – 1/2^n$’dir. Bu sayıya $\alpha$ diyelim: $$\alpha = 1 – 1/2^n.$$
$0 \leq \alpha < 1$ eşitsizlikleri birazdan önem kazanacak, aklımızın bir köşesinde tutalım.
Şimdi $2n$ kez yazı-tura atalım. $2n$ yazı-tura atışında $n$ kez üstüste tura gelme olasılığına $\beta_2$ diyelim. $\beta_2$ sayısını bulmak kolay olmayabilir, ama bu sayının $1-\alpha^2$’den büyük olduğunu kanıtlayabiliriz. $2n$ atışta nasıl üst üste $n$ kez tura gelebilir? Çeşitli biçimlerde gelebilir. Örneğin ilk $n$ atış salt tura olabilir ya da son $n$ atış salt tura olabilir. Ne birinci $n$ atışın ne de ikinci $n$ atışın salt tura olmama olasılığı $\alpha^2$’dir. Demek ki ya birinci $n$ ya da ikinci $n$ atışta salt tura gelme olasılığı $1-\alpha^2$’dir. Dolayısıyla $2n$ atışta $n$ kez üstüste tura gelme olasılığı en az $1-\alpha^2$’dir. Yani $$1-\alpha^2 \leq \beta_2 \leq 1$$ eşitsizlikleri geçerlidir.
Yukarıdaki akıl yürütmeyi $3n$, $4n$ ve genel olarak $kn$ atış için yapabiliriz. Şöyle yaparız: $k > 0$ bir doğal sayı olsun ve $kn$ kez yazı-tura atalım. $\beta_k$, $kn$ atışta üstüste $n$ kez tura gelme olasılığı olsun. $$(3) \quad \quad 1-\alpha^k \leq \beta_k |\leq 1$$ eşitsizliklerini kanıtlamak istiyoruz. $\beta_k \leq 1$ eşitsizliği elbette doğru. Birinci eşitsizliğe bakalım. Ne ilk $n$ atışın ne de $k$’yinci $n$ atışın salt tura olmama olasılığı $\alpha^k$’dir. Dolayısıyla bu $k$ tane $n$ atıştan birinde (ya birinci, ya ikinci,… ya da $k$’yinci $n$ atıştan birinde) salt tura gelme olasılığı $1 – \alpha^k$’dir. Dolayısıyla $kn$ atışta üstüste $n$ kez tura gelme olasılığı $1-\alpha^k$’dan fazladır. Yani $1-\alpha^k \leq \beta_k$ eşitsizliği geçerlidir. $(3)$’ü kanıtladık.
$0 < \alpha < 1$ eşitsizliklerinden dolayı, $k$ sonsuza gittiğinde $a^k$ sayısı sıfıra yakınsar (yaklaşır, gider) ve $1 – \alpha^k$ sayısı bire yakınsar: $$\lim_{k \to \infty} (1- \alpha^k) = 1.$$
$(3)$ eşitliğinde $k$’yi sonsuza götürürsek, $$1 = \lim_{k \to \infty} (1- \alpha^k) \leq lim_{k \to \infty} \beta_k \leq 1$$ elde ederiz ki, bu da, $k$ sonsuza gittiğinde $\beta_k$ sayılarının bire yakınsadığını gösterir. Demek ki atış sayımız yükseldikçe $n$ kez ardarda tura atma olasılığımız bire yakınsıyor. Teoremimiz kanıtlanmıştır.
Üstteki kanıtta atılan paranın hilesiz olduğunu pek kullanmadık. Para hileli bile olsa, tura gelme olasılığı sıfırdan büyükse, her $n$ için, sonsuz yazı-tura atışında üstüste $n$ kez tura gelme olasılığı $1$’dir. Bunun kanıtı da yukarıdaki teoremin kanıtı gibi.
$^1$Bu güzel kanıt için Sinan Sertöz’e teşekkür ederim.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 4. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep Begüm Kara‘ya ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

