Yazar: Alp Eden (alp.eden5@gmail.com)
Yıl: 2022-2
Sayı: 112

Kastamonu Lisesi’nden mezun olan Süleyman Sencer (29.01.1912 – 01.06.1947) 1932-1933 yılında Lüben’de dil öğrendikten sonra Berlin ve Leipzig üniversitelerinde matematik okuyor ve matematik doktora tezini 23 Haziran 1938 yılında Leipzig Üniversitesinde savunuyor. Ankara Üniversitesi’nde doçentliğe kadar yükselen Süleyman Sencer, genç yaşında aramızdan ayrılıyor. Hollandalı matematikçi ve bilim tarihçisi Bartel Leendert van der Waerden’in danışmanlığı altında tamamladığı doktora tezinin günümüzde de gündeme gelmiş olması bu yazıyı yazmama ön ayak oldu. Tezini kısmen de olsa tarihsel bir perspektife oturtmaya çalıştım.
Hilbert’in Alanlar için Aksiyom Sistemi
David Hilbert Geometrinin Temelleri kitabında (düzlemde) Öklid Geometrisi için bir aksiyom sistemi önerir. Bu aksiyomlar beş başlık altında verilir: Konum (Incidence) Aksiyomları (7 tane); Sıralama (Order) Aksiyomları (5 tane); Paralellik Aksiyomu; Eşlik (Congruence) Aksiyomları (6 tane); Süreklilik Aksiyomları (2 tane). (bkz. http://math.cu.edu.tr/Dersler/MTS221/HilbertAksiyomlari.pdf)
Hilbert’in aksiyom sistemi içinde göze çarpan ve geometriyle alakası hemen kurulamayan süreklilik aksiyomlarından Arşimed Aksiyomu ve Tamlık (Completeness) Aksiyomu geometriden çok reel sayı sistemine ait aksiyomlar gibi dururlar. Daha saf bir geometrici için onların aksiyom sisteminde varlığı doğal değildir.
Tüm matematiğin temellendirilmesiyle ilgili büyük bir araştırma projesinin altına imza atmış olan David Hilbert’in 1899 yılında Leipzig’de yayımlanmış bu kitabı, matematiğin temellendirme çalışmaları için iyi bir örnek teşkil eder.

19. yüzyılda, paralellik aksiyomunun geçerli olmadığı, Öklid-dışı geometriler matematiğin gündemine oturmuş ve bu aksiyomun geçerliliğinin derinden sorgulanmasına neden olmuştur. Dolayısıyla Hilbert’in kitabında da paralellik aksiyomunun diğer aksiyomlara göre statüsünün (bağımsızlığının) incelenmesi önemli bir yer tutar. Ayrıca kitapta başka ve daha sınırlı aksiyomatik sistem örnekleri de verilir. Burada bu daha kısıtlı sistemlerden biri üzerine yapılmış bazı çalışmalardan bahsedeceğim.
Kitabının dördüncü bölümünde Hilbert düzlemde alan ölçümlerini tanımlamaya yönelik bir aksiyom sistemi önerir. Bu aksiyom sistemi içinde Arşimed aksiyomu yer almaz. Diğer bir deyişle Hilbert’in bu bölümde düzlem alan ölçümleriyle ilgili elde ettiği neticeler Arşimed aksiyomundan bağımsızdır.
Hilbert’in kitabının değişik baskıları yapılır, ölümünden sonra çalışma arkadaşı Paul Bernays, kitaptaki konularda yaşanan gelişmeleri bölüm sonlarındaki eklerde anlatır. Yazımda Bernays’ın 1968 yılında yayımladığı ve Leo Unger’in çevirdiği Foundations of Geometry başlıklı İngilizce baskısını temel alacağım (Hilbert (1971)).
Alan ölçümlerinin aksiyomatik incelenmesinde eşbölünebilirlik kavramı önemli bir rol oynar. Eğer iki poligon sonlu sayıda ama aynı sayıda ve biçimde olan üçgenlerin değişik konumlandırılmalarıyla bir araya getirilip, yapıştırılmasıyla oluşturulabiliyorsa, bu poligonlara eşbölünebilir poligonlar denir (Hilbert (1971) sayfa 60). Hilbert kitabında poligonların alanları için eşbölünebilirlik kavramının alanların eşitliğiyle örtüştüğünü gösterir. Yani eşbölünebilir poligonların alanları birbirine eşit olduğu gibi, alanları eşit iki poligon da eşbölünebilir poligonlardır.
Benzer bir tanım hacimsel ölçümler için de yapılabilir. Burada ilk aşamada hem poligonların hem de üçgenlerin yerini tetrahedralar (dört üçgen yüzlüler) alır. Ama burada farklı bir durum karşımıza çıkar. Aksiyom sistemi vasıtasıyla tanımlanmış olan alan kavramını benzer bir biçimde uzay ve hacim kavramına taşırken bazı zorluklar belirir. Hilbert’in üçüncü problemi olarak bilinen problem ve onun çözümü bu zorluklara güzel bir örnek teşkil eder.
Hilbert’in üçüncü problemi
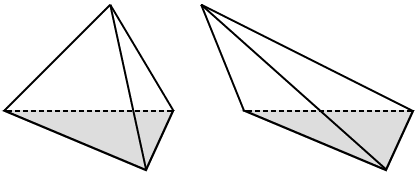
İki tane dört üçgen yüzlü cisim (tetrahedra) verilmiş olsun. Bu dörtyüzlülerin taban alanları ve yükseklikleri eşit olsun. Yani bu cisimlerin hacimleri birbirine eşit olsun. O zaman, bu dörtyüzlülerin her ikisini de aynı sayıda küçük dörtyüzlülere ayrıştırarak, sonra bu iki grubu ayrı ayrı birleştirerek
eşbölünebilir iki çok yüzlü elde edilebilir mi? Yani eşbölünebilirlik eş hacim için yeterli bir koşul olduğu kadar, gerekli bir koşul mudur?
Bu sorunun olumsuz cevabı bir örnekle 1900 yılında Hilbert’in doktora öğrencisi Max Dehn tarafından verilir (bkz. Hilbert (1971)).
David Hilbert’in Türkiye’deki en büyük savunucularından biri olan Kerim Erim, Mühendis Mektebi Mecmuası‘nda 1932 yılında yayımlanan yazısında Hilbert’in yirmi üç problemini tanıtır. Bu problemleri Hilbert, 1900 yılında Paris’te toplanan Uluslararası Matematikçiler Kongresi’nde (ICM) verdiği bir konuşmada kısmen sunmuştur. Hilbert’in konuşmasının metni bildiri kitapçığında yayımlandığında açık problem sayısı yirmi üçe çıkmıştır (İngilizce tercümesi için bkz. Hibert (1902)). Hilbert’in problemleri 20. yüzyılın başında matematikçileri oldukça meşgul eder. Yukarıda adı geçen üçüncü problem de bu listedeki problemlerden biridir.
Kerim Erim üçüncü problemi, biraz muğlak bir biçimde, şöyle ifade eder:
Gerling çok vecihli ve mütenazır (çokyüzlü ve simetrik) olan hacimlerin müsavatını müsavi parçaları ayırarak ispat etmiştir. Fakat Hilbert’e nazaran evvelce zikredilen Euklid davasının ispatı gayri mümkün gözüküyor. Bu takdirde bu meselenin gayri mümkün olduğunu ispat etmek mevzuu bahistir. (bkz. Bahadır (2006) sayfa 137.)
Van der Waerden’in iki öğrencisi Sencer ve Frei
Hilbert’in alan ölçümleri için önerdiği aksiyom sisteminin benzerlerini hacimlere genişletmek doğal bir araştırma alanıdır. Bu konuda katkıda bulunan matematikçilerden biri de Hollandalı matematikçi B. L. van der Waerden’dir. 1925 yılında Hollandaca yazdığı De Logische Grondslagen der Euklidische Meetkunde adlı kitabında van der Waerden Hilbert aksiyomlarına farklı bir yaklaşım getirir.
1938 yılında Çankırı’nın Kurşunlu kazasından Süleyman Sencer matematik doktora tezini Leipzig Üniversitesi’nde van der Waerden ve Koebe’nin danışmanlıkları altında tamamlar. Aşağıda Süleyman Sencer’in doktora tezinin kapak sayfasının fotoğrafı var.

Süleyman Sencer tezinde hacim ölçümleri için iki farklı aksiyom sistemi önerir. Yazımda bunlardan sadece ikincisine odaklanacağım. Bu aksiyom sistemini doktora tezinde şöyle verir Sencer:

Sencer’in aksiyom sistemlerinin daha basitleşebileceği konunun uzmanlarından Bachmann’ın JFM (Jahrbuch über die Fortschritte der Mathematik) için yazdığı tez değerlendirme yazısında belirtilir (JFM 64.1262.01). Bu sadeleştirmeleri van der Waerden’in bir başka doktora öğrencisi Günther Frei’ın 1968 yılında Zürih’te tamamladığı doktora tezinde gerçekleştirir. Frei tezinden çıkardığı makalede tezinin Sencer’in aksiyomlarına ne kadar dayandığını tekrar tekrar söyler. Burada Frei’ın önerdiği sadeleştirmelerden ikincisini vereceğim (Frei (1970)).
Aşağıda “eşitlik” cisimler için “hacimlerin eşitliği” anlamında kullanılmıştır. Cisimler arasındaki eşitsizlik ilişkileri de $P > Q$ ve $P < Q$ gibi, “hacimlerin kıyaslamasına'” dayanır. İki çokyüzlünün toplamı onların içindeki noktaların toplamı olarak tanımlanır. Yani $P+Q = \{ x + y\, |\, x \in P,\, y \in Q\}$.
Sencer-Frei aksiyom sistemi
(S 1) $P > Q$, $P < Q$ ve $P = Q$ ilişkileri birbirlerini dışlarlar.
(S 2) Eşlenebilirlik/eşbölünebilirlik ($=$) ilişkisi geçişlidir (transitive).
(S 3) Eğer $P + Q = P’+ Q’$ ve $Q = Q’$ ise o zaman $P = P’$ olur.
(S 4) Eşbölünebilir çokyüzlüler (polyhedra) birbirine eşittir.
(S 5) $P = Q + R$ ilişkisinden $P > Q$ çıkar.
(S 6) Eğer $P > Q$ ise o zaman öyle dörtyüzlü bir piramid $R$ vardır ki $P = Q + R$ olur.
(S 7) Herhangi iki çokyüzlü $P$ ve $Q$ için ya $P > Q$ ya $P < Q$ ya da $P = Q$ ilişkilerinden birisi geçerlidir. (Frei (1970) sayfa 221)
Çok yakın zamanda Sencer-Frei aksiyom sistemleri tekrar hatırlandı (bkz. Giovannini, E., Haeusler, E., Lassalle-Casanave, A., & Veloso, P. (2019). “De Zolt’s Postulate: an Abstract Approach” The Review of Symbolic Logic, 1-28. ve Giovannini, E.N. “David Hilbert and the foundations of the theory of plane area” Arch. Hist. Exact Sci. (2021)). Sencer-Frei aksiyom sistemlerinin bilim tarihinde kendilerine bir köşe edindiklerini söyleyebilirim.
Sencer’in Doktora Tezi
Sencer’in 35 sayfalık doktora tezi 8 bölümden oluşur. İlk bölümde iki aksiyom sistemi tanıtılır. Bu aksiyomlar yardımıyla paralelyüzlü (paralellepiped) cisimler ve prizmalar ve dörtyüzlülerin ölçümleriyle ilgili bazı neticeler ispatlanır. Aynı taban ölçümüne ve aynı yüksekliğe sahip iki dört üçgenyüzlü (tetrahedra) hacim ölçümlerinin de aynı olduğu ispatlanırken çokyüzlüler için Arşimed aksiyomunun geçerliliği farz edilir. Burada düzlem alanla ilgili bir fark da ortaya çıkmış olur. Yukarıda belirttiğim gibi Hilbert alan ölçümleri için benzer bir neticeyi Arşimed aksiyomunu kullanmadan elde edebilmiştir.

Sencer tezinde çokyüzlülerin bir Arşimet boyut sistemi oluşturduğunu ve Öklid orantısal eşitlik tanımının yardımıyla bir orantı teorisinin oluşturulabileceğini gösterir. Yani her çokyüzlüyü bir sayı olarak düşünüp, bu sayıların arasındaki orandan söz etmenin mümkün olduğunu gösterir. Ayrıca bir paralelyüzlü cismin ölçümünün taban çarpı yüksekliğe eşit olduğunu ispatlar. Benzer neticeleri prizmalar ve dörtyüzlüler için de ispatlar. Son bölümdeyse bu şekilde tanımlanan hacim ölçümünün Riemann anlamında içerikle uyumlu olduğunu kanıtlar. Doğallıkla Frei’ın önerdiği ve Sencer’in sistemine denk olan Sencer-Frei aksiyom sisteminden de Sencer’in neticelerini elde etmek mümkündür.
Süleyman Sencer kimdir?

Yukardaki metin Süleyman Sencer’in doktora tezinin sonunda verdiği özgeçmişidir (Lebenslauf). Bu sayfadan şu bilgileri elde ediyoruz:
Çankırı’nın Kurşunlu ilçesinde 29 Ocak 1912 yılında doğdum. Babam tüccar Ömer Sencer, liseyi Kastamonu’da 1932 yılında tamamladım. Kazandığım devlet bursuyla Lüben’de bir yıl Almanca öğrendim. Berlin Üniversitesi’nde matematik, fizik ve astronomi derslerini takip ettim. Hocalarım arasında Bieberbach, Feigl, Klose, Kopff ve Wehnelt de vardı. 1934 yılının Kasım ayında Leipzig Üniversitesi’ne geçtim. Orada Debye, Heisenberg, Hopf, Hopmann, Hölder, Hund, Koebe, Schnee ve van der Waerden gibi profesörlerin derslerine ve seminerlerine katıldım. 1938 yılında doktoramı Koebe ve van der Waerden danışmanlıkları altında tamamladım.
Süleyman Sencer hakkındaki bilgilerimin yakın zamana kadar çok sınırlı kaldığını belirtmeliyim. Lüben’deki dil okulu mezunları hakkında verilen çevirimiçi bilgi yukarıdaki özgeçmişinde de var. Doktora tezinin kopyaları Millî Kütüphane’de olduğu gibi ikinci el kitapçısı AbeBooks’tan da temin edilebiliyor. Doktora tezinin başlığına Erdal İnönü matematik bibliyografya çalışmasında yer veriyor. Ayrıca Ankara Fen Fakültesi’nin bir numaralı öğrencisi olan Erdal İnönü’nün hocası da olmuş kendisi.
Ankara Üniversitesi’nde doçent kadrosuna yükselmiş olduğunu ne yazık ki trajik bir biçimde öğreniyoruz. Ankara Üniversitesi rektörlerinin açılış konuşmalarında (Atılgan (2003) sayfa 29) Rektör Şevket Aziz Kansu 1947-1948 öğretim yılı açılış konuşmasında Doç. Dr. Süleyman Sencer’in 01.06.1947 tarihinde öldüğünü bildiriyor.

155 Süleyman, ortadaki resim.
Süleyman Sencer’in Kastamonu Lisesi’nden mezun olmuş olması ve lisesiyle irtibatını sürdürmesi onun hakkında bazı arşiv bilgilerine ulaşabilmemi sağladı. Onun resimleri bu arşivden geliyor. Kastamonu Abdurrahman Paşa Lisesi bünyesinde yakında açılacak bir müzede sözü geçen arşivlerden örnekler sergilenecek.
Teşekkür.
Öncelikle Süleyman Sencer’in doktora tezinin dijital kopyasını temin eden Murat Sağlam’a teşekkür ederim. Yardımları, arşiv bilgileri ve resimler için, Kastamonu Abdurrahman Paşa Lisesi Müdürü Hüseyin Mısırlıoğlu başta olmak üzere Kastamonu Eğitim Fakültesi Dekanı Prof. Dr. Ahmet Kaçar’a ve Semiha Betül Takıcak’a teşekkür ederim. Yazıyı okuyup öneriler yapan Murat Sağlam, Türker Bıyıkoğlu ve Ersin Karabudak’a teşekkür ederim.
Kaynaklar
[1] Atılgan, D. (editör) (2003) Cumhuriyetimizin 80. Yılında üniversitemizin dünü, bugünü ve geleceğe bakışı rektörlerimizin eğitim yılı açış konuşmaları 1946-2004 [çevirim içi kaynak], Ankara, Kütüphane ve Dokümantasyon Daire Başkanlığı, Ankara Üniversitesi Yayınevi, 450 sayfa.
[2] Bahadır, Osman (2006) Matematikte bir öncü: Kerim Erim, Anahtar Yayınları, İstanbul.
[3] Frei, G. (1970) “Beiträge zur axiomatischen Inhaltstheorie.” Math. Ann. 187, s. 220-240.
[4] Hilbert, D. (1902) “Mathematical problems”, Bull. Amer. Math. Soc. 8, 437-479.
[5] Hilbert, D. (1971) Foundations of Geometry, Çeviren. Leo Unger, genişletilmiş ve düzeltilmiş baskıyı (1968) derleyen Paul Bernays, dördüncü baskı 1988, Open Court Publishing Company, La Salle, Illinois.
[6] Sencer, S. (1938) Axiomatische Theorie der Rauminhalte, Danışmanlar. Bartel Leendert van der Waerden ve Paul Koebe, 38 Sayfa, 11 şekil (Doktora Tezi 1938 Leipzig).
[7] Lüben Dil Okulunun Mezunları sitesi: http://www.lueben-damals.de/erinnerungen/gruppenbilder/tuerken.html

