Yazar: Ali Nesin
Yıl: 1992-5
Sayı: 5
Olasılık hesaplarıyla günlük yaşamımızda karşılaşırız. Örneğin tavla yada kağıt oyunları oynarken. İki kapıya üstüste gele atmayan tavlacı görmedim hiç. Şansızlık deriz. Elbet, dört kez gele atan, üç kez gele atandan daha şanssızdır. Bu yazının amaçlarından biri de, “daha şanssız” sözcüğüne matematiksel anlam kazandırmak olacak.
Elimize bir zar alalım. Altı yüzlü hilesiz bir zar… Her sayının gelme olasılığı aynıdır: $1$ sayısının gelme olasılığı, $2$ sayısının gelme olasılığından fazla değildir. Zarın altı yüzü olduğundan, ve her sayının gelme olasılığı aynı olduğundan, örneğin $1$ sayısının gelme olasılığına $1/6$ demek mantıklı olur. Eğer $i=1, …, 6$ herhangi bir sayıysa, $o(i), i$ sayısının gelme olasılığı olsun. Sezgilerimize dayanarak yazalım:
$o(1)=1/6, o(2)=1/6, …, o(6)=1/6.$
Zar hilesiz olduğundan, $o(7)=0$ da yazabilirdik! Tüm olasılıkların toplamının $1$ olduğuna dikkatinizi çekerim. (Günlük yaşamda olasılıklar $100$ üzerine hesaplanır, ama matematikte en büyük olasılık $1$’dir. Günlük yaşamda kullanılan $%75$’in matematikçesi $3/4$ olasılığıdır.)
Çift bir sayı atma olasılığını bulalım şimdi; yani, $2, 4, 6$ sayılarından birinin gelme olasılığını. Her sayının gelme olasılığı 1/6 olduğundan, çift sayı gelme olasılığı $o(2) + o(4) + o(6)=1/6 + 1/6 + 1/6 =1/2$’dir. Ve elbet, tek sayı gelme olasılığı da $1/2$’dir.
Olasılık teoricileri, yukarıdaki sorunda ortaya çıkan $\{ 1, 2, 3, 4, 5, 6\}$ kümesine olaylar kümesi derler. Örneğin, $1$ bir olaydır, ve $1$ olayının gerçekleşme olasılığı $1/6$’dir.
Şimdi işleri biraz zorlaştıracağız ve iki (hilesiz) zar atacağız. İlk önce iki zarı birbirinden ayıralım: zarlardan birine birinci zar, öbürüne ikinci zar diyelim (dilerseniz zarları boyayın). Her iki zarın da altışar yüzü olduğundan, otuzaltı “olay” var:
| $1-1$ | $1-2$ | $1-3$ | $1-4$ | $1-5$ | $1-6$ |
| $2-1$ | $2-2$ | $2-3$ | $2-4$ | $2-5$ | $2-6$ |
| $3-1$ | $3-2$ | $3-3$ | $3-4$ | $3-5$ | $3-6$ |
| $4-1$ | $4-2$ | $4-3$ | $4-4$ | $4-5$ | $4-6$ |
| $5-1$ | $5-2$ | $5-3$ | $5-4$ | $5-5$ | $5-6$ |
| $6-1$ | $6-2$ | $6-3$ | $6-4$ | $6-5$ | $6-6$ |
Dikkat ettiyseniz, $1-2$ ve $2-1$ zarlarını (yani olaylarını) ayrı yazdım, yani iki ayrı olay olarak gösterdim. Çünkü iki zarı birbirinden ayırıyorum: birinci zar $1$ sayısını, ikinci zar $2$ sayısını gösteriyorsa, gelen zara $1-2$ diyorum, tam tersiyse $2-1$. Zarlar hilesiz olduğundan, her olayın gerçekleşme olasılığı aynı. Dolayısıyla, $o(i-j)$ sayısı, $i-j$ olayının gerçekleşme olasılığıysa, $o(i-j)=1/36$’dır. Örneğin, $o(1-1)=o(1-2)=o(2-1)=o(3-4)= 1/36$’dır, Bunu şöyle de gösterebiliriz. Zar atacağımıza, yukarıdaki tabloya rasgele bir taş atalım, $36$ hücre olduğundan, ve bir hücrenin öbür hücreye göre bir özelliği olmadığından, taşın, örneğin $3-4$ hücresine düşme olasılığı $1/36$’dır.
Oysa tavlada zarlar birbirinden ayırdedilmez. Biz de ayırdetmeyelim. O zaman, $1-2$ ve $2-1$ zarlarını da ayırdetmememiz gerekir, bu iki olayı $(1, 2)$ olarak gösterelim. Olayları yukarıdaki gibi sıralayım (yukarıdaki tabloyu ikiye katlayarak):
| $ (1, 1)$ | $(1, 2) $ | $(1, 3)$ | $(1, 4)$ | $(1, 5)$ | $(1, 6)$ |
| $(2, 2)$ | $(2, 3) $ | $(2, 4)$ | $(2, 5)$ | $(2, 6)$ | |
| $(3, 3)$ | $(3, 4)$ | $(3, 5)$ | $(3, 6)$ | ||
| $(4, 4) $ | $(4, 5)$ | $(4, 6) $ | |||
| $(5, 5) $ | $(5, 6) $ | ||||
| $(6, 6)$ |
$21$ olayımız var. Ama bu kez her olayın olasılığı aynı değil. Örneğin $(1, 2)$ olayının olasılığı $1/36 + 1/36=2/36$, çünkü $(1, 2)$ zan için, $1-2$ ya da $2-1$ gerekli:
$o(1, 2)=o(1-2)+o(2-1)=1/36+ 1/36=2/36$.
Öte yandan, $(1, 1)$ zannın gelme olasılığı $1/36$. Demek ki, eğer $i \neq j$ ise,
$o(i, j)=2/36$
dir, ve
$o(i, i)=1/36$
dir. (Özellikle $2/36$ yerine $1/18$ yazmıyoruz, ileride kolaylık olacak). Alıştırma olarak, çeşitli olasılıklar hesaplayalım.
İki kapıya gele atma olasılığı. Bu kapıların $1$ ve $2$ kapıları olduğunu varsayalım. Demek ki $(1, 1), (1 , 2)$ ya da $(2, 2)$ atma olasılığını hesaplayacağız. Buda $o(1, 1) +o(1, 2) + o(2, 2)=1/36 +2/36 + 1/36=4/36 = 1/9$’dur. İki kez iki kapıya gele atma olasılığıysa $1/9$ X $1/9 = 1/81$’dir. Yedi kez iki kapıya gele atma olasılığı ise $(1/9)^7$’dir. (Aşağı yukarı, piyangoda en büyük ikramiye çıkma olasılığına eşit!)
1 atma olasılığı.
$o(1, 1) + o(1, 2) + …+ o(1, 6) + )= \frac{1}{36}+5 x \frac{2}{36}= \frac{11}{36}$
Demek ki, $1$ atma olasılığı $1/3$’ten biraz daha az.
4 atma olasılığı. Yukarıdaki gibi hesaplanır ve $11/36$ bulunur.
Dört hane ilerideki bir pulu kırma olasılığı. Dört hane ilerideki pulu kırmak için ya $4$ atmak gerekir ya $(1, 1)$, ya $(1, 3)$, ya da $(2, 2)$. Demek ki pulu kırma olasılığı
$11/36 + o(1, 1) + o(1, 3) + o(2, 2)= 11/36 + 1/36 + 2/36 + 1/36= 15/36$ dır.
n hane ilerideki bir pulu kırma olasılığı. Eğer $n= 13$ ise, bu olasılık sıfırdır elbet. Ama $n= 15$ ise, pulu $(5, 5)$ zarıyla kırabiliriz, ve olasılığı $1/36$’dır. Bu olasılıkları bir dizelgeye sokalım
| n= uzaklık | Kırma olasılığı |
| 1 | $11/36$ |
| 2 | $11/36+1/36= 12/36$ |
| 3 | $11/36+1/36+2/36= 14/36$ |
| 4 | $11/36+1/36+2/36+1/36=15/36$ |
| 5 | $11/36+2/36+2/36=15/36$ |
| 6 | $11/36+2/36+2/36+1/36+1/36=17/36$ |
| 7 | $2/36+2/36+2/36=6/36$ |
| 8 | $6/36$ |
| 9 | $5/36$ |
| 10 | $3/36$ |
| 11 | $2/36$ |
| 12 | $3/36$ |
| 15 | $1/36$ |
| 16 | $1/36$ |
| 18 | $1/36$ |
| 20 | $1/36$ |
| 24 | $1/36$ |
Üç zara geçmeden önce, tavlanın sınırlı bir oyun olduğunu belirteyim. Yazdıklarımdan, tavlanın yüksek düzeyde bir bilim bilgisi gerektirdiği anlamı çıkmasın. Yani, tavlacı olmanızı salık vermem. Ama illâ tavlacı olacağını diyorsanız kesinlikle olasılık hesaplarını öğrenmeniz gerekir.
Şimdi üç zar alalım elimize ve yine ilk önce zarları birbirinden ayırdedelim: birinci zar, ikinci zar ve üçüncü zar. $6^3=216$ olay var, ve her olayın gerçekleşme olasılığı aynı olduğundan, her zarın gelme olasılığı $1/216$’dır. Örneğin,
$o(1-2-5)= o(1-5-2)= o(2-1-5)= o(2-5-1)= o(5-1-2)= o(5-2-1)= 1/216$ dır.
Ancak, zarları birbirinden ayırdetmemek en doğal olanı ve biz de etmeyelim. Olay sayımız azaldı, çünkü şimdi, örneğin $1-2-5$ve $5-1-2$ olayları arasında bir ayrım yapmıyoruz. Bu zara $(1, 2, 5)$ adını verelim. Kolayca görüleceği gibi
$o(1, 2, 5)= o(1-2-5) + o(1-5-2) + o(2-1-5) + o(2-5-1) +o(5-1-2) + o(5-2-1)= 6/216= 1/36$ dır. Bunun gibi, $o(3, 4, 6)$ da $1/36$’ya eşittir. Ama
$o(2, 2, 5)= o(2-2-5) + o(2-5-2) + o(5-2-2)= 3/216 = 1/72$,
ve
$o(2, 2,2)= 0(2-2-2)= 1/216$ dır.
Alıştırma olarak, üç zarla toplam $10$ atma olasılığını hesaplayalım:
$o(1, 3, 6) + o(1, 4, 5) + o(2, 2, 6) + o(2, 3, 5) + o(2, 4, 4) + o(3, 3, 4)=27/216 0,13 $
Yukarıdaki örneklerde olanak sayısı sonluydu. Örneğin, iki zarla $21$ olanak vardı. Şimdi, olanak sayımızı sonsuz yapacağız.
Kolay bir soruyla başlayalım: $[0, 1]$ aralığında rasgele seçilen bir (gerçel) sayının, $1/2$’den büyük olma olasılığı kaçtır? Yarısı $1/2$’dir. Çünkü, $[0,1]$ deki sayıların “yansı” $1/2$’den büyük, öbür “yansı” ise $1/2$’den küçüktür.
Bir kolay soru daha: $[0, 1]$ aralığında seçilen bir sayının $1/6$ ve $3/7$ arasında olma (olayının gerçekleşme) olasılığı kaçtır? Yanıt $3/7 — 1/6 = 11/42$’dir.
Buraya dek şaşılacak birşey yok.
Peki, $[0, 1]$ aralığında seçilen bir sayının $1/2$’ye eşit olma olasılığı kaçtır? Sıfırdır! Önsezi zorlanıyor biraz burada. Çünkü $1/2$ sayısı var, ve bana, “Bal gibi $1/2$’yi seçebilirim” diyebilirsiniz. ben de size, “madem öyle, bahse girelim” diyebilirim. bahse girmek istemezsiniz elbet. Çünkü kazanma olasılığınız sıfırdır! Olay sayısı sonsuzsa, ve her olayın gerçekleşme olasılığı aynıysa, o zaman, bir olayın gerçekleşme olasılığı sıfırdır. Şöyle açıklanabilir bu: diyelim $1/2$’yi seçme olasılığı $0,0001$. O zaman, herhangi bir sayıyı seçme olasılığı da, $0,0001$’dir, ve dolayısıyla aşağıdaki
$1/10.000, 2/10.000, 3/10.000, …, 10.000/10.000$
onbin sayıdan birini seçme olasılığını bulmak için $0,0001$’i onbin kez toplarız, ve $1$ buluruz, yani $%100$ olasılık! Olacak şey değil! Demek ki $1/2$ sayısını seçme olasılığı sıfır olmalıdır.
Şimdi iki sayı seçeceğiz ve sırayla seçeceğiz bu sayıları. Yani birinci sayıyla ikinci sayı arasında ayrım yapacağız. Soru şu: $[0, 1]$ aralığında rasgele ve sırayla iki sayı seçersek, ikinci sayının, birinci sayıdan büyük olma olasılığı kaçtır? Birinci sayıya $x$ adını verelim, ikinci sayıya $y$. Rasgele (ama sırayla) iki sayı seçmek demek, $[0, 1]$ X $[0, 1]$ karesinde rasgele bir $(x, y)$ noktası seçmek demektir.
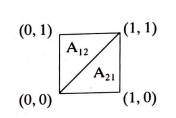
Yukarıdaki resimde $[0, 1]^2$ = $[0, 1]$ X $[0, 1]$ karesi üç değişik olay bölgesine ayrılmış:
$A_{12} = {{(x, y) \in [0, 1]^2 : x < y}}$
$A_{21} = {(x, y) \in [0, 1]^2 : x > y}$
ve ortadaki çizgi $A_{x=y} = {(x, x) \in [0, 1]^2 : x \in [0, 1]}.$
Resimden de görüldüğü üzere, bir $[0, 1]^2$ karesindeki rasgele bir $(x, y)$ noktasının, $A_{12}$ Bölgesinde olma olasılığı $1/2$’dir. $A_{21}$ bölgesinde olma olasılığı da $1/2$’dir. $A_{x=y}$ bölgesinde olma olasılığı ise sıfırdır.
Daha da zor bir soru soralım. Üç sayı seçelim, $[0, 1]$ aralığından: $x, y, z$. $x$ birinci sayı, $y$ ikinci ve $z$ üçüncü. $x < y < z$ olayının gerçekleşme olasılığı kaçtır? Bu üç sayıyı, $[0, 1]^3$ kübünde bir nokta olarak görebiliriz. Yukarıdaki gibi bir resim çizmeye çalışabilirsiniz. Ben denedim beceremedim. Üç boyutta görebilmek kolay değil. Ama şöyle akıl yürütebiliriz: $[0, 1]^3$ kübünü, şu bölgelere ayıralım:
$A_{123} = \{(x, y, z) : x < y < z\}$
$A_{132} = \{(x, y, z) : x < z < y\}$
$A_{213} = \{(x, y, z) : y < x < z\}$
$A_{231} = \{(x, y, z) : y < z < x\}$
$A_{312} = \{(x, y, z) : z < x < y\}$
$A_{321} = \{(x, y, z) : z < y < x\}$
Birinci bölgenin oylumunu (hacmini) bulmak istiyoruz. Bu altı bölgenin oylumları birbirine eşittir (hiç birinin oylumunun öbüründen büyük olması için bir neden yok). $[0, 1]^3$ kübünden geriye kalan bölgeler, yukarıdaki bölgelerin “duvarlarıdır” ve oylumları yoktur. Demek ki, bu altı bölgenin oylumlarının toplamı, $[0, 1]^3$ küpünün oylumuna, yani bir bire eşittir. Ve bundan da, her bir bölgenin oylumunun $1/6$ olduğu çıkar. Ne bulduk? $[0, 1]$ aralığından rasgele üç sayı seçersek, ikinci sayının birinci sayıdan ve üçüncü sayının ikinci sayıdan büyük olma olayının gerçekleşme olasılığının $1/6$ olduğunu bulduk.
Şimdi dört sayı seçeceğiz $[0, 1]$ aralığından ve ikinci sayının birinci sayıdan, üçüncü sayının, ikinci sayıdan ve dördüncü sayının üçüncü sayıdan büyük olma olayının gerçekleşme olasılığını hesaplayacağız. Dört boyutta olduğumuzdan resim çizemeyiz artık. Ama yine de yukarıdaki gibi düşünebiliriz.
$A_{1234}= \{(x_1, x_2, x_3, x_4) \in [0, 1]^4 : x_1 < x_2 < x_3 < x_4\}$
kümesi olsun. Bunun gibi örneğin,
$A_{3142}= \{(x_1, x_2, x_3, x_4) \in [0, 1]^4 :x_3 < x_1 < x_4 < x_2\}$
kümesini tanımlayalım. Tüm bu kümelerin “oylumları” aynı (dört boyutta oylum entegral hesaplarıyla bulunur, ama şu anda önsezi yeterli). Kaç tane bu tür küme var? Teker teker sıralayıp 24 tane olduğunu bulabiliriz kolaylıkla: $A_{1234}, A_{1243}, A_{1324}, A_{1342}$, … Geriye kalan kümeler, bu kümelerin “duvarları” olduklarından oylumları sıfırdır. Demek ki, bulmak istediğimiz olasılık $1/24$’dür.
Şimdi çok genel bir soru soralım: $[0, 1]$ aralığından $n$ tane rasgele ve sırayla sayı seçiyoruz: $x_1, x_2, …, x_n$. Bu dizinin artan bir dizi olma olasılığı kaçtır? Yani $x_1 < x_2 < … < x_n$ olayının olasılığı kaçtır? Yukarıdaki gibi akıl yürüteceğiz.
$A_{1,2,…,n}=\{(x_1, x_2, …, x_n) \in [0, 1]^n :x_1 < x_2 < … < x_n\}$
kümesinin oylumunu arıyoruz. Bu tür kümelerden kaç tane olduğunu bulmalıyız. Yani, $1, 2, …, n$ sayılarını kaç türlü dizebiliriz? $n!=$ $1$ X $2$ X … X $(n – 1)$ X $n$ türlü dizebiliriz diyorum. Bunu tümevarımla kanıtlayacağım. İlk önce, ilk $n-1$ sayıyı $(n-1)!$ türlü dizebildiğimizi varsayalım. Bu dizilerden herhangi birini alalım. Şimdi, son sayıyı, yani n sayısını, araya bir yere sokacağız. Başa, ortaya ya da en sona sokabiliriz: toplam n değişik yere sokabiliriz. Demek ki $1, 2, …, n$ sayılarını $(n-1)!$ X $n$=$n$! türlü dizebiliriz. Dediğimi kanıtladım. Bundan da şu sonuç çıkar: Rasgele $0, 1$ aralığında seçilen $x_1, …, x_n$ dizisinin artan bir dizi olma olasılığı $1/n!$‘dir.
Örneğin $n=2, 3, 4$ ise yukarıda bulduğumuz $1/2, 1/6, 1/24$ olasılıklarını buluruz. Dikkat ederseniz, $n$ büyüdükçe olasılık azalıyor. Örneğin, $n=5$ için, $1/5! = 1/120 = 0,00833…$ olasılığını buluruz. $n=6$ için ise, $1/6!=1/720=0,0014$ olasılığını.
Şimdi yazının en son sorusuna geldik: $[0, 1]$ aralığında rasgele seçilen sonsuz bir sayılar dizisinin artan bir dizi olma olayının gerçekleşme olasılığı kaçtır? Yanıt kolay: $\lim_{x \to \infty}1/n!=0.$
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

