Yazar: Azize Bastıyalı Hayfavi
Sayı: 1992-4
Düzgün çokgen, tüm kenar uzunlukları eşit ve tüm iç açıları aynı olan çokgenlerdir
n-kenarlı bir düzgün çokgen çember içine çizildiği zaman, merkezden iki komşu köşeye çizilen yarıçapların oluşturduğu merkezi açı
$ (\frac{360}{n})^\circ $ veya $ \frac{2\pi}{n} $ radyandır.
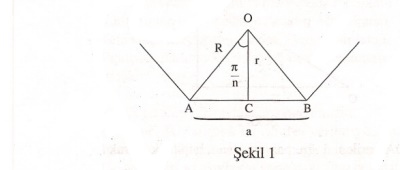
Şekil 1 Şekil 1’de görüldüğü gibi, n- kenarlı bir düzgün çokgenin kenar uzunluğunu, $|AB|= a $ , iç çember yarıçapını $|OC|= r$, çevrel çemberin yarıçapını $|OA|=R$, ve alanını da $S$ ile gösterelim. Çokgenimiz n-kenarlı olduğundan $\widehat{AOB}$ açısı $\frac{2\pi}{n}$ radian ve bunun yarısı olan $\widehat{AOC}$ açısı $\frac{\pi}{n}$ radiandır. Böylece AOC dik üçgenini dikkate alarak hemen:
$\frac{a}{2} = R \sin{\frac{\pi}{n} }$ ve $\frac{a}{2} = r \tan{\frac{\pi}{n} }$
eşitliklerini yazabiliriz.
Bu eşitliklerden birisini $R$’ye, ikincisini de $r$’ye göre çözerek
$R= \frac{a}{ 2\sin{\frac{\pi}{n} } }$ = $\frac{a}{2}\csc\frac{\pi}{n}$ ve
$r= \frac{a}{ 2\tan{\frac{\pi}{n} } }$ = $\frac{a}{2}\cot\frac{\pi}{n}$
elde edilir.
n
Tekrar Şekil I ‘e bakarak n—kenarlı bir çokgenin alanı için de:
$S= n $[AOB üçgenin alanı]$ =$ $ n \frac{1}{2}|AB| \cdot |OC|$ = $n|AC||OC|$
olduğu görülür
Böylece,
(i) kenar uzunluğu cinsinden :
$S= n\frac{a}{2}r=n\frac{a^2}{4}\cot{\frac{\pi}{n}}$
olarak
(ii)R cinsinden :
$S= n R \sin{\frac{\pi}{n}} R \cos{\frac{\pi}{n}} =n\frac{R^2}{2}\sin{\frac{2\pi}{n}}$
olarak
(iii)r cinsinden :
$S=n r (\tan\frac{\pi}{n}) r = nr^2 \tan\frac{\pi}{n} $
olarak ifade edilebilir.
Örneğin, bir düzgün üçgen için, yani bir eşkenar üçgen için yukardaki formülleri kullanarak;
$a=R\sqrt{3}$, $r=\frac{R}{2}$, $R=\frac{a\sqrt{3}}{3}$, $r= \frac{a\sqrt{3}}{6} $, $S= \frac{a^2\sqrt{3}}{4} $, $S= \frac{3R^2\sqrt{3}}{4} $
formüllerini hemen yazabiliriz.
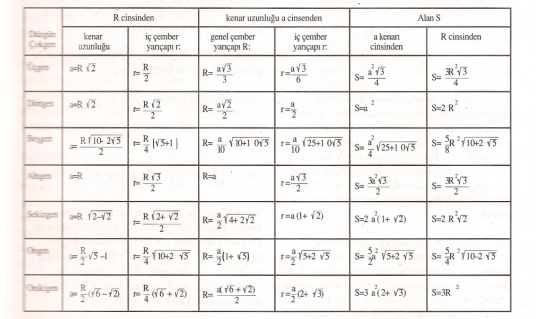
Çokgenlerle ilgili diğer bağıntıları, yazının sonundaki Tablo’da bulabilirsiniz.
Şimdi de hangi düzgün çokgenlerin çizilebilir olduklarını ve nasıl çizilebileceklerine bakalım.
Bazı düzgün çokgenlerin çizimi ta Pythagoras (M.Ö. 530) zamanından beri bilinmektedir.
Bunlar, kenar sayıları 3,4,5,6,8,10 veya bu sayıların iki katı olan düzgün çokgenlerdir. Fakat düzgün 7 genin pergel-cetvelle çizilemediğini de fark ettiler. Böylece hangi düzgün çokgenlerin Euclid anlamında (yani pergel ve cetvel kullanarak) çizilebilir oldukları konusu gündeme gelmiştir.
Bu soruya yanıt ancak Gauss (1777-1855) tarafından verilebilmiştir. Bunun için evvela Fermat sayılarına tanımlıyalım. $2^{2^n}+1$ şeklindeki sayılar Fermat sayıları olarak bilinmektedir ve Fermat tüm bu sayıların asal sayılar olduklarına İnanmaktaydı. Hakikaten
$ n =0$ için $2^{2^0}+1=3$ , $ n =1$ için $2^{2^1}+1=5$, $ n =2$ için $2^{2^2}+1=17$, $ n =3$ için $2^{2^8}+1=257$, $ n =4$ için $2^{2^4}+1=65537$ sayıları asal sayılardır.
Fakat $ n =5$ için $2^{2^5}+1$ sayısının asal olmadığı Fermat’dan bir yüzyıl sonra Euler tarafından ispatlanmıştır. Ayrıca, şimdiye kadar $n =6,,7,8,9$ için de Fermat sayılarının asal olmadıkları İspatlanmıştır. Fakat hala Fermat asal sayılarının sonlu sayıda olup olmadığı sorusu yanıtlanamamıştır.
Fermat sayılarını tanımladıktan sonra tekrar konumuza dönelim. Gauss evvela $17$ kenarlı düzgün çokgenin Euclid anlamında çizilebilir olduğunu gösteriyor ve daha sonra da kenar sayıları diğer Fermat asal sayılarına eşit olan düzgün çokgenlerin çizilebildiklerini ispatlıyor. Bununla da kalmayıp, m pozitif bir tam sayı ve $P_1,P_2,…,P_r$ farklı Fermat asal sayıları olmak üzere, tüm$ N=2^m P_1,P_2,…,P_r $ kenarlı düzgün çokgenlerin de çizilebilir olduklarını ispatlamıştır. Böylece, şimdiye kadar kenar sayısı asal olan yalnızca 5 tane düzgün çokgen çizilebilmektedir. İki tanesi M.Ö. 530’lardan beri bilinmektedir (düzgün üçgen ve düzgün beşgen) üç tanesi de Gauss tarafından keşfedilmiştir. Bunlar kenar sayıları $17, 257$ ve $65537$ olan düzgün çokgenlerdir.
Biz bunlardan sadece düzgün beşgenin çizimini vermeye çalışacağız. Bunun için evvela düzgün on kenarlıyı çizeceğiz ve köşelerini birer atlayarak birleştirerek düzgün beşgenimizi elde edeceğiz.
Verilen $R$ yarıçaplı bir çember içine düzgün ongen çizmek için $R$ uzunluğunu “altın oran”* olarak bilinen oranda bölmek gerekiyor. Bunun için evvela verilen bir doğru parçasını geometrik yoldan altın oranda nasıl böleceğimizi görelim.
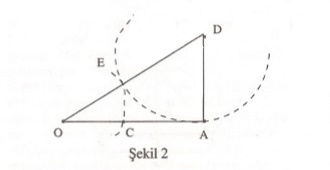
$OA$ verilen doğru parçası olsun, buna dik olarak $AD=\frac{1}{2} OA$ doğru parçasını çizelim (Şekil 2).
Eğer $|OA|=R$ ise $|AD|=\frac{R}{2}$ olur. Daha
sonra $O$ ile $D$ yi birleştirdiğimizde, hipotenüs
uzunluğu $|OD|= \frac{\sqrt{5}}{2}R$ olan $OAD$ dik ongenini elde ederiz. Şimdi $D$ köşesini merkez olarak alıp, yarıçapı $|DA|$ olan daire yayını çizelim. Bu daire yayı $DO$ kenarını $E$ noktasında kessin.
Böylece $|OE|= \frac{\sqrt{5}}{2}R-\frac{R}{2}= \frac{\sqrt{5}-1}{2} R$ = $(0.618 …)R$ olur.
* OA doğru parçasını altın oranda bölmek demek, O ve A arasında öyle bir C noktası bulmak demektir ki OA : OC=OC : CA olsun.Daha sonra $OE$ yi pergelle $OA$ üzerine taşıdığımızda, $AO$ nin altın bölümünü veren $C$ noktasını bulmuş oluruz. Gerçekten :
$|OA| : |OC|=|OC| : |CA|$ olduğunu hemen gösterebiliriz. Hakikaten :
$R= \frac{\sqrt{5}-1}{2} R $=$ \frac{\sqrt{5}-1}{2} R : (R- \frac{\sqrt{5}-1}{2} R )$
dir
Altın oran, bir takım geometrik çizimlerin gerçekleştirilmesinde kullanılmasının yanı sıra, doğada, mimari yapılarda da hep karşımıza çıkmaktadır. Örneğin, Atinada bulunan Akropolİs’dekİ Parthenon mabedinde bu oranın kullanımına bolca rastlanmaktadır. Altın oranın hem sıkça karşılaşılmasından, hem de bir takım ilginç özelliklerinden dolayı ayrıca ele alınması gerekir.
Şimdi gelelim bizim düzgün ongenimizin çizimine, $R$ yarıçaplı bir çember verilmiş olsun, bunun içine düzgün ongen çizmeye çalışacağız. Göstereceğiz ki çemberin yarıçapını altın oranda böldüğümüz zaman büyük olan kısmı bu çemberin içine çizilen düzgün ongenin kenar uzunluğuna eşittir
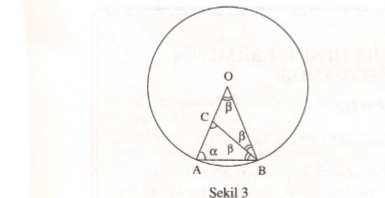
Şekil 3’de görüldüğü gibi çemberin yarıçapı $|OA|= R$ uzunluğunda olsun ve $C$ noktası $OA$ yi altın oranda bölen nokta olsun, yani
$|OA| : |OC|=|OC| : |CA|$
olsun. Göstereceğiz ki $|OC|$] bu çemberin içine
çizeceğimiz düzgün ongenin kenar uzunluğudur.
Şekil 3’de görüldüğü gibi A noktasından başlayarak kenar uzunluğu $|OC|$ olan düzgün çokgeni çizmeye başlarsak tam bir düzgün ongen elde ederiz. $|AB|$ = $|OC|$ dir. Bunun düzgün ongen olduğunu göstermek için $OAB$ İkizkenar üçgeninde tepe açısının $36^{\circ}$ olduğunu göstermek yeterli olacaktır.
$OAB$ ikizkenar üçgeninde, taban açılarını $\alpha$ ile gösterelim $CD$ yi birleştirelim.
Altın bölmeden dolayı :$\frac{OA}{OC}= \frac{OC}{CA} $ dır
Fakat $OA=OB $ ve $OC=AB$ olduğundan aynın oranı
(**) $\frac{OB}{BA}= \frac{BA}{CA}$
yazabiliriz.
Şimdi $OAB$ ve $CAB$ üçgenlerini dikkate alalım. Bunlar bir açılarının ortak olmasından ve (**) daki oranların eşitliğinden dolayı, benzer üçgenlerdir. Öyleyse $\widehat{AOB}$ = $\widehat{CBA}$ dır. Şekilde bunları $\beta$ İle gösterdik. Benzerlikten dolayı $CAB$ de ikizkenar üçgendir, yani $CB=AB$ dir. Demekki $OC=AB=CB $ dir.
Böylece $OCB$ ninde ikizkenar üçgen olduğu görülür. Öyleyse taban açıları :
$ \widehat{OBC}= \widehat{AOB}=\beta $ dır.
Bir üçgende İç açılar toplamı $180^{\circ}$ olduğundan
$180^{\circ}= \widehat{BOA} + \widehat{OBA} + \widehat{BAO} =\beta + \alpha + \alpha$
Fakat $\alpha=2\beta$ olduğundan
$180^{\circ}= \beta + 2\beta + 2\beta$
$180^{\circ} = 5\beta$ , $\beta=(\frac{ 180^{\circ} }{5})= 36^{\circ}$
olduğu görülür.
$AB$ kirişini gören merkezi açı $36^{\circ}$ olduğundan, $AB$ kirişi, $R$ yarıçaplı çemberin içine çizilen düzgün ongenin kenarıdır. Düzgün ongeni elde ettikten sonra köşelerini bir atlayarak birleştirirsek düzgün beşgen elde edilmiş olur. Düzgün $17$ kenarlının çizimini Howard EVS’in “A survey of Geometry” Vol.1 kitabında bulabilirsiniz.
düzgün çokgenlerde kenar uzunluğu, iç ve dış çember yarıçapları ve alanları ile ilgili bağıntılar
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 4. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

