Yazar: Stanislaw Lem
Yıl: 1992-5
Sayı: 10
Eve oldukça geç döndüm. Andromedalılar kulübündeki toplantı gece yarısından çok sonraya dek uzamıştı. Bütün gece kabus gördüm: önceleri dev yaratıklarla uğraştım. Sonra da kendimi yeniden Durtitov gezegeninde buldum. Üstelik, o korkunç makinadan, hani o insanı altıgene çeviren ve asla eski haline dönüştüremeyen makinadan nasıl korunacağımı bilemiyordum. Neyse ki hesapta olmayan bir telefonla uyanarak kabuslarımdan sıyrıldım. Hattın öbür ucunda eski dostum ve yıldızlar arası seyahat arkadaşım profesör Tarantog vardı. Sesinden, gene üstesinden gelemediği bir işle karşılaştığı belliydi:
“-Dostum Mülayim, ilginç bir problemle karşı karşıyayız. Astronomlar bir galaksi boyunca uzanan kara bir bant keşfettiler. Ne olduğunu kimse bilemiyor. En iyi teleskopları ve radyo teleskopları takıp gönderdiğiniz roketler bile bu esrarengiz nesneyi anlayamadan döndüler. Saatlerdir bu işle uğraşıyoruz. artık başka yollardan umudu kestik; seni oraya gönderip olayı yerinde görmen gerektiğine karar verdik. Hemen ACD-1587 takım yıldızına doğru yola çıkmaya hazırlan… ”
Ertesi gün emektar foton roketimi tamirciden çektim. Yolculuk için gerekli her şeyi içine yerleştirdim. Özellikle, yıldızlar arası bütün dilleri ve en güzel öyküleri bilen elektronik robotumu göğüs cebime yerleştirmeyi unutmamaya dikkat ettim. Gideceğim yerde, onsuz hiç kimseyle konuşamayacağım gibi, bu uzun yolculukta her an gönlümün dilediği türden öyküler anlatmasa, can sıkıntısından ölebilirim. Robotum en az beş yıllık bir yolculuğa yetecek kadar öykü bilmektedir.
Yola çıktım.
Her zaman olduğu gibi, önceleri yolculuğum çok iyi geçiyordu. Hatta, dostum Tarantog’un verdiği bu işten memnun bile olmuştum. Ama roketimin zaman ayarındaki bir bozukluk nedeniyle, yolculuk umduğumdan daha çok sürdü. Dönüşte, ya tamircimi değiştireceğim ya da roketimi. Zavallı robotum, ben sıkılmayayım diye en az on kez devrettiği öyküler arasından, o an için hoşlanabileceğimi sandıklarını bir daha seçmeye uğraşıyordu. (Bir elektronik robottan bir öyküyü on kez dinlemekten daha berbat bir şey olamayacağını ona ne diye öğretmemişler sanki!) Neyse ki sonunda hedefimiz uzaktan göründü. Galaksiye yaklaştıkça, ne olduğunu dünyadan anlayamadığımız o kara bantın, hemen hemen her burçta kumlan heyula birer yapı olduğunu gördüm. Uzaktan bakınca biz, bu yapılan galaksiyi boydan boya aşan kara bir bant olarak gömüştük.
Bu yapılardan çoğunu geride bırakarak galaksinin merkezine ilerledim ve bu heyula yapılardan biri olan Kozmoz oteline indim.
Bir zamanlar bu galakside görevliydim. O zamanlar gezginlerin sığınacağı küçük peykler yaptırmıştık. Ancak, zamanla gezginlerin sayısı çok arttığından, galakside peyk trafiği tehlikeli bir hal almış. Üstelik gelişen evrende bu peykler oldukça ilkel görülmeye başlanmış. Bunun üzerine, peykleri toplayıp onların yerine, hemen hemen her bir burçta sonsuz odalı birer otel yapmaya karar vermişler. Hemen her burçta diyorum, çünkü inşaat sırasında, galaksideki canlıları bir araya topladıkları birkaç milyon burç hariç, ötekilerin (ki sonsuz sayıdadır) her birisine bir otel kurmuşlar. Böylece sonsuz odalı bu oteller, hem bulundukları burcun bölgesindeki bütün yıldızlara hem de başka galaksilerden o yıldızlara gelecek gezginlere yetsin diye düşünülmüş. Yapım sırasında, galaksiye ait öteki yıldızlardan büyük miktarlarda yapı malzemesi taşınmış.
Gerçekten oteller birer harika!.. Sonsuz odalı Kozmoz otelinin her bir odasında, herhangi bir galaksiden gelecek müşterinin yaşam koşullarına ayarlanabilecek her türlü konfor var. Odayı istediğiniz gazla doldurabilir, istediğiniz sıcaklığa ayarlayabilirsiniz. Musluklardan isterseniz sıcak ya da soğuk su, isterseniz istediğiniz kıvamda plazma akar. Dilerseniz, gece sizi atomlarınıza ayırırlar, sabahleyin yeniden birleştirirler. Doğrusu bu galakside uygarlık bizimkinden daha ileride. Bizimkilerin, bu gidişle, kalkınma hızını yeniden ayarlamaları gerekecek.
Bütün bunlara karşın otele indiğimde pek talihli sayılmazdım. Otel yeni açılmıştı. Personel henüz işlere iyice alışamamıştı. Üstelik uzay zoologları kongresi burada toplanmıştı. Öteki bütün galaksilerden gelen zoologlar otele benden daha önce inmişlerdi. Sonsuz çokluktaki bu galaksilerden gelen bu müşteriler, sonsuz odalı Kozmoz otelini çoktan doldurmuşlardı bile.
Roketim bakım görmeden ve ben de iyice dinlenmeden ne dünyaya dönebilirdim, ne de bir başka burçta boş otel aramak için yola çıkabilirdim. Otel katibi halden anladı, Önce, telefonla odaları yoklayarak, odasını benimle paylaşacak bir zoolog aradı. Sonunda da, iki gönüllü centilmen buldu. Ne yazık ki bu centilmenlerden birisi odasını flüor gazı ile doldurmuştu, ötekinin de 8600 C de uyuması gerekiyordu. Nazik kabulleri için her ikisine de ayrı ayrı teşekkür ederek, yine katibin yanına döndüm. Katip bu kez otel müdürüne çıktı. Adımı duyan müdür koşarak yanıma geldi. Mutlu bir tesadüf, kendisi buradaki eski dostlarımdan birisiydi. Hemen katibe emretti:
“-Konuğunuzu $1$ numaralı odaya al.”
Katip biraz şaşkın cevap verdi:
“-Peki ama $1$ numaralı odadaki müşteriyi ne yapayım?”
“- $1$’dekini $2$’ye, $2$’dekini $3$’e, $3$’tekini $4$’e al. Böylece bütün müşterileri birer numara geriye kaydır. ”
Bu cevaptan sonra, otelin olağanüstü bir özelliğini anlamıştım. Eğer sonlu sayıda oda olsa idi, her müşteri bir geriye kayınca, en son odadaki müşteriye yer kalmazdı. Ama oda sayısı sonsuz olduğu için, hiçbir müşteriyi otelden çıkarmadan, herkesi birer birer geriye kaydırmak mümkündü.
Ertesi gün $1000000$ numaralı odaya geçmem rica edilince hiç şaşırmadım. Zira VSK-3472 numaralı galaksiden gelen zoologlar benden sonra yetişmişlerdi, dolayısıyla, otel müdürü bu gruba dahil $999 999$ yeni müşteriye yer açıyordu.
Ertesi gün hesabı ödemek üzere aşağıya indiğimde, katibi çok telaşlı gördüm. Holdeki kayıt bürosunun önünde kuyruğa girmiş olan bir kalabalıktan gürültüler geliyordu:
“-Andromedadan iki pullun var. Sirius’dan iki pul ile değiştirmek istiyorum. . .“
“-Erpean’dan 57. uzay yılına ait bir pul arıyorum. . .“
Katibe,
“-Bunlar da kim ?“
diye sordum.
“-Yıldızlar arası pulcular kongresinin delegeleridir. “
diye cevap verdi.
“Çok mu kalabalıklar ?
“-Hem de nasıl. . . Sonsuz çoklukta. . . Herbir galaksiden bir delege var. “
O an pencereden dışarıya baktım. Holdeki kuyruk, dışarıda taa Macellan bulutuna doğru uzayıp gidiyordu.
“-Peki ama bunlara nasıl yer bulacaksınız şimdi! Üstelik zoologlar yarına kadar otelden ayrılmayacaklar…“
dedim.
“-Doğrusu ben de bilmiyorum. Zaten şimdi durumu müdüre anlatmaya gidiyordum. Lütfen beni birkaç dakika bekleyiniz.”
diyerek katip odadan çıktı.
Görünüşe bakılırsa bu kez problem daha zor çözülmüştü. Katibin birkaç dakikası bir saati çoktan aşmıştı ki, yorgun ama memnun bir yüzle odasına döndü. Benim varlığımı bile unutarak, adamlarına buyruk vermeye başladı:
“- $1$ numaradakini $2$ numaraya…”
diye söze başladı. Ben o an neredeyse içimden kıs kıs gülmeye başlayacaktım. Çünkü bu yöntemi benim için uygulamışlardı ve biliyordum ki bu iş ancak sonlu sayıda müşteriye yer açabiliyordu. Oysa bunların kapısında sonsuz çoklukta müşteri kuyrukta bekliyordu. Ama katip sözünü,
“- $2$ numaradakini $4$ numaraya, $3$ numaradakini $6$ numaraya; genel olarak $n$ numaradakini $2n$ numaraya yerleştiriniz.”
diye bitirince, sorunu gerçekten çözdüklerini anladım. Bu yöntemle sonsuz çoklukta olan tek numaralı odaları boşaltabiliyordu.
Artık bunlara pulcuları yerleştirebileceklerdi. Böylece çift numaralı odalar da uzay pulcuları tarafından işgal edilmiş olacaktı.
Roketimin bakım yapılmış, geri dönüş için her şey hazır olmuştu. Ama dönüş zamanımı biraz daha ertelemeye karar verdim. Erteleme kararımın nedeni, ne Kozmoz otelinin konforu ve ne de uzay zoologları ile kurduğum içten dostluklar idi. Bütün bunlardan daha çok, bu otelin, karşılaştığım bu olağanüstü özellikleri, beni dönüş kararımdan vazgeçirdi. Biraz daha kalırsam, belki Kozmoz otelinin başka olağanüstü özelliklerini daha öğrenebilirdim. Gecikeceğim için dostum Tarantog’un canı sıkılsa bile, bu merakımı yenemeyecektim. Sonunda, ben de, bütün zoologlar gibi, odamı değiştirdim ve $1 000 000$ numaralı odadan çıkıp $1 999 999$ numaralı odaya yerleştim. Bu arada Samanyolu galaksisinden gelen ve kuyrukta $574$ ‘üncü sırada yer alan pulcu bir arkadaşım $1147$ numaralı odaya yerleşmişti. Genel bir kural diye söylersek, pulcuların meydana getirdiği kuyrukta $n$’inci sırada yer alan bir müşteri $2n-1$ numaralı odaya yerleşmişti.
Ertesi gün zoologların kongresi bitip her biri kendi yurduna dönünce otelde bir ferahlama sezildi. Bu arada otel müdürü arkadaşım, beni, kendisine ayrılan lojmandaki boş bir odaya yerleştirmek nezaketinde bulundu. Otelin yarısı boşaldığı için müşteriler kadar otel personeli de memnun görünüyordu. Ama onları memnun eden bu olgunun, otel müdürünü memnun etmediği anlaşılıyordu.
“-Otelin yarısı boşaldı. Bu gidişle işletmemiz zarara girecek!..”
diye dertlendi. Gerçekte, sonsuz müşterisi olan bir otelin nasıl olup ta zarar edebileceğini anlayamadım. Ama konuşmuş olmak için,
“-Öyleyse müşterilerini tekrar sıklaştır; zoologlarda olduğu gibi otel yeniden dolsun.“
dedim.
“-Hay Allah!.. bunu neden düşünemedim şimdiye dek!”
diye hayıflandı. Hemen telefona sarılarak katibe ne yapacağım anlattı. Zaten bu kez problem kolaydı. Pulcular $1, 3, 5, 7…, 2n-1,…$ gibi tek numaralı odaları doldurmuşlardı. Öyleyse, $1$ numaradakini yerinde bırakarak, $3$ numaradakini $2$ numaraya, $5$ numaradakini $3$ numaraya; genel olarak, $2n-1$ numaradakini $n$ numaraya yerleştirmek yetecekti. Böylece, yarısı boş olan otele hiçbir yeni müşteri gelmediği halde, mevcut müşterilerle otel yeniden doldurulmuştu.
Yazık ki bu sorunun çözümüyle müdürün sevinci uzun sürmedi. Galakside hemen her burçta kurulan herbiri sonsuz odalı sonsuz çokluktaki otellerin hemen boşaltılması buyruğu gelmişti. Otellerin inşaatı sırasında öteki yıldızlardan taşınan yapı malzemeleri nedeniyle galaksi içi yıldızlar arası çekim dengesinin bozulduğu saptanmıştı. Bunun ileride ciddi sorunlar yaratmasından korkuluyordu. Bu nedenle, bu otellerin yıkılıp, herbir yıldıza ait malzemelerin geriye götürülmesi kararlaştırılmıştı. Yıkım işine hemen başlanılacağından, bu otellerin bütün müşterilerinin beş gün içinde Kozmoz oteline yerleştirilmesi öngörülmüştü. Zavallı dostum, Kozmoz oteli müdürü, önüne gelene dert yanıyordu:
“-Önce, her odası dolu otelime yeni bir müşteri geldi. Yer yok demedim. Ona bir oda buldum. Sonra $999 999$ yeni müşteri daha geldi. Onları da geri çevirmedim. Her birine bir oda buldum. Daha sonra, tamamen dolu olan otelimin oda sayısı kadar yeni müşteri daha geldi. Onlara da yer yok demedim, her birisine bir oda verdim. Ama bu kez ne yapabilirim ben? Sonsuz çoklukta burç, her burçta bir otel, her otelde sonsuz çoklukta müşteri var. Şimdi bütün bunları, zaten tamamen dolu olan otelime nasıl yerleştiririm? Bu buyruğu verenler beni sihirbaz mı sanıyorlar?”
Müdürün bu şekilde yakınması birkaç saat sürdü. Ne var ki, buyruk buyruktu ve buyruğun yerine getirilmesi için zaman daralıyordu. Baktı ki yakınmanın yararı yok, oturup sorunu ciddi olarak düşündü. Çözüm bulamayınca, problemi bir yarışma ile çözmeye karar verdi. Otelin her yanına duyurular astırdı. Problemi açıkladı. Bu sorunu çözümleyene istediği bir galaksiye gezi yapma olanağı sağlayacaktı. Oteldeki bütün müşteriler ve bütün personel her işi bir yana bırakıp bu problemi düşünmeye başladılar.
Neden sonra aşçılardan birisi heyecanla müdürün odasına daldı ve şu öneride bulundu:
“-Birinci otel bizimki olsun. Bizim otelde, $1$ numaradaki müşteriyi yerinde bırakın. $2$ numaradakini $1001$ numaraya, $3$ numaradakini $2001$ numaraya, $4$ numaradakini $3001$ numaraya v. b. yerleştiriniz. Sonra ikinci oteldeki müşterileri, bizim otelin $2, 1002, 3002$ numaralı odalarına yerleştiriniz. Sonra üçüncü otelin müşterilerini bizim otelin $3, 1003, 2003, 3003, 4003, …$ numaralı odalarına yerleştiriniz. Artık, bu işe, böylece devanı ediniz. ”
Odadakiler bir an duraksadı. Acaba sorun çözümlenmiş miydi? Müdür, söylenenleri en başından dikkatle yeniden düşünmeye koyuldu. Biraz sonra aşçıya döndü ve şöyle dedi:
“-Bak, sana, bir eski hikaye anlatacağım. Eski Roma senatosu, imparator Tiberius’un onuruna, Eylül ayının adım “Tiberius” olarak değiştirmeyi önerir. (Temmuz=julius ve Ağustos=Augustus adları daha önce imparator adlarını almışlardı.) Tiberius, iğneli bir ifadeyle senatosuna şu cevabı verir: “-Peki ama onüçüncü Sezara ne önereceksiniz?” Şimdi ben de sana şunu soruyorum: Önerdiğin plana göre, öncelikle, bizim otelin bütün müşterilerini, değişik bir biçimde gene bizim otele yerleştiriyorsun. Sonra ikinci otelin bütün müşterilerini de aynı şekilde Kozmoz’a yerleştirebiliyorsun. Üçüncü, dördüncü, …, bininci otelin bütün müşterilerini de aynı plana göre yerleştirebileceğimden hiç kuşkum yok. Peki buna 1001 inci ve ondan sonraki otellerin müşterilerini ne yapacaksın?”
Aşçının planı ilginçti ama problemi tam çözemiyordu.
Biraz sonra otel muhasebecisi bir başka öneriyle çıkageldi. Bunun önerisi geometrik dizilere dayanıyordu. Birinci oteldekileri $2, 4, 8, 16, 32, …$ numaralı odalara; başka bir deyişle $2, 2^2, 2^3, 2^4, 2^5, …$ numaralı odalara yerleştirecekti. ikinci oteldekileri $3, 9, 27, 81$ numaralı odalara; başka bir deyişle, $3, 3^2,3^3, 3^4, …$ numaralı odalara yerleştirecekti. Üçüncü oteldekileri $4, 4^2, 4^3, …$ numaralı odalara, … Böylece devam ediyordu ki, müdür sözünü kesti:
“-Herkese bir oda istiyoruz. Bu plana göre, örneğin, birinci otelin $2$ numaralı müşterisi ile üçüncü otelin $1$ numaralı müşterisini Kozmoz’un $4$ numaralı odasına yerleştirmiş oluyorsunuz.”
Bir sessizlik çöktü odaya. Bu umut da mı boşa çıkıyordu? Bu noktada söze karıştım. Ne de olsa, Yıldız Akademisinde beş yıllık aritmetik öğretmenliğimin boşuna olmadığını ispatlamak fırsatı doğmuştu:
“-Baylar” dedim yalnız asal sayıları kullanırsak bu yöntem işler. Önce $2$ den başlayarak asal sayıları küçükten büyüğe doğru $2, 3, 5, 7, 11, …$ gibi sıralayalım. Birinci otelin müşterilerini ilk asal sayının kuvvetleri ile numaralanmış odalara; yani $2, 2^2,2^3, …$ numaralı odalara yerleştirelim. İkinci otelin müşterilerini ikinci asal sayının kuvvetleri ile numaralanmış odalara, yani $3, 3^2,3^3,… $ numaralı odalara yerleştirelim. Böylece devam edersek, üçüncü otelin müşterilerini $5, 5^2, 5^3,5^4 …$ numaralı odalara; dördüncü otelin müşterilerini $7,7^2, 7^3, …$ numaralı odalara v. b.”
Müdür:
–Yani, böyle yaparsak, bir odaya birden çok müşteri girme olasılığı kalkıyor mu?
diye sordu.
“-Elbette” diye cevap verdim “çünkü iki asal sayının pozitif tam kuvvetlerinden herhangi ikisi eşit olamaz; yani $p$ ile $q$ herhangi iki asal sayı ve $p \neq q$ ise, her $m, n$ pozitif tam sayıları için $p^m \neq q^n$dir. ”
Müdürün yüzü gülmüştü artık. Sorunun çözüldüğüne inanmıştı. Ancak işin pratik yönüne kolaylık kazandırmak için, son öneriyi şöyle değiştirdi:
-Yalnız $2$ ve $3$ asal sayılarını kullanalım. $n$’nci otelin $m$’inci odasından gelecek müşteriyi Kozmoz’un $2^m 3^n$ numaralı odasına yerleştirelim.
Gerçekten bu çok daha kolay uygulanabilir bir yöntemdi. Buna göre, herhangi numaralı bir otelin herhangi numaralı bir odasından gelecek müşteriye, Kozmoz’da hangi numaralı odaya yerleşeceğini, daha girişte kapıcı bile söyleyebilirdi. Tabii, $m\neq p$ ya da $n \neq q$ ise $2^m3^n \neq 2^p3^q$ olduğundan, her müşteriye bir tek oda verilecekti.
Artık, herkes memnundu. Çözülemez sanılan problem çözülmüştü! Ama ne ben, ne de müdür ortaya konan armağana hak kazanamıyorduk. Çünkü, bu çözüme göre otelin büyük bir kısmı boş kalıyor, dolayısıyla işletme zararı doğuyordu. Benim çözüme göre, örneğin, $6, 10, 12, …$ numaralı odalar, daha genel söylersek, bir asal sayının kuvveti olarak yazılamayan sayılara karşılık gelen bütün odalar boş kalıyordu. Müdürün çözümüne göre, $2^m3^n $ şeklinde yazılamayan sayılara karşılık gelen bütün odalar boş kalıyordu. Şu aksiliğe bakın ki, biraz önce, herbiri Kozmoz büyüklüğündeki sonsuz çokluktaki dolu otellerin müşterilerini, zaten dolu olan Kozmoz’a sığdıramıyorduk. Şimdi ise aynı müşterilerin hepsini Kozmoz’a yerleştirdiğimizde bile burayı dolduramıyoruz. Bu, Kozmoz’un karşılaştığım üçüncü olağanüstü özelliği oluyordu. Doğrusu geciktiğime değmişti.
Armağanı kazanan çözümü, bir pulcular delegesi olan Swan galaksisi Matematik Akademisi başkanı önerdi. Başkan, sıralı çiftlerden oluşan şöyle bir tablo düzenlemişti. Sıralı çiftlerden herbirisi bir müşteriyi gösteriyordu. Örneğin, $5$ inci otelin $102$ numaralı odasındaki müşteriyi $(5,102)$ sıralı çifti ile; daha genel söylersek, $m$-inci otelin $n$-inci odasındaki müşteriyi $(m,n)$ sıralı çifti ile temsil ediyordu. Sonra birinci otelin müşterilerini temsil eden sıralı çiftleri bir satır halinde yazıyor, o satırın altına ikinci otelin müşterilerini temsil eden sıralı çiftleri, onun altına üçüncü otelin müşterilerini , … v. b. böylece şöyle bir tablo ortaya çıkıyordu:

Artık, sözkonusu büyün müşteriler bu tabloda yer alıyordu. Örneğin, $7000$ inci otelin $888.888$ numaralı odasındaki müşteriyi temsil eden $(7000,888.888)$sıralı çifti. tabloda $7000$ inci satır $888.888$ inci sütunun kesiştiği yerde yer alıyordu.
Tabloyu hepimiz az çok anlamıştık, ama bu tablonun ne işe yaradığını anlayamıyorduk. Başkan kısa konuştu:
“–Kareleme yöntemiyle müşterilerimizi yerleştiriniz.”
Hiç kimse bir şey anlamamıştı. Müdür sordu:
“-Nasıl yani?”
“-Çok kolay” dedi başkan “$(1,1)$ deki müşteriyi $1$ numaraya,$ (1,2)$ dekini $2$ numaraya, $(2,2)$ dekini $3$ numaraya, $(2,1)$ dekini $4$ numaraya yerleştiriniz. Dikkat ederseniz tablomuzun sol üst köşesindeki ilk kareye ait sıralı çiftleri kullandık. Şimdi ikinci kareye geçelim. Karenin sağ üst köşesinden başlıyacağız. $(1,3)$ deki müşteriyi $5$ numaraya, $(2,3)$ deki müşteriyi $6$ numaraya, $(3,3)$ deki müşteriyi $7$ numaraya, $(3,2)$ deki müşteriyi $8$ numaraya, $(3,1)$ deki müşteriyi $9$ numaraya yerleştiriniz. Yine dikkat ederseniz, tablonun sol üst köşesindeki ikinci kareye ait bütün sıralı çiftleri kullandık. Artık böylece devam ediniz. Bakınız, örneğin, üçüncü kareye ait sıralı çiftleri, sağ üst köşeden sol alt köşeye doğru oklara gösterdiğim sırada yerleşeceksiniz. Sonra $4$-üncü, $5$-inci, $6$-ıncı, … kareler için de aynı işi yapacaksınız.”
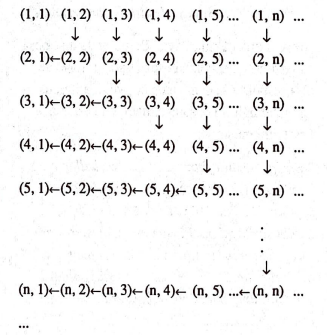
Müdür:
“-Acaba bu kez bütün müşteriler Kozmoz’a sığacak mı?”
diye kuşkuyla sordu.
“-Elbette” dedi başkan “Hem bütün müşteriler sığacak, hem de boş yer kalmayacak. Bakınız bu tablodan görüldüğü gibi, ilk $n$ tane otelin ilk $n$ odalarından gelecek $n^2$ müşteriyi Kozmoz’un ilk $n^2$ odasına yerleştirmiş olacaksınız. Bütün müşteriler er ya da geç bu karelerden birisine dahil olacaklardır; yani Kozmoz’a yerleşebileceklerdir. Örneğin, $217$ inci otelin $136$ numaralı müşterisi $217$ inci karede yerini alacaktır. Hatta, isterseniz hangi numaraya gideceğini de söyleyebilirsiniz. Bu müşteri $216^2+136$ numaralı odaya yerleşecektir. Genel bir kural olarak, $m$-inci otelin $n$-inci odasındaki müşteriyi, eğer $n \geq m$ ise Kozmoz’un $(n-1)^2+ m $numaralı odasına, eğer $n \leq m$ ise Kozmoz’un $(m^2-n+1)$ numaralı odasına yerleşecektir.”
Başkanın önerisini şimdi hepimiz iyice anlamıştık. Gerçekten hem bütün müşteriler Kozmoz’a sığıyor, hem de Kozmoz’un hiçbir odası boş kalmıyordu.
Pulsever matematikçi, LCR-287 galaksisine bir gezi kazanmış oldu.
Bu başarılı çözüm onuruna, otel müdürü o akşam bütün müşterilere bir davet verdi. Aksiliğe bakın ki, davette bile problemler çıkmaya başladı. Kozmoz’un tek numaralı odalarındaki müşteriler davete yarım saat geç geldiler. Baktılar ki, bütün sandalyeler, çift numaralı odaların müşterileri tarafından doldurulmuş durumda. Oysa, nazik otel müdürümüz herkese bir sandalye hazırlatmıştı. Neyse, artık otel katibi bile bu işin üstesinden gelebilirdi. Daha önceden edindiği bilgiye göre, sandalyelerdeki konukları uygun biçimde geriye kaydırarak yeni gelenlerin hepsine yer açtı. Hem de, dışarıdan tek bir sandalye bile getirmeden…
Biraz sonra konuklara dondurma sunuldu. Her konuğa ikişer külah dondurma düştü. Oysa, aşçıbaşı, herkese ancak birer külah hazırlamıştı. Sanıyorum ki, bunun nedenini, sizler de benim gibi kolayca anlayabilirsiniz.
Giderek, bu otelde olanaksız sandığımız her şeyin olabileceğine inanmaya başlıyordum ki, nazik dostuma, yeni bir buyruk daha ulaştı. Genel merkezden, müşterilerin, Kozmoz oteline kaç değişik biçimde yerleştirilebileceği soruluyordu. Her bir yerleşme biçimi, boş odalar $0$ ile dolu odalar $1$ ile gösterilmek üzere, bu iki rakamdan oluşan sonsuz bir satır dizisi ile temsil edilecekti. Örneğin, yalnız tek numaralı odaların dolu olduğu yerleşme biçimi
$1010101010 …$
dizisi ile; bütün odaların dolu olduğu yerleşme biçimi
$1111111111 …$
dizisi ile; bütün odaların boş olduğu durum (ki bu işletmenin iflası demektir) ise
$0000000000 …$
dizisi ile temsil edilecekti.
Otel müdürü problemi bir süre düşündükten sonra şöyle bir yol buldu. Otelin her katında sonsuz çoklukta oda vardı; yani otelin her bir katı, otelin bütün odaları kadar odaya sahipti. Dolayısıyla, her katın, sorumlusundan müşterileri kendi katına nasıl yerleştireceğini belirten bir liste istedi. Farklı iki kattan gelen listelerin aynı olmaması için de gerekli kontrolün yapılmasını buyurdu. Otelde sonsuz çokluktaki her kattan, yerleşme biçimini gösteren diziler yazılıp getirildi. Artık müdürün yapacağı iş bu dizileri alt alta yazıp meydana gelen listeyi ilgili yere göndermekti.
Dostuma,
“-Bu listenin tam olduğuna nasıl güveniyorsunuz? Acaba bu listedekilerden faklı bir yerleşme biçimi olamaz mı?”
diye sordum.
“-Doğrusu, bilemiyorum. Elimde sonsuz çoklukta yerleşme biçimi var. Öyleyse, bütün yerleşme biçimleri bu listede var olmalıdır diye düşünüyorum.”
dedi.
“Bu listenin tam olmadığını gösterebilirim. Size, elinizdekilerden farklı bir yerleşme biçimi bulacağım.”
dedim. Otel müdürü bana gülerek şöyle dedi:
“Dostum Mülayım, belki bu liste eksiktir. Ama bunun böyle olduğunu hiç kimse gösteremez. Zaten elimizde sonsuz çoklukta dizi var. Bundan ötesi nasıl olacak?”
Dostumla iddiaya girerek işe koyuldum. Önce her katın sorumlusuna önerdiği yerleşme biçimini ilgili odaların kapısına yazmalarını rica ettim. Yani, boş önerdikleri odaların kapısına $0$, dolu önerdikleri odaların kapısına $1$ yazmalarını istedim. Sonra birinci kattaki birinci odanın kapısına gittim. Kapıda $0$ vardı. Kuracağım dizinin ilk terimini $1$ olarak yazdım. Sonra ikinci kata çıktım. Bu kez bu katın ikinci odasının kapısındaki numaraya baktım: $1$ idi. Dizinin ikinci terimi olarak $0$ yazdım. Sonra üçüncü kata çıktım, üçüncü odanın kapısına baktım: $1$ idi. Dizimin üçüncü terimi olarak yine $0$ yazdım. Böylece her katta o katın numarasına eşit numaralı odanın kapısında$ 0$ mı, $1$ mi yazılı olduğuna bakıyor, $0$ ise listeme $1$, $1$ ise listeme $0$ rakamını yazıyordum. Böylece her katta dizimin bir teriminin ne olması gerektiğine karar veriyordum. Buna göre, örneğin, $778$ inci katta, yalnızca $778$ numaralı odanın kapısına bakıyorum; kapıda $0$ varsa, dizimin $778$ inci rakamını $1$ diye yazıyorum; $1$ varsa $0$ diye yazıyorum.
Bütün katlarda aynı işi yaptıktan sonra hazırladığım diziyi gururla müdürün önüne koydum:
“-İşte dostum” dedim “listende olmayan bir yerleşme biçimi ! “
“-Bunun benim listemde olmadığını nasıl bilebiliyorsun?”
“-Çok kolay!.. Kurduğum bu dizi, senin listedeki birinci dizi olamaz, çünkü ilk rakamları farklıdır. İkinci dizi de olamaz, çünkü bütün öteki terimler eşit olsa bile ikinci terimlerinin farklı olduğunu görüyoruz. Üçüncü diziye bakalım, üçüncü rakamlar farklıdır… Genel olarak, benim kurduğum dizi ile senin listedeki $n$-inci diziyi karşılaştıralım. Bu iki dizinin $n$-inci terimleri farklıdır, çünkü diziyi, özellikle, böyle olacak şekilde kurdum. Demek ki, bu dizi senin listedeki dizilerden hiçbirisine eşit değildir. “
Müdür, sonsuz çokluktaki listesinde yer almayan yeni bir dizi bulmamı, sanki gereksiz bir işgüzarlık olarak gördü:
“-Eh” dedi “öyleyse sizin diziyi de listeye ekleyelim, listemiz tam olsun. ” dedim “Bu liste hiçbir zaman tam olamaz… Bu diziyi listeye eklesen, ne değişecek? Gene elinde numaralanabilen sonsuz çoklukta bir diziler listesi olacak. O zaman, önceki yöntemi kullanarak, bu yeni listede de olmayan yeni bir dizi daha kurabilirim. Hem bu işin sonu hiç gelmez. Her seferinde, listede olmayan yeni bir dizi bulabilirim. ”
“-Yani, şimdi bu işin içinden çıkamadık, diye mi bildirelim merkeze?” diye sordu.
“-Hayır” dedim “tam tersine, sorunu çözümledik. Onların istediği gibi, müşterilerin Kozmoz’a mümkün yerleşme biçimlerini bir listeye sıralamak olanaksızdır. Matematiksel deyişle, bu yerleşme biçimlerini numaralamak; yani saymak olanağı yoktur. Daha açıkçası, sayılamaz çoklukta yerleşme biçimi vardır. “
Haber merkeze doğru yola çıkarken ben de nazik arkadaşım otel müdürüne veda ederek, emektar roketime atladım. Dönüşte, dostum Tarantog’a, o kara banttan daha çok, Kozmoz otelini, daha doğrusu sonsuz kümelerin karşılaştığım bu olağanüstü özelliklerini anlatacaktım.
UYARI. Bu noktada artık kahramanımız Mülayim’i rahat bırakalım ve ona fiziksel olarak olanaksız bildiğimiz bazı şeyleri nasıl başardığını sormayalım. Örneğin, görecelik (rölativite) kuramına göre 186.000 mil/sn den daha büyük bir hızla herhangi bir sinyal göndermek olanaksızdır. Dolayısıyla, otel müdürünün buyruklarının bütün odalara ulaşması bile sonsuz zamanı gerektirir. Başka bir deyişle, bu buyruklar hiçbir zaman her yere ulaşamayacaktır. Aynı şekilde, kahramanımızın sonsuz çokluktaki katları dolaşması da hiçbir zaman bitmeyecektir.
Bunda, bizim yapmak istediğimiz şey sonsuz kümeleri incelemektir. Dolayısıyla, fiziksel bakımdan olanaksız olan olayların nasıl olduğunu düşünmeyeceğiz.
Bu öykü aşağıdaki kitaptan alınmıştır:
Timur Karaçay: SOYUT MATEMATİĞE GİRİŞ, Modern Matematik ve Fen Kitapları, Milli Eğitim Basımevi, İstanbul, 1975.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

