Yazar: Halil İbrahim Karakaş
Yıl: 1992-3
Bir toplumun her bireyinin, Çeşitli konularda belli tercihleri vardır. Birey, önceden var olan veya kendisine sunulmuş olan seçenekler arasından kendisi için veya başkası için seçim yapar; yapılan bu seçime göre, bireyin veya başkalarının yaşantıları etkilenir. Çoğu zaman bir toplumun, bütün olarak, bir konuda alacağı karar ve göstereceği etkinlikler, toplumun bireylerinin o konuda yapacakları seçim ya da tercihlerle belirlenir. Başka bir deyimle, toplumun bir konudaki seçimi, bireylerin o konudaki seçimleriyle ortaya çıkar.
Toplumun ve bireylerin yarınları veya gelecekleri, bugün yaptıkları seçimlerle veya tercihlerle biçimlenir. Bu nedenle, seçim kavramı ve seçme eylemi üzerinde özenle düşünmekte, bunları irdelemekte, bir seçimin arzu edilen özelliklerinin neler olması gerektiğini araştırmakta yarar vardır.
Önce, seçme eylemi nedir, nasıl oluşur onu belirleyelim. Bir seçme eyleminden veya seçim olayından söz edebilmemiz için, her şeyden önce, bir seçenekler kümesi bulunmalıdır. Örneğin, konuk olduğunuz bir yerde size: “Ne içersiniz? Çay, kahve ve Kola var.” diye sorulursa, seçenekler kümesi
$$\{\text{cay, kahve, kola}\}$$
dır. Seçiminizi bu kümeden yaparsınız. Bu basit örnekte de görüldüğü üzere, seçim olayı, seçenekler kümesinin elemanları birbirleriyle karşılaştırılıp tercihlerde bulunarak gerçekleştirilir.
Yukarıdaki örnekte, ne içeceğinizi bildirirken, seçenekler kümesindeki içecekleri birbiri ile karşılaştırıp biri için tercihte bulunursunuz (veya bu eylemi daha önceleri yapmışsınızdır) örnek olarak, (çay, kahve) ikilisinden biri veya hiçbiri lehine tercihte bulunursunuz. Bunu (çay, kola) ve (kola, kahve) ikilileri için tekrarlarsınız. Yapacağınız seçimin, en azından kendi içinde tutarlı olması için, seçenekler kümesinin elemanlarını ikişer ikişer ele alıp tercihlerde bulunurken bazı kurallara uymanız gerekir. Örneğin, (çay, kahve) ikilisinden kahveyi tercih ediyorsanız (kahve, çay) ikilisinden de kahveyi tercih etmeniz gerekir (Ters-Simetri Özelliği). Eğer, (çay, kahve) den kahveyi (kahve, kola) dan kolayı tercih ediyorsanız, (çay, kola) dan hangisini tercih etmeniz gerekir? Kuşkusuz kolayı! (Geçişme Özelliği).
Konuyu matematiksel bir zemine çekmek için seçenekler kümesinden oluşturacağımız bir ikilinin her iki bileşeninin de aynı olması durumunda, o ikiliyi oluşturan elemanın tercih edileceğini varsayalım (Yansıma Özelliği). Örneğin, (çay, çay) ikilisinden, çay tercih edilecektir
Bu noktada bir yanlış anlama olasılığını ortadan kaldırmak için, bileşenleri farklı olan herhangi bir ikilinin hiçbirinin de tercih edilmeyebileceğini belirtmeyiz. Somut bir örnekle, (çay, kola) ikilisinden hiçbirini sevmeyebilirsiniz.
Şimdi, yukarıda söylediklerimizi matematiksel dile aktarmağa çalışalım. Bir seçim olayında, seçenekler kümesi $S$ ise, yapılan seçim, $S$’nin elemanlarından oluşan bazı ikililer, yani $S$’nin kendisi ile Kartezyen çarpımı, $S\times S$’nin bir altkümesine karşılık gelmektedir. Bu altküme,
$$K=\{(a,b)\in S\times S: \text{$a$, $b$’ye tercih ediliyor}\}$$
biçiminde tanımlanabilir.
İçecek örneğimize geri dönelim: çay yerine $c$, kahve yerine $k$ ve kola yerine $l$ yazarak
$$K_1=\{(c,c),(k,k),(l,l),(c,k),(c,l)\}$$
kümesini ele alalım. Bu küme $S=\{c,k,l\}$ olmak üzere $S\times S$’nin bir altkümesidir ve çay, kahve ve koladan çay tercih edildiğini göstermektedir.
Seçim olayında seçenekler kümesinden ikililer oluşturulurken, matematiksel deyimle, $S\times S$’nin $K$ altkümesi oluşturulurken bazı kurallara uyulması gerektiğini belirtmiştik. Bu kurallar
1. Her $a\in S$ için $(a,a)\in K$ (Yansıma Kuralı)
2. $a,b\in S$; $(a,b)\in K$ ve $(b,a)\in K \implies a=b$ (Ters-Simetri Kuralı)
3. $a,b,c\in S$; $(a,b)\in K$, $(b,c)\in K\implies (a,c)\in K$ (Geçişme Kuralı)
biçiminde ifade edilebilir. Böylece, bir seçenek kümesi üzerinde bir seçim yapmak, aşağıda verilen tanımlar çerçevesinde, bu seçenekler kümesi içinde bir kısmi sıralama bağıntısı oluşturmak demektir.
Tanımlar. Bir $S$ kümesi verilmiş olsun.
1) $S\times S$’nin her bir $K$ altkümesine $S$ içinde bir bağıntı denir.
2) $K$, $S$ içinde bir bağıntı ve
i) her $s\in S$ için $(s,s)\in K$ (Yansıma Özelliği)
ii) $s,t\in S$; $(s,t)\in K$, $(t,s)\in K\implies s=t$ (Ters-simetri Özelliği)
iii) $s,t,u\in S$; $(s,t)\in K$, $(t,u)\in K\implies (s,u)\in K$ (Geçişme Özelliği)
ise, $K$’ye $S$ içinde bir kısmi sıralama bağıntısı (kısaltılmış olarak kısıba) denir.
3) İçinde kısıba tanımlanmış bir kümeyi kısmi sıralanmış küme (kısaltılmış olarak ksk) denir.
Seçim sözcüğü çoğunlukla matematik sözcüğünden başka sözcükleri akla getirir: demokrasi gibi. Ancak, yukarıda sunulanlardan görüldüğü üzere, herhangi bir konuda bir seçim yapmak, belli bir küme içinde bir kısıba oluşturmak demektir. Bu, seçim sözcüğüne matematiksel bir anlam vermektedir. Sonuç olarak, “bir seçimin arzu edilen özellikleri neler olmalıdır?” sorusunu araştırırken, o seçimin seçenekler kümesi içindeki kısıbaları incelememiz gerektiğini görüyoruz.
Bu yazımızın kalan kısmında, ksklerle ilgili gösterimleri belirleyecek ve bazı özel ksklerden söz edeceğiz, ksk veya kısıbaların özelliklerini Matematik Dünyası’nın başka sayılarında ele alacağız.
Kuramsal olarak sonsuz ksklerden söz edilebilir, ancak biz seçimle ilgili tartışmalarımızda sadece sonlu kskleri ele alacağız; başka bir deyimle, ele aldığımız seçim olayında seçenekler kümesi sonlu olacaktır.
$S$ bir ksk olsun. $S$ içindeki kısıbayı $\geq$ ile gösterelim ve $a,b\in S$, $(a,b)\in\geq$ olması durumunda $a\geq b$ yazalım. $a\geq b$’yi “$a$, $b$’ye tercih edilmektedir” diye okuyabiliriz. Eğer $a\geq b$, fakat $a\neq b$ ise $a>b$ yazacağız. $c,d\in S$ için $c\not\geq d$ ve $c\not>d$ yazılımları, sırasıyla, $c\geq d$ ve $c>d$ olmadığını gösterirler.
Bir ksk, $S$’nin herhangi iki elemanı $a$ ve $b$ için
$$a>b,\,a=b\,,b>a$$
dan bir ve yalnız biri geçerli ise, bu takdirde $S$’ye tümden sıralanmış küme (kısaltılmış olarak, tsk) ve $\geq$’e de $S$ içinde bir tümden sıralama bağıntısı (kısaltılmış olarak, tüsiba) denir. Beraberlik durumunda kazananın bazı puanlama yöntemleri veya kura ile belirlendiği turnuvalar tskye örnek oluştururlar.
Beraberliğe izin verilen bir turnuva, tsk olmasa da ilginç bir ksk örneği oluşturur. Bu tür bir turnuvada iki oyuncu ya berabere kalmıştır ya da biri diğerine üstünlük sağlamıştır. Kısmi sıralanmış küme gösterimiyle, $a$ ve $b$’nin berabere kalmaları, “$a\not> b$ ve $b\not> a$” yazılarak ifade edilebilir.
$S$ bir ksk; $a,b\in S$, $a\not>b$ ve $b\not>a$ ise, bu takdirde $a$ ve $b$ ayrımsızdır denir ve $a\sim b$ yazılır. Ayrımsızlık, $S$ içinde yeni bir bağıntı verir. Bu bağıntı için, daima
-her $a\in S$ için $a\sim a$ (Yansıma Özelliği),
-$a,b\in S$, $a\sim b\implies b\sim a$ (Simetri Özelliği)
özellikleri geçerlidir. Eğer ek olarak,
-$a,b,c\in S$, $a\sim b$, $b\sim c \implies a\sim c$ (Geçişme Özelliği)
ise, bu takdirde $S$’ye zayıf sıralanmış küme (kısaltılmış olarak, zsk) ve $\geq$’e de $S$ içinde bir zayıf sıralama bağıntısı (kısaltılmış olarak, zasıba) denir.
Her tsk bir zskdir. zsk için bir başka örnek, satın alınacak bir eşyanın sadece fiyatına göre seçilmesidir.
Kısmi sıralanmış kümeler üzerine bazı ek koşullar öne sürerek değişik ksk örnekleri elde edilebilir. Bunlar değişik seçim yöntemlerine karşılık gelirler.
$S$ bir ksk ve $a,b\in S$ olmak üzere, eğer $c>a$ olacak biçimde hiç $c\in S$ yoksa, $a$’ya $S$’nin bir maksimal (büyükçe) elemanı denir. Benzer biçimde, $S$’nin $b>s$ olan hiç $s$ elemanı yoksa, $b$’ye $S$’nin bir $minimal$ (küçükçe) elemanı denir. Çoğu seçimlerde önemli olan, seçenekler kümesi $S$ ‘nin büyükçe veya küçükçe elemanlarını belirlemektir. Bunun yanında, her seçim olayında, ya her kskde, seçenekleri düzeylerine göre ayırmak mümkündür.
$S$ içinde $a_0>a_1>\dots>a_k$ biçiminde bir diziye uzunluğu $k$ olan bir dizi denir. Eğer $a\in S$ için $a_0>a_1>\dots>a_{k-1}>a_k>a$ biçiminde bir dizi varsa ve bu tür her dizinin uzunluğu $k$’den küçük veya $k$’ye eşit ise, bu takdirde $a$ elemanı k-ıncı düzeyde bir elemandır denir.
$a\in S$, $k$-ıncı düzeyde bir eleman ve
$$a_0>a_1>\dots>a_{k-1}=a$$
$a\in S$, $k$-ıncı düzeyde bir eleman ve
$$a_0>a_1>\dots>a_{k}=a$$
ise, $a_0$, $S$’nin büyükçe bir elemanıdır ve her $i=0,1,\dots,k-1$ için $a_i>s>a_{i+1}$ olacak biçimde hiç $s\in S$ yoktur.
$S$’nin toplam olarak $r$ elemanı varsa, $S$’nin en çok $r$-inci düzeyde elemanları vardır. Her $k=0,1,\dots,r-1$ için $S$’nin $k$-inci düzeyde elemanlarını belirlediğimizi ve bu elemanları, sıfırıncı düzey düzeyde olanlardan başlamak üzere, her düzeydeki elemanlar yatay bir sıra oluşturacak biçimde yukarıdan aşağıya doğru sıraladığımızı düşünelim. Ayrıca, $a > b$ ise $a$ ile $b$’yi bir doğru parçası ile birleştirelim. Bu yolla elde edilen çizelgeye $S$’nin Hasse Çizelgesi denir. Bir ksknin Hasse çizelgesi, onun tüm özelliklerini yansıtır.
Başlangıçta sunulan içecekler örneğinde, sıfırıncı düzeyde elemanlar kümesi $\{c\}$, birinci düzeyde elemanlar kümesi $\{k, l\}$ olup, daha yüksek düzeyde eleman yoktur. Böylece, içecekler örneğine karşılık gelen Hasse çizelgesi aşağıdaki gibidir:
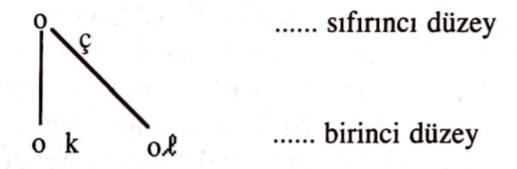
Bir ksknin bazı elemanları atılarak elde edilen bir altkümesi yine doğal olarak bir kskdir. Bu düşünce ile, bir ksk, $S$’nin elemanlarının düzeyleri belirlenirken şu yol izlenebilir: Önce $S$’nin büyükçe elemanları belirlenir, bunlar $S$’nin sıfırıncı düzeyde elemanlarıdır. Sonra, $S$’den büyükçe elemanların atılmasıyla elde edilen kümenin büyükçe elemanları belirlenir; bunlar $S$’nin birinci düzeyde elemanlarıdır. $S$’den tüm 0-ıncı, 1-inci,…, $(k-1)$-inci düzeyde elemanların atılmasıyla elde edilen alt kümenin büyükçe elemanları $S$’nin $k$-inci düzeyde elemanlarıdır.
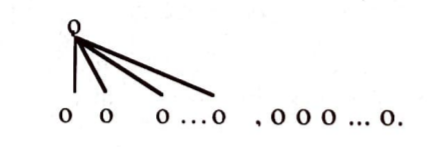
Somut bir örnekle yazımızı bitiriyoruz. Bir beldede belediye başkanlığı için yapılan seçimde $r$ aday bulunduğunu kabul edelim. Bu takdirde, her seçmen oyunu kullanırken (veya kullanmazken), bu $r$ elemanlı seçenekler kümesi içinde bir kısıba tanımlayacak ve böylece bu kümeyi bir kskye dönüştürecektir. Yaygın olarak uygulanan seçim yöntemlerinde, seçmenin, adaylardan sadece birini diğerlerine tercih etmesi istenir. Dolayısıyla, bir seçmenin belirleyeceği ksknin Hasse çizelgesi aşağıdakilerden biri olacaktır:
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı III. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Övünç Özgün Eker‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

