Yazar: Ali Nesin (California Üniversitesi (Irvine) Matematik Bölümü öğretim üyesi)
Yıl: 1995-1
Sayı: 21
Yoksulluk Kader Değil
Bu dizinin son bölümünde yoksulu kazandıracağız. Küçük bir olasılıkla da olsa, yoksul kazanabilecek.
İki oyuncu yazı-tura oynuyorlar. İlk yazı-tura atışında ortaya 1 lira konuluyor. Oyunculardan biri, diyelim birinci oyuncu, kaybettikçe ortaya koyduğu parayı arttırıyor, bir önceki atışta kaybettiğinin iki katını koyuyor. Kazandığındaysa ortaya 1 lira koyuyor. Örneğin ilk atışta kaybederse, ikinci atışta ortaya 2 lira koyuyor. İkinci atışta da kaybederse, üçüncü atışta 4 lira koyuyor. Kazanana değin bu böyle sürüyor. Kazandığında gene 1 lira ortaya koyuyor. Birinci oyuncu stratejisini sürdürebildikçe sürdürüyor. Sürdüremediğinde, yani cebinde yeterli parası kalmadığında, oyun bitiyor. Bu dizinin ilk yazısında, iki oyuncunun da sonlu parası olduğunda oyunun uygulamada kesinlikle biteceğini kanıtlamıştık. Aynı oyunu oynayacağız. Ancak bu kez ikinci oyuncunun sonsuz parası olduğunu varsayacağız (zengin oyuncu). Birinci oyuncununsa yalnızca 1 lirası var (yoksul oyuncu). Yoksul, yukarıda açıkladığımız stratejiyle oynuyor. Eğer stratejisini sürdüremezse oyun bitiyor, oyun daha önce bitemez. Zenginin parası hiç bitmediğinden, zenginin oyunu kaybetme olasılığı yoktur.
Daha ilk yazı-tura atışında yoksul kaybederse, yoksul cebindeki tek lirayı kaybeder ve oyun hemen biter. Dolayısıyla en az 1 / 2 olasılıkla yoksul oyunu kaybedecektir. Yoksulun oyunu kaybetme olasılığını bulamadım. Yazının sonunda bu olasılığı bulmak için hesaplanması gereken bir sayıyı vereceğim.
Yoksul ilk atışta kazanıp ikinci atışta kaybederse ne olur? Oyun gene biter, ama bu kez yoksulun cebinde 1 lirası vardır. Yani yoksul ‘tapi’ kalkar. Çünkü birinci yazı-tura atışında kazanmıştır, dolayısıyla ikinci atıştan önce cebinde 2 lirası vardır. İkinci atışta kaybettiğinden 1 lirası kalmıştır. Bu kez ortaya 2 lira koyması gerekmektedir ve 2 lira koyacak parası yoktur. Demek ki en az $1/4$ olasılıkla yoksul oyundan ne kazançlı ne de zararlı kalkar. Yoksulun oyundan ne kazancı ne de zararlı kalkma olasılığını da bulamadım.
Daha önceki bölümlerdeki oyunların tersine bu oyunda yoksul kazanabilir. Öyle bir an gelebilir ki, yoksulun cebinde 1 liradan fazla para olmasına karşın, yoksul stratejisini sürdüremez (yani oyun biter). Örneğin, yoksul ilk dört atışta kazanır da sonraki iki atışta kaybederse yoksulun cebinde 2 lira olmasına karşın oyun biter. Okur bu savımı kendi kendine kolaylıkla doğrulayabilir. Demek ki en az $1 / 2^{6}=1 / 64$ olasılıkla yoksul oyundan kazançlı ayrılır. Yoksulun oyundan $k$ lira kazançlı kalkma olasılığını da bilmiyorum${ }^{1}$.
Bu oyun sonsuza dek sürebilir, örneğin fakir hep kazanırsa … Ama göreceğiz ki oyunun sonsuza dek sürebilme olasılığı 0’dır. Bunu kanıtlayabildim! Dolayısıyla oyun $\%$ 100 (yani 1) olasılıkla biter. Demek ki oyun kuramsal olarak sonsuza dek sürebilse bile, uygulamada sonlu sayıda yazı-tura atışından sonra biter${ }^{2}$. Bu bölümde işte bu sonucu kanıtlayacağız.
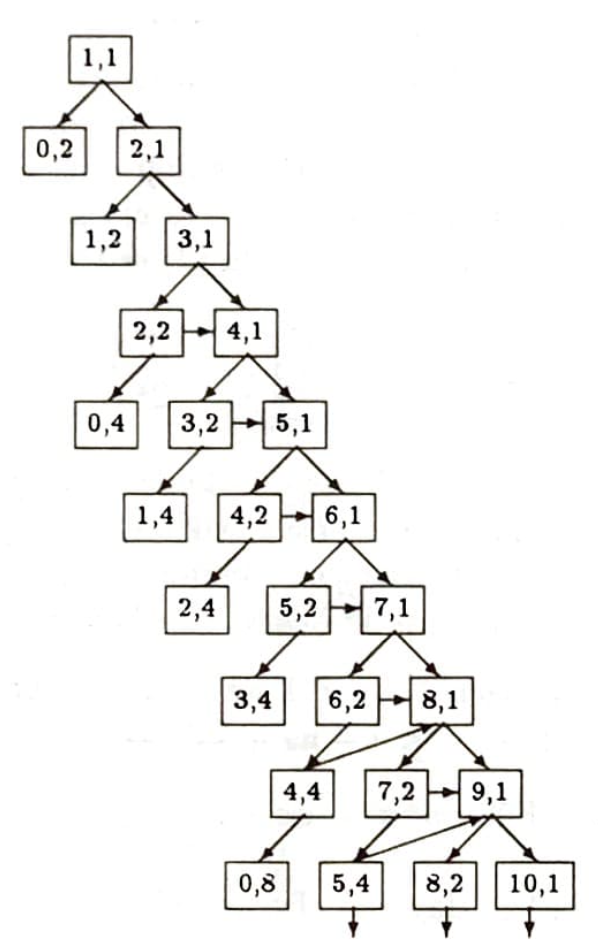
Oyunun ilk anlarda alabileceği durumları gösteren bir şema çizeceğiz. Önce oyunun alabileceği durumlarını saptayalım. Oyunun her durumunu iki sayıyla gösterebiliriz. Birinci sayı, yoksulun cebindeki para olsun; ikinci sayıysa bir sonraki atış için ortaya koyulan (daha doğrusu yoksulun koyması gereken) para olsun. İkinci sayı hep 2’nin üstleri olmak zorunda, $1,2,4,8,16$ gibi. Oyunun en başındaki durum $(1,1)$ durumu. Çünkü, yoksul oyuna 1 lirayla başlıyor ve ilk atışta ortaya 1 lira koyuyor. Bu durumda yoksul kazanırsa oyun $(2,1)$ durumuna geçecek, kaybederse de $(0,2)$ durumuna (ve oyun bitecek). $(2,1)$ durumundan sonra oyun ya $(1,2)$ durumuna ya da $(3,1)$ durumuna erişir. Birinci şıkta oyun biter, ikinci şıkta sürer. Eğer bir durumdan sonra oyun bitmemişse, oyun iki durumdan birini alır: yoksul o atışta ya kazanmıştır ya da kaybetmiştir. Oyunun ilk birkaç yazı-tura atışında alabileceği durumlar yukarıda görülüyor.
Yukarıda da dediğimiz gibi oyunun sonsuza değin sürme olasılığının 0 olduğunu kanıtlayacağız. $\left(n, 2^{k}\right)$ durumuna gelme olasılığına $p\left(n, 2^{k}\right)$ diyelim. Örneğin, $$ \begin{split}
& p(1,1)=1 \\
& p(0,2)=1 / 2 \\
& p(2,1)=1 / 2 \\
& p(1,2)=1 / 4 \\
& p(3,1)=1 / 4\\
& p(2,2)=1 / 8 \\
& p(4,1)=1 / 8+1 / 16=3 / 16 \\
& p(0,4)=1 / 16 \\
& p(3,2)=1 / 16+1 / 32=3 / 32 \\
& p(5,1)=1 / 16+2 / 32+1 / 64=9 / 64
\end{split} $$
Oyunun sonsuza gidebilmesi için bütün $(n, 1)$ durumlarına ulaşılmalıdır. Bu, şemadan kolayca anlaşılıyor. Demek ki oyunun sonsuza dek sürebilme olasılığı, $p(n, 1)$ dizisinin $n$ sonsuza gittiğinde aldığı değerdir. Dolayısıyla
$$\lim _{n \rightarrow \infty} p(n, 1) $$ sayısını hesaplamamız gerekiyor. Bu sayının 0 olduğunu göreceğiz. Bu limitin sıfır olduğunu kanıtlamak için, aşağıdaki eşitliği bulmak yeterlidir: $$\lim _{n \rightarrow \infty} p\left(2^{n}-1,1\right)=0 $$
Bu son eşitliği kanıtlamak daha kolay olacak.
$p\left(n, 2^{k}\right)$ sayılarını bulmak istiyoruz. Bunun için biraz matematik yapmalıyız. Yapacağımız matematiği daha iyi anlaması için, okurun sık sık yukarıdaki şemaya bakması gerekecektir. İlk olarak, eğer $k>0$ ise,
$$ p\left(n, 2^{k}\right)=\frac{p\left(n+2^{k-1}, 2^{k-1}\right)}{2} \tag{1} $$ eşitliğine dikkatinizi çekerim. Çünkü, eğer $k>0$ ise, $2^{k}>1$ ‘dir ve dolayısıyla $\left(n, 2^{k}\right)$ durumuna gelmenin bir tek yolu vardır, o da bir önceki oyunda kaybetmiş olmak. Bir önceki oyunun durumu ne olabilir? $\left(n, 2^{k}\right)$ durumunda ortaya $2^{k}$ koyduğumuza göre, bir önceki oyunda ortaya $2^{k-1}$ koymuşuzdur (ve kaybetmişizdir). Dolayısıyla $\left(n, 2^{k}\right)$ durumuna ancak $\left(n+2^{k-1}, 2^{k-1}\right)$ durumundan geçilebilir. $(1)$ eşitliği işte bu yüzden geçerlidir. $(1)$ eşitliğinde $k$ yerine $k-1$ ve $n$ yerine $n+2^{k-1}$ koyarsak $$ p\left(n+2^{k-1}, 2^{k-1}\right)=\frac{p\left(n+2^{k-1}+2^{k-2}, 2^{k-2}\right)}{2} $$ eşitliği çıkar. Bu son eşitliği $(1)$’in sağ tarafına yerleştirerek, $$ p\left(n, 2^{k}\right)=\frac{p\left(n+2^{k-1}+2^{k-2}, 2^{k-2}\right)}{4} $$ eşitliğini elde ederiz. Bunu böylece sürdürürsek, $$ p\left(n, 2^{k}\right)=\frac{p\left(n+2^{k-1}+2^{k-2}+\cdots+2+1,1\right)}{2^{k}} $$ eşitliği elde edilir. Bu eşitlikteki $2^{k-1}+2^{k-2}+\cdots+2+1$ sayısı $2^{k}-1$ sayısına eşit olduğundan, eğer $k>0$ ise, $$ p\left(n, 2^{k}\right)=\frac{p\left(n+2^{k}-1,1\right)}{2^{k}} \tag{2} $$ eşitliği geçerlidir. $(2)$ eşitliğinden, $p\left(n, 2^{k}\right)$ sayılarını bulmak için, $p(n, 1)$ sayılarını bulmamız gerektiği anlaşılıyor. Bu sayıları bulalım. $(n, 1)$ durumuna ancak kazanarak gelinir. Yani $(n-1,1),(n-2,2),(n-4,4)$ gibi durumlardan. Dolayısıyla $p(n, 1)$ sayısı, $$ \frac{p(n-1,1)}{2}, \frac{p(n-2,2)}{2}, \frac{p(n-4,4)}{2}, \ldots $$ sayılarının, yani, bir $k$ için, $p\left(n-2^{k}, 2^{k}\right) / 2$ biçiminde yazılabilen sayıların toplamıdır. (2) eşitliği $p\left(n-2^{k}, 2^{k}\right)=p(n-1,1) / 2^{k}$ eşitliğini verdiğinden, $p(n, 1)$ sayısının $p(n-1,1) / 2^{k+1}$ sayılarının toplamı olduğu anlaşılır. Ama buradaki $k$ sayıları $n-2^{k} \geq 2^{k}$ koşulunu, yani $2^{k+1} \leq n$ koşulunu sağlamalıdır, çünkü aksi halde $\left(n-2^{k}, 2^{k}\right)$ durumunda oyun bitmiştir ve bu durumdan $(n, 1)$ durumuna geçilmez. $k(n)$, $2^{k} \leq n$ eşitsizliğini sağlayan $k$ sayılarının en büyüğü olsun. Demek ki $$ \begin{split}
p(n, 1) & =\sum_{k=1}^{k(n)} \frac{p(n-1,1)}{2^{k}} \\
& =p(n-1,1) \sum_{k=1}^{k(n)} \frac{1}{2^{k}} \\
& =p(n-1,1)\left(1-\frac{1}{2^{k(n)}}\right) .
\end{split} $$
Bu eşitliği $n-1$ kez kullanarak, $$ p(n, 1)=p(1,1) \prod_{i=2}^{n}\left(1-\frac{1}{2^{k(i)}}\right) $$ buluruz. Ama $p(1,1)=1$. Burada $n$ yerine $2^{n}-1$ alırsak, $$ p\left(2^{n}-1,1\right)=\prod_{i=2}^{2^{n}-1}\left(1-\frac{1}{2^{k(i)}}\right) \tag{3} $$
buluruz. Şimdi $k$ herhangi bir doğal sayı olsun. Hangi $i$ sayıları için $k(i)=k$ ȩ̧itliğinin doğru olduğunu bulalım. $i$, $k(i)=k$ eşitliğini sağlayan bir sayı olsun. $k$ sayısı, $2^{k} \leq i$ eşitsizliğini sağlayan sayıların en büyüğü olduğundan $2^k \leq i<2^{k+1}$ eşitsizliği geçerlidir. Ve bunun tersi de doğrudur: eğer $2^{k} \leq i<2^{k+1}$ ise, $k(i)=k$ eşitliği geçerlidir. Bu eşitsizlikleri sağlayan kaç tane $i$ sayısı vardır? Biraz düşünme, $2^{k}$ tane olduğunu gösterir. $(3)$ eşitliğinin sağındaki çarpılacak terimler bu $2^{k}$ tane $i$ sayısı için birbirlerine eşittirler. Dolayısıyla $(3)$ eşitliğini, $$ p\left(2^{n}-1,1\right)=\prod_{k=1}^{n-1}\left(1-\frac{1}{2^{k}}\right)^{2^{k}}\tag{4} $$ olarak yazabiliriz. Bu eşitliği kullanarak $p\left(2^{n}- 1,1\right)$ sayılarının $n$ sonsuza gittiğinde sıfıra yakınsadıklarını kanıtlayacağız. Bunun için konumuzdan biraz uzaklaşıp iki önsav kanıtlayacağız:
Önsav 1. Eğer $00$ bir doğal sayıysa, $(1-x)^{n} \leq 1-n x+\frac{n(n-1)}{2} x^{2}$.
Kanıt. Eğer $n=1$ ise önsav elbette doğru. Şimdi önsavın $n$ için doğru olduğunu varsayıp $n+1$ için kanıtlayalım. Demek ki $$(1-x)^{n} \leq 1-n x+\frac{n(n-1)}{2} x^{2}$$ eşitliğini biliyoruz, daha doğrusu varsayıyoruz. Her iki tarafı da $1-x$ ile çarpalım: $0<1-x$ olduğundan, sağ tarafı açacak olursak, $$(1-x)^{n+1} \leq 1-(n+1) x+\frac{n(n+1)}{2} x^{2}-\frac{n(n+1)}{2} x^{3}$$ buluruz. $x>0$ olduğundan, $$ (1-x)^{n+1}<1-(n+1) x+\frac{n(n+1)}{2} x^{2} $$ elde ederiz. Demek ki önsav $n+1$ için doğru. Tümevarımla önsav her doğal sayı için doğrudur. Önsavımız kanıtlanmıştır. $\qquad \square$
Önsav 2. $k \geq 1$ ise, $\left(1-\frac{1}{2^{k}}\right)^{2^{k}}<\frac{1}{2}$.
Kanıt. Üstteki önsavda $x=1 / 2^{k}$ ve $n=2^{k}$ alalım.
$$ \left(1-\frac{1}{2^{k}}\right)^{2^{k}} \leq 1-2^{k}\left(\frac{1}{2^{k}}\right)+\frac{2^{k}\left(2^{k}-1\right)}{2}\left(\frac{1}{2^{2 k}}\right) $$ elde ederiz. Sağ taraftaki ilk iki terim sadeleşir. En sağdaki terimi hesaplayalım:
$$ \frac{2^{k}\left(2^{k}-1\right)}{2^{2 k+1}}=\frac{2^{k}-1}{2^{k+1}}=\frac{1}{2}-\frac{1}{2^{k+1}}<\frac{1}{2} $$
İkinci önsav da kanıtlanmıştır ${ }^{3}$. $\qquad \square$
Şimdi $(4)$’teki sayıların sıfıra yakınsadığını kanıtlayabiliriz. İkinci önsavı ve $(4)$ eşitliğini kullanarak, $p\left(2^{n}-1,1\right) \leq 1 / 2^{n-1}$ buluruz. $n$ sonsuza gittiğinde sağdaki terimler 0’a yakınsadığından, $p\left(2^{n-1}, 1\right)$ sayıları da sıfıra yakınsar. Demek ki oyunun sonsuza dek sürme olasılığı 0’dır, ve oyun 1 olasılıkla biter.
Oyundan yoksulun zararlı (yani 0 lirayla) kalkma olasılığı nedir? Bu olasılığı bulmak için $p\left(0,2^{k}\right)$ sayılarını toplamalıyız. $$ p_{0}=\sum_{k=1}^{\infty} p\left(0,2^{k}\right) $$ olsun. $p_{0}$, yoksulun oyundan zararlı kalkma olasılığıdır. $(2)$ eşitliğinde $n=0$ alırsak, $p\left(0,2^{k}\right)=p\left(2^{k}-1,1\right) / 2^{k}$ buluruz. $(4)$ eşitliğini de kullanarak, $$ p\left(0,2^{k}\right)=\frac{1}{2^{k}} \prod_{i=1}^{k-1}\left(1-\frac{1}{2^{i}}\right)^{2^{i}} $$ elde ederiz. Dolayısıyla, $$ p_{0}=\sum_{k=1}^{\infty} \frac{1}{2^{k}} \prod_{i=1}^{k-1}\left(1-\frac{1}{2^{i}}\right)^{2^{i}} $$ olur. Bu sayıyı hesaplayamadım.
${ }^{1}$ Bu hesaplayamadığım olasılıkların yaklaşık hesaplanabilmesi için gereken malzeme bu yazıda vardır. Dileyen okur bu sayıları yaklaşık hesaplayabilir. Bu tam olarak hesaplayamadığım olasılıklar henüz ad verilmemiş sayılar da olabilirler. Sözcük sayımız sonsuz ama yalnzca sayılabilir sonsuzlukta. Gerçel (reel) sayılarsa sayılamaz sonsuzlukta. Dolayısıyla her sayıya ad veremeyiz. Önemli bulduğumuz sayılara ad veririz. Örneğin $\pi$ sayısı önemli olduğundan $\pi$’ye bir ad verilmiştir: $\pi$. $\pi$’nin karesinin ve karekökünün de adları vardır: $\pi^2$ ve $\sqrt{\pi}$. Tam olarak hesaplayamadığım bu üç olasılığa daha önce bir ad verilmiş midir bilmiyorum. Verilmemişse hiçbir zaman tam olarak hesaplayamayı. Nasıl $\pi$’nin kaç olduğunu hiçbir zaman tam olarak bilemeyeceksek ve ancak adın söyleyerek $\pi$’nin kimliğini belirtebiliyorsak, bu sayıları da hiçbir zaman bilemeyebiliriz, hatta daha önceden adı konmuş sayılarla arasında cebirsel bir bağıntı bile olmayabilir. Özet olarak demek istediğim, bu sayıların tam olarak hesaplanamayabilecekleri. Bu bağlamda akla gelen ilk soru şu: hesaplayamadığım olasılıklar kesirli sayılar mıdır? Pek sanmıyorum.
${ }^{2}$ Bu oyunun 1 olasılıkla bitmesi yoksulun cebindeki paraya bağlı değildir. Şemadan da anlaşılacağı üzere, yoksulun cebinde 1 lira olduğunda oyun 1 olasılıkla biterse, yoksulun cebinde kaç para olursa olsun oyun gene 1 olasılıkla biter.
${ }^{3}$ Bu önsavın doğruluğu biraz analizle de çıkabilir. $\left(1-1 / 2^{k}\right)^{2^{k}}$ sayılarının $1 / e$ sayısından (dolayısıyla $1 / 2$ sayısından da) küçük oldukları analiz kullanarak kolaylıkla kantlanabilir.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

