Yıl: 2014-2
Sayı: 99
Geçen sayıda başladığımız Lineer Cebir konusuna “determinantlar” ile devam ediyoruz. Zaman zaman, geçen sayıda bahsettiklerimize başvuracağız; bunu yaparken oradaki numaralandırmayı yapacağız. Yani elinizin altında MD 2014-1’i tutmanızda fayda var.
Verilen bir $n > 0$ için $n \times n$’lik matrislerden oluşan kümeyi $M_n$ ile gösterelim. Bu kümeden alınan $A= ( \, a_{ij} )$ ve $B=( \, b_{ij} ) \, $ matrisleri ve bir $r \in \mathbb{R}$ için $$A+B=( \, a_{ij}+b_{ij} ) \, \quad \text { ve } \quad rA=( \, ra_{ij} )\,$$
olarak tanımlanır. Bu işlemlerle $M_n$ bir vektör uzayı olur. Aslında biz burada $M_n$’nin vektör uzayı yapısıyla ilgilenmeyeceğiz, ama vektör uzayı örneklerimize eklemekte fayda var.
Determinant, $M_n$’den $\mathbb{R}$’ye giden, çeşitli özellikleri sağlayan bir fonksiyon olacak. Yani her $n$ için ayrı bir fonksiyon olacak ama biz bunların hepsini “$\operatorname{det}$” ile göstereceğiz. Hemen şunu da belirtelim: Determinant lineer bir fonksiyon olmayacak.
Determinant, birçok yerde karşımıza çıkan bir kavram, ama şimdilik sadece şu özelliğinden bahsedelim: $A \in M_n$ matrisinin tekil olmaması için gerek ve yeter koşul $\operatorname{det} A \neq 0$ olmasıdır. Bu noktada tekil olmayan bir matrisin ne demek olduğunu hatırlayalım: Eğer $A$’yı indirgenmiş eşelon forma dönüştürdüğümüzde birim matrisi elde ediyorsak $A$’ya tekil değildir denir. Yani elde etmek isteyeceğimiz fonksiyon birim matriste $0$’dan farklı bir değer almalı ve Gauss hamleleri matrislerin determinantlarının $0$ olup olmadığını etkilememeli. Bunlar çok muğlak gözlemler ancak buraya sadece determinant fonksiyonunun ne tür temel özellikler sağlaması gerektiğini anlamaya çalışıyoruz. Bu temel özellikleri anlamak için ilk önce küçük boyutlu (yani $2 \times 2$’lik ve $3 \times 3$’lük) matrislerde gözlemler yapalım.
$2 \times 2$ Matrislerin Determinantı. MD 2014-1 sayısındaki Sonuç 4’ü hatırlayalım:
$$ \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} \text{ tersinirdir } \Leftrightarrow ad-cb \neq 0.$$ Bu durumda $$ \operatorname{det} \begin{pmatrix} a & b \\ c & d \end{pmatrix} = ad-bc $$ olarak tanımlayacağız.
Tanımladığımız bu fonksiyonun Gauss hamleleriyle nasıl değiştiğine bakalım.
- Bir satırın $k$ katını bir başka satıra ekleme: İlk satırın $k$ katını ikinciye ekleyelim. Elde ettiğimiz matris $$\begin{pmatrix} a & b \\ ka+c & kb +d \end{pmatrix}$$ ve bu matrisin determinantı $$( \, kb+d ) \, -b ( \, ka+c ) \, = kab+ad-kab-bc=ad-bc.$$ Bu işlem determinantı değiştirmedi. İkinci satırın $k$ katını ikinciye eklediğimiz durumda da determinantın değişmediğini benzer biçimde görebiliriz.
- Bir satırı, sıfır olmayan bir $k$ ile çarpmak: İlk satırı $k$ ile çarpalım: $$\begin{pmatrix} ka & kb \\ c & d \\ \end{pmatrix}.$$ Bu matrisin determinantı $kad-kbc=k ( \, ad-bc ) \,$ oluyor. Yani bu işlemin etkisi determinantı $k$ ile çarpmak oluyor.
- İki satırın yerini değiştirmek: bu durumda elde ettiğimiz matris de $$\begin{pmatrix} c & d \\ a & b \\ \end{pmatrix}$$ oluyor ve determinantı $cb-da= -( \, ad-bc )\,.$ Bu işlemin etkisi de determinantı $-1$ ile çarpmak.
- Eşelon Formdaki Matrislerin Determinantı: Bu matrislerde $c=0$ oluyor. Yani determinantları köşegen üzerindeki değerlerin çarpımı olarak elde ediliyor.
- Birim Matrisin Determinantı: Birim matrisin determinantının $1$ olduğuna da dikkat edelim. Daha sonra bunu kullanacağız.
$3 \times 3$ Matrislerin Determinantı. $3 \times 3$ ‘lük bir matris alalım: $$\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{pmatrix}.$$ Bu tür matrislerin determinantı $$aei-afh-bdi+bfg+cdh-ceg$$ olarak tanımlanır.
Şimdi $2 \times 2$ matrislere uyguladığımız adımları $A$ matrisine de uygulayalım ve determinantının nasıl etkilendiğini inceleyelim.
- Bir satırın $k$ katını bir başka satıra ekleme: Mesela ilk satırın $k$ katını üçüncüye ekleyelim: $$\begin{pmatrix} a & b & c \\ d & e & f \\ g+ka & h+kb & i+kc \\ \end{pmatrix}.$$ İşlemleri yaptığımızda bu yeni matrisin determinantının $\operatorname{det} A$ ile aynı olduğunu görürüz.
- Bir satırı sıfır olmayan bir $k$ ile çarpmak: İkinci satırı $k$ ile çarpalım: $$\begin{pmatrix} a & b & c \\ kd & ke & kf \\ g & h & i \\ \end{pmatrix}.$$ Bu matrisin determinantı $$\begin{split} & kaei-kafh-kbdi+kbfg+kcdh-kceg \\ &= k ( \, aei-afh-bdi+bfg+cdh-ceg )\, \end{split} $$ oluyor. Aynen $2 \times 2$’lik matrislerde olduğu gibi burada da verilen matrisin bir satırını $0$’dan farklı bir $k$ ile çarpmak, matrisin determinantının aynı $k$ ile çarpılmasına neden oldu.
- İki satırın yerini değiştirmek: Eğer ikinci ve üçüncü satırların yerlerini değiştirirsek elde edeceğimiz determinant. $$afh-aei-bfg+bdi+cge-cdh$$ olur. Bu da başladığımız determinantın $-1$ katıdır. Son iki özellik de aynen $2 \times 2$’lik matrislerdeki gibi.
- Eşelon formdaki Matrislerin Determinantı: Bu determinant köşegen üzerindeki değerlerin çarpımıdır. (Kontrol ediniz.)
- Birim Matrisin Determinantı: Birim matrisin determinantı $1$ olur.
Örnek 1. Burada $3 \times 3$’lük bir matrisin determinantını ‘formüllü’ tanımı kullanmadan, sadece yukarıdaki kuralları kullanarak hesaplayalım. Matrisimiz şu olsun: $$A= \begin{pmatrix} -1 & 1 & 2 \\ 0 & -1 & 1 \\ 2 & 0 & -1 \\ \end{pmatrix}.$$ Bu matrisin determinantını bulurken şu yolu izleyeceğiz: İlk önce $A$’yı eşelon forma getirelim (bu şekilde elde edeceğimiz matrisin determinantını nasıl bulacağımızı 4’ten biliyoruz), sonra da attığımız adımları tersine doğru takip ederek $A$’nın determinantını bulalım. \[ \begin{split} &\begin{pmatrix} -1 & 1 & 2 \\ 0 & -1 & 1 \\ 2 & 0 & -1\, \\ \end{pmatrix} \\ \overset{\text{2 }\rho_{1} + \rho_{3}} {\longrightarrow} &\begin{pmatrix} -1 & 1 &\;\,2\;\, \\ 0 & -1 & 1 \\ 0 & 2 & 3 \\ \end{pmatrix} \\ \overset{\text{2 }\rho_{2} + \rho_{3}} {\longrightarrow} &\begin{pmatrix} -1 & 1 & \;\,2\,\; \\ 0 & -1 & 1 \\ 0 & 0 & 5 \\ \end{pmatrix}. \end{split} \] Elde ettiğimiz bu son matrisin köşegenlerinin altındaki girdilerin hepsi $0$. Yani 4’ten dolayı, o matrisin determinantı köşegen girdilerinin çarpımı, yani $5$. Fakat uyguladığımız adımlarının ikisi de determinantı değiştiren adımlar değil. O halde $\operatorname{det} A=5$.
Aslında, herhangi bir matrisi eşelon forma getirmek için sadece bir satırın skaler katını başka bir satıra ekleme ve iki satırın yerini değiştirme işlemleri kullanılıyor (yani bir satırı bir skalerle çarpma sadece indirgenmiş eşelon forma çevirmek için gerekli). Bu durumda da en sonda elde edilen matrisin determinantı başladığımız matrisin determinantından sadece işaretle farkedebilir.
Örnek 2. Şimdi şu matrise bakalım: $$B= \begin{pmatrix} 0 & 1 & -2 \\ 0 & -1 & 1 \\ 1 & 1 & 3 \\ \end{pmatrix}$$ Sırasıyla şu işlemleri yaptığımızda $B$’yi eşelon forma dönüştürebiliriz: $\rho_{1}+\rho_{2}$, $\rho_{1} \leftrightarrow \rho_{3}$, $\rho_{2} \leftrightarrow \rho_{3}$. Bu işlemler sonucunda elde ettiğimiz matris şu olur: $$C= \begin{pmatrix} 1 & 1 & 3 \\ 0 & 1 & -2 \\ 0 & 0 & -1 \\ \end{pmatrix}.$$ İki kere satırları değiştirme işlemi kullandığımız için $$\operatorname{det} B= ( \, -1 ) \, ( \, -1 ) \,\operatorname{det}C= ( \, -1 ) ( \, -1 ) ( \, -1 ) = -1. $$
Örnek 3. Son olarak şu örneğe bakalım: $$D= \begin{pmatrix} 1 & 1 & -1 \\ 0 & -1 & 3 \\ -3 & -2 & 0 \\ \end{pmatrix}$$ Burada da sırasıyla $3 \rho_{1} + \rho_{3}$ ve $\rho_{2} + \rho_{3}$ hamleleri kullanılarak şu matris elde edilir: $$\begin{pmatrix} 1 & 1 & -1 \\ 0 & -1 & 3 \\ 0 & 0 & 0 \\ \end{pmatrix}.$$ Bu matrisin determinantı $0$ ve $D$’nin bu matrise denk olması tekil olduğunu söylüyor. yani $D$’nin tersi yok. Determinantların teorisini genel haliyle geliştirdiğimizde kare bir matrisin tersinir olup olmadığını kontrol etmek için çok kullanışlı bir yol determinantının $0$ olup olmadığını kontrol etmek olacak.
$n \times n$ Matrislerin Determinantı. Yukarıda $2 \times 2$ ve $3 \times 3$ matrislerde yaptığımız gözlemler ışığında determinantı kuru bir formülle tanımlamaktansa çeşitli özellikleri sağlayan bir fonksiyon olarak tanımlayacağız ve böyle bir fonksiyonun varlığını göstereceğiz. Hatta böyle fonksiyonlardan sadece bir tane olduğunu da göreceğiz.
Tanım 1. bir $n>0$ için $d_n : M_n \rightarrow \mathbb{R}$ fonksiyonu verilsin. Eğer $d_n$ aşağıdaki özellikleri sağlıyorsa bir determinanttır denir:
- Eğer $B$, $A$’nın bir satırının bir skaler katının başka bir satırına eklenmesiyle elde edildiyse, $$d_n ( \,B) \, = d_n ( \,A) \,.$$
- Eğer $B$, $A$’nın bir satırının bir $r$ skaleriyle çarpılmasıyla elde edildiyse, $$d_n ( \,B) \, = rd_n ( \,A) \,.$$
- $d_n ( \,I_n) \, =1.$
Şimdilik böyle bir fonksiyonun ne varlığını ne de tekliğini biliyoruz ama bir süre sanki biliyormuş gibi davranalım; $d_n$ yerine “$ \operatorname{det}$” notasyonunu kullanalım. Sadece bu üç kural kullanılarak determinant hesaplamayı kolaylaştıracak birtakım özellikler bulacağız.
Önsav 1. Aşağıdaki önermeler doğrudur:
- Eğer $B$, $A$’nın iki satırının yerinin değiştirilmesiyle elde edildiyse, $$ \operatorname{det} B =-\operatorname{det} A $$ olur.
- Eğer bir matrisin iki satırı aynıysa determinantı $0$’dır.
- Bir satırı tamamen $0$ olan bir matrisin determinantı $0$’dır.
- Bir matrisin tekil olmaması için gerek ve yeter koşul determinantının $0$ olmamasıdır.
Kanıt: İlk önermeyi kanıtlamak için –örneğin– $A$’nın ilk iki satırının yerlerinin değiştirilmesiyle elde edilmiş bir $B$ matrisi alalım. Amacımız $B$’yi diğer iki Gauss Hamlesiyle elde etmek. Bu hamleler sırasıyla şöyle: $\rho_{1} +\rho_{2}$, $(-1) \rho_{2}+\rho_{1}$, $\rho_{1}+\rho_{2}$, $( -1) \rho_{1}$. Bu hamlelerden en sonuncusu dışındakiler determinantı değiştirmiyor; sonuncusu ise determinantın işaretini değiştiriyor. Bu da tam olarak bizim istediğimiz sonucu veriyor. Herhangi iki satırın yerlerinin değiştirildiği durum için de çok benzer bir kanıt yazılabilir.
Eğer $A$ matrisinin iki satırı aynıysa, bu satırların yerini değiştirmekle, $A$ matrisinin kendisi elde edilir. Bir önceki paragraftan dolayı $\operatorname{det} A =-\operatorname{det} A $ olmalı. Bu da $\operatorname{det} A=0 $ demek.
Eğer bir matrisin bir satırı tamamen $0$ ise bu satıra kendisi dışında herhangi bir satıra ekleyerek -determinantı değiştirmeden- iki satırı aynı olan bir matris elde ederiz. Bu durumda da az önce kanıtladığımız önermeden dolayı determinantın $0$ olduğu ortaya çıkar.
Kare bir matrisin tekil olmaması, indirgenmiş eşelon forma getirildiğinde $I_n$ elde edilmesi demektir. O halde eğer verilen bir matris tekil değilse determinantı $I_n$’in determinantının sıfır olmayan bir katı olacak, yani $0$ olamaz. Tersine eğer tekilse eşelon forma dönüştürdüğümüzde tamamıyla $0$ olan bir satır elde edilir ve yüzden de determinantı $0$ olur. $\quad \square$
Önsav 2. Eşelon formdaki bir matrisin determinantı köşegen girdilerinin çarpımıdır.
Kanıt: Eşelon formda bir $A$ matrisi alalım ve bu matrisi $$\begin{pmatrix} a_{11} & a_{12} & a_{13} & \dots & a_{1,n-1} & a_{1n} \\ 0 & a_{22} & a_{23} & \dots & a_{2,n-1} & a_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \dots & a_{n-1,n-1} & a_{n-1,n} \\ 0 & 0 & 0 & \dots & 0 & a_{nn} \\ \end{pmatrix}$$ olarak yazalım. Eğer $A$ tekilse $a_{nn}=0$ olur. Bu durumda da $\operatorname{det} A =0$ yani köşegen girdilerinin çarpımı olur. O halde $A$’nın tekil olmadığını, yani her $i$ için $a_{ii} \neq 0$ olduğunu varsayabiliriz. Şimdi her $i$ için bu matrisin $i$’inci satırını $1/a_{ii}$ ile çarpıp, köşegen girdileri $1$ olan bir matris elde edelim. Bu yeni matrisin determinantı $\frac {1}{a_{11}a_{22}\cdots a_{nn}}\operatorname{det} A$ olur. Yani eğer bu matrisin determinantının $1$ olduğunu gösterirsek kanıtı bitiririz. Bu matrisin köşegeninin üstündeki girdilerini sadece bir satırın bir skaler katını başka bir satıra ekleme hamlesini kullanarak $0$ yapabiliriz. Bu hamleler, determinantı değiştirmez ve sonunda birim matrisi elde ederiz. Yani gerçekten de determinantı $1$ olur. $\quad \square$
Bu önsavı kullanarak, en çok bir determinant fonksiyonu olduğu sonucu çıkartabiliriz. Verilen bir matrisi Gauss hamlelerini kullanarak eşelon forma dönüştürebiliriz; elde ettiğimiz eşelon formdaki matrisin her determinant fonksiyonu altındaki değeri köşegen girdilerinin çarpımı olur. Sonrasında da yaptığımız Gauss hamlelerini takip ederek verilen matrisin her determinant fonksiyonu altında aynı değeri aldığını görürüz. Bunu ileride kullanmak üzere kaydedelim.
Teorem 1. Her $n>0$ için, Tanım 1’deki özellikleri sağlayan en çok bir fonksiyon vardır.
Tabii ki hala böyle bir fonksiyonun varlığını bilmiyoruz; bunu bir sonraki bölümde kanıtlayacağız.
Küçük boyutlu matrislerin determinantlarını bu yeni kurallara göre bularak, daha önceki kısımlarda verdiğimiz formüllerle aynı sonuçları elde ettiğimizi görelim.
Örnek 4. Şu matrise bakalım: $$A= \begin{pmatrix} -1 & 0 & -2 \\ 3 & 2 & -2 \\ 0 & 1 & -2 \\ \end{pmatrix}.$$ İlk olarak determinantı değiştirmeyen şu hamleleri yapalım: $3\rho_{1} + \rho_{2}$, $-\frac {1}{2}\rho_{2} + \rho_{3}$. Bunun sonucunda elde ettiğimiz eşelon formdaki matris $$\begin{pmatrix} -1 & 0 & -2 \\ 0 & 2 & -8 \\ 0 & 0 & 2 \\ \end{pmatrix}$$ oluyor. Bu matrisin determinantı köşegendeki sayıları çarparak $-4$ olarak bulunur. Arada determinantı değiştiren bir hamle yapmadığımızdan $\operatorname{det} A = -4$ olur.
Bir de $4 \times 4$’lük bir matrisin determinantını bulalım.
Örnek 5. Şu matrise bakalım: $$\begin{pmatrix} 7 & 0 & -7 & 0 \\ 8 & 1 & -5 & -2 \\ 0 & 1 & -3 & 0 \\ 0 & 3 & -6 & -1 \\ \end{pmatrix}.$$ Bu matrise sırasıyla $- \frac {8}{7} \rho_{1} + \rho_{2}$, $- \rho_{2} + \rho_{3}$, $-3 \rho_{2} + \rho_{4}$, $- \frac {5}{2} \rho_{3} + \rho_{4} $ hamlelerini uyguladığımızda $$ \begin{pmatrix} 7 & 0 & -7 & 0 \\ 0 & 1 & 3 & -2 \\ 0 & 0 & -6 & 2 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix}.$$ matrisini elde ederiz. Yani başladığımız matrisin determinantı $0$ olur.
Determinant Fonksiyonunun Varlığı
Yukarıda determinantı, çeşitli özellikleri sağlayan bir fonksiyon olarak tanımladık. Hala o özellikleri sağlayan bir fonksiyonun var olup olmadığını bilmiyoruz. Diyebilirsiniz ki “ama yukarıda satır hamleleri yaparak determinant hesapladık; bu da fonksiyonun varlığını göstermez mi?” Sorun, oradaki hesapların iyi tanımlı olduğunu bilmiyor olmamız; yani bir satır hamleleri silsilesi bir determinant verirken bir başkası başka bir sonuç verebilir. Burada bunun olamayacağını göstereceğiz. Bunu yapmak için determinantı tanımlayan kurallara daha öncekinden farklı bir gözle bakacağız. Aşağıda verilen $V$ vektör uzayı ve $n>0$ için $V^n$ ile, elemanları $v_1, \dots, v_{n} \in V$ olmak üzere $$\begin{pmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \\ \end{pmatrix}$$ şeklinde olan kümeyi göstereceğiz.
Tanım 2. Bir $V$ vektör uzayı, $n>0$ ve $$f : V^n \rightarrow \mathbb{R}$$ fonksiyonu verilsin.
- Eğer her $i \in \{ 1, \dots , n\}$ , $v_{1}, \dots , v_{i-1}, v_{i+1}, \dots , v_{n}, v, w \in V$ ve $r,s \in \mathbb{R}$ için $$f \begin{pmatrix} v_1 \\ \vdots \\ v_{i-1} \\ rv+sw \\ v_{i+1} \\ \vdots \\ v_n \\ \end{pmatrix} = rf \begin{pmatrix} v_1 \\ \vdots \\ v_{i-1} \\ v \\ v_{i+1} \\ \vdots \\ v_n \\ \end{pmatrix} + sf \begin{pmatrix} v_1 \\ \vdots \\ v_{i-1} \\ w \\ v_{i+1} \\ \vdots \\ v_n \\ \end{pmatrix} $$ oluyorsa, $f$’ye çoklu lineer denir.
- Eğer her $i \in \{1, \dots , n-1\}$ ve her $v_1, \dots , v_{i-1}, v, v_{i+2}, \dots , v_{n} \in V $ için $$f \begin{pmatrix} v_1 \\ \vdots \\ v_{i-1} \\ v \\ v \\ v_{i+2} \\ \vdots \\ v_{n} \\ \end{pmatrix}=0$$ oluyorsa, $f$’ye dönüşümlü denir.
Çoklu lineer tanımını şu şekilde düşünebiliriz: Bir koordinat haricindeki bütün girdileri sabitleyerek elde ettiğimiz her $V \rightarrow \mathbb{R}$ fonksiyonu lineerdir.
Şimdi matris uzayı $M_n$’yi $(\mathbb{R}^n)^n$ gibi düşünelim: $(\mathbb{R}^n)^n$’den aldığımız bir eleman, $\mathbb{R}^n$’den sıralı bir şekilde alınmış $n$ tane sütun vektörü demektir. Bu vektörleri sırayı bozmadan yana yana yerleştirerek bir matrisin sütünları olarak görebiliriz. İlk olarak -eğer varsa- $M_n$ üzerindeki determinantın dönüşümlü ve çoklu lineer olduğunu göstereceğiz.
Önerme 1. Tanım 1’deki kurallara uyan her fonksiyon dönüşümlü ve çoklu lineerdir.
Kanıt: Determinantın dönüşümlü olduğu Önsav 1’in ikinci kısmına denktir.
Çoklu lineerliği kontrol etmek için şu iki koşulu kontrol etmek yeterlidir:
- Her $i \in \{1, \dots , n\}$ ve $a_{1}, \dots , a_{i-1}, a_{i+1}, \dots , a_{n}, a, b$ satır vektörleri için $$\operatorname{det} \begin{pmatrix} a_1 \\ \vdots \\ a_{i-1} \\ a+b \\ a_{i+1} \\ \vdots \\ a_n \\ \end{pmatrix}= \operatorname{det} \begin{pmatrix} a_1 \\ \vdots \\ a_{i-1} \\ a \\ a_{i+1} \\ \vdots \\ a_n \\ \end{pmatrix} + \operatorname{det} \begin{pmatrix} a_1 \\ \vdots \\ a_{i-1} \\ b \\ a_{i+1} \\ \vdots \\ a_n \\ \end{pmatrix} $$
- Her $i \in \{1,\dots , n\}$, $a_{1},\dots , a_{i-1}, a_{i+1}, \dots , a_{n}, a$ satır vektörleri ve $r \in \mathbb{R}$ için $$\operatorname{det} \begin{pmatrix} a_1 \\ \vdots \\ a_{i-1} \\ ra \\ a_{i+1} \\ \vdots \\ a_n \\ \end{pmatrix}=r \operatorname{det} \begin{pmatrix} a_1 \\ \vdots \\ a_{i-1} \\ a \\ a_{i+1} \\ \vdots \\ a_n \\ \end{pmatrix}.$$ Bunlardan ikincisi zaten determinant koşullarından biri; yani sadece ilkini kanıtlayacağız.
Kolaylık olsun diye $i=1$ alalım ve $A, B, C$ matrislerini sırasıyla şöyle tanımlayalım: $$A=\begin{pmatrix} a \\ a_2 \\ \vdots \\ a_n \end{pmatrix},\; B=\begin{pmatrix} b \\ a_2 \\ \vdots \\ a_n \end{pmatrix},\; C=\begin{pmatrix} a+b \\ a_2 \\ \vdots \\ a_n \end{pmatrix}$$ Yani amacımız $\operatorname{det}A + \operatorname{det}B = \operatorname{det}C$ olduğunu göstermek.
Eğer $a_{2}, \dots , a_n$ lineer bağımlı ise $A$, $B$, $C$ matrislerinin hiç biri tersinir olmadığından (yani hepsi tekil olduğundan), söz konusu determinantların hepsi $0$. O durumda $a_{2}, \dots , a_n$ vektörlerinin lineer bağımsız olduğunu varsayabiliriz. Bu lineer bağımsız kümenin üstüne bir $c$ satır vektörü ekleyip $\mathbb{R}^n$’nin bir tabanına tamamlayalım ve $$\begin{split} a&=r_{1}c + r_{2}a_{2} + \dots + r_{n}a_{n}, \\ b&=s_{1}c + s_{2}a_{2} + \dots + s_{n}a_{n} \end{split}$$ olarak yazalım.
Öyleyse $C$’nin ilk satırı $$(r_{1}+s_{1})c +(r_{2}+s_{2})a_{2} + \dots + (r_{n}+s_{n})a_n$$ olur.
Şimdi $C$’ye sırasıyla şu Gauss hamleelrini uygulayalım: $$-(r_2 + s_2) \rho_2 + \rho_1, \ -(r_3 + s_3) \rho_3 + \rho_1, \ \ldots, \ -(r_n + s_n) \rho_n + \rho_1$$ Bu hamleler sonucunda determinant değişmez ve şunu elde ederiz: $$\begin{split} \operatorname{det}C = &\operatorname{det} \begin{pmatrix} (r_{1}+s_{1})c \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix} \\ =&(r_{1} + s_{1})\operatorname{det}\begin{pmatrix} c \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix} \\ = &r_{1}\operatorname{det}\begin{pmatrix} c \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix} + s_{1} \operatorname{det}\begin{pmatrix} c \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix} \\ = &\operatorname{det}\begin{pmatrix} r_{1}c \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix} + \operatorname{det}\begin{pmatrix} s_{1}c \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix} \end{split}$$ Son adımda determinantını aldığımız matrislere yukarıda yaptığımıza benzer Gauss hamleleri uygulayarak ilk satırlarının sırasıyla $a$ ve $b$ olmasını sağlayabiliriz. Yani son satırdaki toplam $$\operatorname{det}A + \operatorname{det}B$$ toplamına eşit olduğundan kanıtımız biter. $\quad \square$
Bir sonraki önermemiz yukarıdakinin bir anlamda tersi olacak.
Önerme 2. Eğer $f:(\mathbb{R}^n)^n \rightarrow \mathbb{R}$ dönüşümlü ve çoklu lineerse ve $f(I_{n})=1$ ise $f$ Tanım 1’deki koşulları sağlar.
Kanıt: Tanımdaki ilk koşulun sağlandığını göstermek için bir $A$ matrisi ve $A$ matrisinin ilk satırının $r$ katını ikinci satırına ekleyerek elde edilen $B$ matrisi alalım. Amacımız $f(A)=f(B)$ olduğunu göstermek. Bu matrisleri şu şekilde yazalım: $$A=\begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix}, \; B=\begin{pmatrix} v_1 \\ rv_1 +v_2 \\ \vdots \\ v_n \end{pmatrix}$$ Çoklu lineerlikten dolayı $$f(B)=r f\begin{pmatrix} v_1 \\ v_1 \\ \vdots \\ v_n \end{pmatrix} + f\begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix}$$ olur. Burada sol taraftaki ilk terim dönüşümlülükten dolayı $0$ olur, ikinci terim de $f(A)$ oluyor. yani $f(B)=f(A).$
Determinant tanımındaki ikinci koşul çoklu lineerliğin özel bir hali olduğu için gösterilmesi gereken bir şey yok. Son koşul da zaten $f$’le ilgili varsayımlardan biri. Yani kanıtımız burada biter. $\quad \square$
Bu önermelerden dolayı, birim matriste $1$ değeri alan dönüşümlü ve çoklu lineer bir fonksiyonun varlığını gösterdiğimizde determinantın varlığını göstermiş olacağız.
Teorem 2. Her $n>0$ için $f(I_{n})=1$ olacak şekilde dönüşümlü ve çoklu lineer bir $$f:(\mathbb{R}^n)^n \rightarrow \mathbb{R}$$ fonksiyonu vardır.
Kanıt: Bunu $n$ üzerine tümevarımla kanıtlayacağız. Zaten $n=1, 2, 3$ durumlarında böyle bir fonksiyon olduğunu biliyoruz. Şimdi $n-1$ için öyle bir fonksiyon olduğunu varsayalım ve $n$ için de olduğunu gösterelim. (Bu fonksiyonların her ikisini de $f$ ile göstereceğiz)
Bir $$A= \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \\ \end{pmatrix}$$ matrisi alalım ve keyfi seçilmiş $i,j \in \{1, \dots , n \}$ için $(n-1) \times (n-1)$’lik $A_{ij}$ matrisini şöyle tanımlayalım: $$\begin{pmatrix} a_{11} & \dots & a_{1, j-1} & a_{1, j-1} & \dots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{i-1, 1} & \dots & a_{i-1, j-1} & a_{i-1, j+1} & \dots & a_{i-1, n} \\ a_{i+1, 1} & \dots & a_{i+1, j-1} & a_{i+1, j+1} & \dots & a_{i+1, n} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{n1} & \dots & a_{n, j-1} & a_{n, j+1} & \dots & a_{n, n} \\ \end{pmatrix} $$ (Yani $A$’nın $i$’inci satır ve $j$’inci sütununun silinmiş haline $A_{ij}$ diyoruz.)
Tümevarım hipotezinden dolayı her $i,j$ için $f(A_{ij})$ tanımlıdır. Şimdi bir $j$ sabitleyelim ve $f(A_{ij})$’leri kullanarak $f(A)$’yı şöyle tanımlayalım: $$f(A) = \sum_{i=1}^n (-1)^{i+j} a_{ij}f(A_{ij})$$ Yapmamız gereken böyle tanımlanan bir fonksiyonun dönüşümlü ve çoklu lineer olduğunu ve $f(I_{n})=1$ olduğunu göstermek.
İlk olarak dönüşümlü olduğunu gösterelim. Diyelim ki $k<l$ için $k$’inci ve $l$’inci satırlar aynı olsun ve $f(A)$’yı yukarıdaki gibi $j$ sütununa göre hesaplayalım. Bu durumda $k$ ve $l$’den farklı her $i$ için $A_{ij}$’nin iki satırı birbirine eşit olur ve tümevarım hipotezinden dolayı, bu $f(A_{ij})$’ler $0$ olur. Geriye sadece iki tane terim kaldı; onlar da $(-1)^{k+j}a_{kj}f(A_{kj})$ ve $(-1)^{l+j}a_{lj}f(A_{LJ}).$ Burada $a_{kj} = a_{lj}$ olduğuna dikkat edelim. Eğer $A_{kj}$ ve $A_{lj}$ matrislerine dikkatlice bakarsak görürüz ki $l-k-1$ satır değiştirme işlemi yaparsak $A_{lj}$’yi $A_{kj}$’ye dönüştürebiliriz. Yani $$f(A_{lj}) = (-1)^{k-l-1}f(A_{kj}).$$ Yani geriye kalan iki terim birbirlerinin ters işaretlisi olduğundan toplamları $0$ oluyor. Buradan tanımladığımız fonksiyonların dönüşümlü olduğunu görürüz.
Çoklu lineerliği kontrol etmek için şöyle bir matrise bakalım: $$A= \begin{pmatrix} a+b \\ a_2 \\ \vdots \\ a_n \\ \end{pmatrix}$$ (Burada yine kolaylık olsun diye ilk satıra göre lineerliğe bakıyoruz ama genel kanıt burada yapacağımızdan daha zor değil, sadece notasyon daha karmaşık.) $f$’yi tanımlayan formülde, $i \neq 1$ olduğu sürece $A_{ij}$’nin ilk satırı $a + b$ vektörünün $j$’inci dışındaki girdilerinden oluşan satır vektörü olacak ve yine tümevarımla $f(A_{ij})$ ilk satırı $a$ ve ilk satırı $b$ olan iki matrisin determinantlarının toplamı olarak yazılabilecek. Geriye kalan $i=1$ durumunda ise ele aldığımız terim $(-1)^{1+j}(a_{1j}+b_{1j})f(A_{1j})$ oluyor ve bu terimi de $(-1)^{1+j}a_{1j}f(A_{1j})$ ve $(-1)^{1+j}b_{1j}f(A_{1j})$ terimlerinin toplamı olarak yazarsak $$f(A) = f\begin{pmatrix} a \\ a_2 \\ \vdots \\ a_n \end{pmatrix} + f\begin{pmatrix} b \\ a_2 \\ \vdots \\ a_n \end{pmatrix} $$ olduğunu görürüz. $$f(A)=f\begin{pmatrix} ra \\ a_2 \\ \vdots \\ a_n \end{pmatrix}=rf\begin{pmatrix} a \\ a_2 \\ \vdots \\ a_n \end{pmatrix}$$
olduğu da benzer biçimde gösterilebilir.
Son olarak da birim matrisin determinantinin $1$ olduğunu gösterelim. Bu noktada $i=j$ dışındaki bütün $A_{i j}$’lerin $j$’inci satırının tamamen $0$ olduğuna dikkat edelim. Yani o durumlarda $f\left(A_{i j}\right)=0$. Şimdi de $i=j$ durumuna bakarsak $A_{j j}$’nin $(n-1) \times(n-1)$’lik birim matris olduğunu görürüz. Yani $$ f\left(I_{n}\right)=(-1)^{j+j} 1 f\left(I_{n-1}\right)=1\qquad \square$$
Sonunda determinantın varlığını biliyoruz:
Sonuç 1. Her $n>0$ için bir determinant fonksiyonu vardır.
Yukarıda yaptığımız her şeyi satırlar yerine sütunlarla yapabilirdik yani determinantı Gauss hamleleriyle nasıl değiştiğine ilişkin koşullarla değil, sütun hamlelerine göre nasıl değiştiğiyle ilgili koşullarla tanımlayabilirdik. O durumda da determinantin varlığını bir önceki teoremin kanıtında olduğu gibi bir $j$ sütununa göre değil, bir $i$ satırına göre açılım yaparak gösterirdik. Tabii ki bu elde ettiğimiz yeni sonucun da determinantın koşullarını sağlayacağını göstermek gerekli ama o da kolayca yapılabilir. Yani determinantın tekliğinden dolayı sütun hamleleriyle de aynı determinantı elde etmiş oluruz. Bu şekilde determinantları hesaplamak için yeni bir yolumuz oluyor. Ancak daha önemlisi matrislerin devrikleriyle aynı determinanta sahip olduğu sonucu da çıkıyor.
Sonuç 2. Her kare $A$ matrisi için $\operatorname{det} A=\operatorname{det} A^{t}$ olur.
Şuna da dikkat edelim: Bir kez daha determinantın tek olmasından ve yukarıdaki sonuçtan dolayı bir matrisin determinantını, istediğimiz satır ya da sütuna göre hesaplayabiliriz.
Cramer Kuralı
Şimdi determinantın varlığını da bildiğimize göre determinant hakkında daha detaylı özellikler kanıtlayabiliriz. Bunlardan ilki, lineer denklem sistemlerinin çözümlerini bulmaya yarayan Cramer Kuralı.
Teorem 3. Sütunları lineer bağımsız $v_{1},\dots , v_n$ vektörleri olan bir $A$ matrisi verilsin. Her $v \in \mathbb{R}^{n}$ vektörünün $\{v_{1}, \ldots, v_{n}\}$ tabanına göre $j$’inci koordinatı $$ \frac{\operatorname{det}\left(v_{1}, \ldots, v_{j-1}, v, v_{j+1}, \ldots, v_{n}\right)}{\operatorname{det} A}
$$ olur. (Yani $A$’nın $j$’inci sütunu yerine $v$ koyarak elde ettiğimiz matrisin determinantı ile $A$’nın determinantının oranı.)
Kanıt: Verilen $v \in \mathbb{R}^{n}$ vektörünü $\{v_{1}, \ldots, v_{n}\}$ tabanında yazalım: $$ v=x_{1} v_{1}+\cdots+x_{n} v_{n}$$ ve $\operatorname{det}\left(v_{1}, \ldots, v_{j-1}, v, v_{j+1}, \ldots, v_{n}\right) $ determinantına bakalım: $$\begin{split} \operatorname{det}(v_{1}, \ldots, v_{j-1}, v, v_{j+1}, \ldots, v_{n}) &=\operatorname{det}(v_{1}, \ldots, v_{j-1}, x_{1} v_{1}+\cdots+x_{n} v_{n}, v_{j+1}, \ldots, v_{n}) \\ &= x_{1} \operatorname{det}(v_{1}, \ldots, v_{j-1}, v_{1}, v_{j+1}, \ldots, v_{n}) \\ &+\dots \\ &+x_{j} \operatorname{det}(v_{1}, \ldots, v_{j-1}, v_{j}, v_{j+1}, \ldots, v_{n}) \\ &+ \dots \\ &+ \operatorname{det}(v_{1}, \ldots, v_{j-1}, v_{n}, v_{j+1}, \ldots, v_{n}) \end{split}$$ Burada $j$’inci dışında determinantını aldığımız bütün matrislerin iki sütunu aynı; yani sadece $j$’incisi $0$’dan farklıdır. Bu durumda da $\operatorname{det}(v_{1}, \ldots, v_{j-1}, v, v_{j+1}, \ldots, v_{n})$ determinantı $$ x_{j} \operatorname{det}\left(v_{1}, \ldots, v_{j-1}, v_{j}, v_{j+1}, \ldots, v_{n}\right)$$ determinantına yani $x_{j} \operatorname{det} A$ ya eşittir. Şimdi $\operatorname{det} A \neq 0$ olduğundan tam da istediğimiz gibi $$ x_{j}=\frac{\operatorname{det}\left(v_{1}, \ldots, v_{j-1}, v, v_{j+1}, \ldots, v_{n}\right)}{\operatorname{det} A}$$ olur. $\quad \square$
Bu kuralı kullanarak lineer denklem sistemlerini çözebiliriz.
Örnek 6. Şu lineer sisteme bakalım: $$\begin{split} 7x_{3} &= 14 \\ 4x_{1}+\frac{1}{2}x_{2}-x_{3} &= 7 \\ x_{1}-x_{2}+3x_{3} &= 5. \\ \end{split}$$ Cramer kuralını şu vektörlere uygulayalım: $$ v_{1}= \begin{pmatrix} 0 \\ 4 \\ 1 \end{pmatrix},\quad v_{2} = \begin{pmatrix} 0 \\ 1/2 \\ -1 \end{pmatrix},\quad v_{3} = \begin{pmatrix} 7 \\ -1 \\ 3 \end{pmatrix},\quad v= \begin{pmatrix} 14 \\ 7 \\ 5 \end{pmatrix}. $$
Bu durumda Cramer kuralına göre $$ \begin{split} x_{1}=\frac{\operatorname{det} \begin{pmatrix} 14 & 0 & 7 \\
7 & 1 / 2 & -1 \\
5 & -1 & 3
\end{pmatrix}}{\operatorname{det}\begin{pmatrix}
0 & 0 & 7 \\
4 & 1 / 2 & -1 \\
1 & -1 & 3
\end{pmatrix}}, \quad
x_{2}=\frac{\operatorname{det}\begin{pmatrix}
0 & 14 & 7 \\
4 & 7 & -1 \\
1 & 5 & 3
\end{pmatrix}}{\operatorname{det}\begin{pmatrix}
0 & 0 & 7 \\
4 & 1 / 2 & -1 \\
1 & -1 & 3
\end{pmatrix}}, \quad
x_{3}=\frac{\operatorname{det}\begin{pmatrix}
0 & 0 & 14 \\
4 & 1 / 2 & 7 \\
1 & -1 & 5
\end{pmatrix}}{\operatorname{det}\begin{pmatrix}
0 & 0 & 7 \\
4 & 1 / 2 & -1 \\
1 & -1 & 3
\end{pmatrix}}
\end{split}
$$
olur. Bu determinantları hesapladığımızda
$$
x_{1}=\frac{17}{9}, \quad x_{2}=\frac{26}{9}, \quad x_{3}=2
$$
elde edilir.
Determinant Hesaplamanın Bir Yolu Daha: Dizilim Açılımı
İki küme arasındaki birebir ve örten fonksiyonlara eşleme denildiğini hatırlayalım. Burada $n$ elemanlı bir kümeden kendisine giden eşlemelere de dizilim diyeceğiz. Daha titiz bir tanım şöyle:
Tanım 3. Eğer bir $$\sigma:\{1, \ldots, n\} \rightarrow\{1, \ldots, n\}$$ fonksiyonu eşlemeyse, bu fonksiyona $n$’nin bir dizilimi diyeceğiz. Bir $\sigma$ dizilimini çoğu zaman $(\sigma(1), \ldots, \sigma(n))$ olarak göstereceğiz. Verilen bir $n>0$ için $n$ ‘nin bütün dizilimlerinin kümesini $\Sigma_{n}$ ile göstereceğiz.
Örnek 7. İlk olarak $n=2$ durumuna bakalım. Bu durumda $1$ nereye giderse, $2$ de geriye kalan elemana gidecek. Yani sadece iki tane dizilim var. Bir tanesi birim dizilim: $(1,2)$; diğeri de $(2,1)$ dizilimi.
Örnek 8. Şimdi de $n=3$ durumuna bakalım. Burada daha fazla dizilim var. Bunları şöyle listeleyelim:
$$
\begin{split}
& \sigma_{1}=(1,2,3),\; \sigma_{2}=(1,3,2),\; \sigma_{3}=(2,1,3), \\
& \sigma_{4}=(2,3,1),\; \sigma_{5}=(3,1,2),\; \sigma_{6}=(3,2,1) .
\end{split}
$$
Bizim dizilimlerle ilgilenmemizin sebebi, bu dizilimleri standart tabanın elemanlarına uygulayarak -girdileri sadece $0$ ve $1$ olan- yeni matrisler elde ettikten sonra bunları kullanarak yeni bir determinant formülü bulmak.
Tanım 4. Verilen bir $\sigma=(\sigma(1), \ldots, \sigma(n))$ dizilimi için $I_{\sigma}$ matrisi $i$ ‘inci sütunu $e_{\sigma(i)}$ olan matristir.
Mesela, birim dizilime denk gelen matris birim matristir. Yukarıdaki örnekteki $\sigma_{4}$ dizilimine denk gelen matris de şudur:
$$
I_{\sigma_{4}}=\begin{pmatrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
\end{pmatrix}.
$$
Bu yeni notasyonu kullanarak verilen bir matrisin determinantını şu şekilde hesaplayabiliriz.
Teorem 4. Verilen $n \times n$’lik bir $A=\left(a_{i j}\right)_{i, j}$ matrisinin determinantı şu formülle hesaplanabilir:
$$
\operatorname{det} A=\sum_{\sigma \in \Sigma_{n}} a_{1 \sigma(1)} a_{2 \sigma(2)} \cdots a_{n \sigma(n)} \operatorname{det} I_{\sigma} .
$$
Bu teoremin kanıtı oldukça teknik olduğu için burada ayrıntılı olarak yazmayacağız, ama aşağıda $n=2$ durumunda yapacağımız hesap genel kanıt hakkında fikir verecektir diye düşünüyoruz.
Bir $2 \times 2$’lik matris alalım:
$$ A=\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{pmatrix} $$
Determinantın çoklu lineer olduğunu kullanan şu adımlara bakalım:
$$ \begin{aligned} \operatorname{det}\left(\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right) & = \operatorname{det}\left(\begin{array}{rr} a_{11} & 0 \\ a_{21} & a_{22} \end{array}\right) + \operatorname{det}\left(\begin{array}{rr} 0 & a_{12} \\ a_{21} & a_{22} \end{array}\right) \\
&= a_{11} \operatorname{det}\left(\begin{array}{rr} 1 & 0 \\ a_{21} & a_{22} \end{array}\right) + a_{12} \operatorname{det}\left(\begin{array}{rr} 0 & 1 \\ a_{21} & a_{22} \end{array}\right) \\
&= a_{11}\left( a_{21} \operatorname{det}\left(\begin{array}{rr} 1 & 0 \\ 1 & 0 \end{array}\right) + a_{22} \operatorname{det}\left(\begin{array}{rr} 1 & 0 \\ 0 & 1 \end{array}\right)\right) + a_{12}\left(a_{21} \operatorname{det}\left(\begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array}\right) + a_{22} \operatorname{det}\left(\begin{array}{rr} 0 & 1 \\ 0 & 1 \end{array}\right)\right) \\
&= a_{11} a_{22} \operatorname{det}\left(\begin{array}{rr} 1 & 0 \\ 0 & 1 \end{array}\right) + a_{12} a_{21} \operatorname{det}\left(\begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array}\right) \\ &= a_{11} a_{22} \operatorname{det} I_{(12)} + a_{12} a_{21} \operatorname{det} I_{(21)}. \end{aligned} $$
Son satırdaki işlemin tam olarak iddia ettiğimiz formül olduğuna ve bu işleminin sonucunun da $a_{11} a_{22}-a_{12} a_{21}$, yani $\operatorname{det} A$ olduğuna da dikkat edelim.
Dizilim açılımını kullanmaya yatkınlık elde etmeniz için size eğlenceli bir alıştırma ekliyoruz.
Alıştırma 1. Her $n>0$ için $A_{n}$ aşağıdaki $n \times n$’lik matris olsun:
$$
\left( \begin{array}{cccccccc} 1 & i & 0 & 0 & \cdots & \cdots & 0 & 0 \\ i & 1 & i & 0 & \cdots & \cdots & 0 & 0 \\ 0 & i & 1 & i & \ddots & & \vdots & \vdots \\ 0 & 0 & i & 1 & \ddots & \ddots & 0 & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & i & 0 & 0 \\ 0 & 0 & & \ddots & i & 1 & i & 0 \\ 0 & 0 & \cdots & \cdots & 0 & i & 1 & i \\ 0 & 0 & \cdots & \cdots & 0 & 0 & i & 1 \end{array} \right)
$$
Yani bu matrisin köşegenindeki girdileri $1$, köşegenin bir altındaki ve bir üstündeki girdileri $i$, geriye kalan girdileriyse $0.$ (Burada $i^{2}=-1$ olduğunu da hatırlayalım.)
Buna göre genel terimi $a_{n}=\operatorname{det} A_{n}$ şeklinde tanımlanan dizi hangi dizidir?
Çarpımın Determinantı
Amacımız, verilen $n \times n$’lik iki matrisin çarpımının determinantının, determinantlarının çarpımıyla aynı olduğunu göstermek. Bunu ilk matrisi sonlu tane elementer matrisin çarpımı olarak yazarak yapacağız. Şu önsavla başlayalım.
Önsav 3. Eğer $T$ elementer bir matris ve $S$ herhangi bir matris ise $\operatorname{det}(T S)=\operatorname{det} T \operatorname{det} S$ olur.
Kanıt: $T$ matrisi için olası seçeneklerin şunlar olduğunu hatırlayalım:
$$
M_{i}(r), \quad P_{i j}, \quad C_{i, j}(r) .
$$
Eğer $T$, bir $r \neq 0$ için bunlardan ilkiyse o zaman $T S$ matrisi $S$’nin $i$’inci satırının $r$ ile çarpılmasıyla elde edilen matris olur. Yani
$$
\operatorname{det}(T S)=r \operatorname{det} S=\operatorname{det} T \operatorname{det} S .
$$
Benzer biçimde eğer $T$, birim matrisin $i$’inci ve $j$’inci satırları yer değiştirilerek elde edildiyse $T S$, $S$’nin $i$’inci ve $j$’inci satırları yer değiştirilerek elde edilir ve yine
$$
\operatorname{det}(T S)=-\operatorname{det} S=\operatorname{det} T \operatorname{det} S
$$
olur. Son durumdaysa $T$ ile çarpmak $S$’nin determinantının değerini değiştirmez ve yine aradığımız çarpımsallık özelliğini elde ederiz. $\quad \square$
Şimdi asıl amacımız olan sonucu kanıtlamaya hazırız.
Teorem 5. Verilen $n \times n$’lik $A$ ve $B$ matrisleri için $\operatorname{det}(A B)=\operatorname{det} A \operatorname{det} B$ olur.
Kanıt: İlk olarak $A$’nın tersinir olmadığı duruma bakalım. Bu durumda $\operatorname{det} A=0$ olacağı için $A B$ matrisinin de tersinir olmadığını göstermek gerekli. Diyelim ki $A B$’nin bir tersi olsun; tersine $C$ diyelim. Bu durumda $(A B) C=I_{n}$ olur. Ama bu $A(B C)=I_{n}$ olduğunu, yani $A$’nın da tersi olduğunu gösteriyor.
Bu durumda kanıtın geri kalanında $A$’nın tersinir olduğunu varsayacağız. O halde $A=T_{1} T_{2} \cdots T_{m}$ olacak şekilde $T_{1}, \ldots, T_{m}$ elementer matrisleri vardır.
Şimdi
$$\begin{aligned}
\operatorname{det}(A B) & =\operatorname{det}\left(T_{1} T_{2} \cdots T_{m} B\right) \\
& =\operatorname{det} T_{1} \operatorname{det}\left(T_{2} \cdots T_{m} B\right) \\
& =\operatorname{det} T_{1} \operatorname{det} T_{2} \cdots \operatorname{det} T_{m} \operatorname{det} B \\
& =\operatorname{det}\left(T_{1} T_{2} \cdots T_{m}\right) \operatorname{det} B \\
& =\operatorname{det} A \operatorname{det} B
\end{aligned}$$
olduğundan kanıtımız biter. $\quad \square$
Determinantın Geometrik Anlamı
Henüz bir vektör uzayında açı, uzunluk ve alan gibi kavramları tanımlamadık. Bunları daha sonra, iç çarpım uzayı kavramıyla birlikte inceleyeceğiz. Ancak determinantın geometrik anlamını incelemeyi de daha fazla ertelemek istemiyoruz. Bunun için $\mathbb{R}^{2}$ örneğinde bu kavramları şimdilik tanımlı kabul edeceğiz. Bu kabul için $\mathbb{R}^{2}$’yi hem bir vektör uzayı hem de bildiğimiz analitik düzlem olarak görmemiz yeterli. Böylece bir vektörün uzunluğundan veya iki vektör arasındaki açıdan söz edebiliriz.
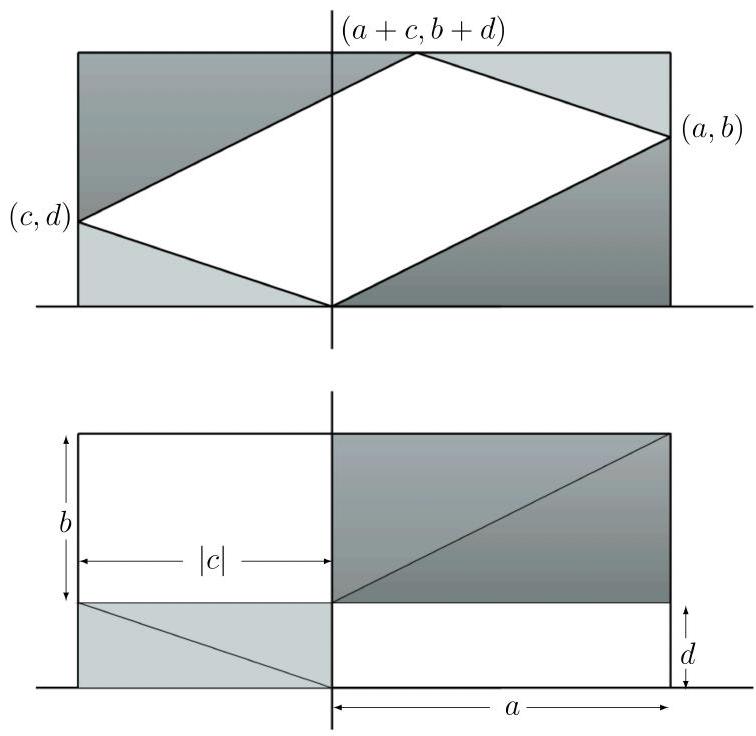
Analitik düzlemin birinci bölgesinde $(a, b)$ ve $(c, d)$ vektörleri verilsin. Bu iki vektör bir paralelkenar belirler. Vektörlerin toplamı olan vektör bu paralelkenarın köşegenidir. Paralelkenarın köşeleriyse $(0,0)$, $(a, b)$, $(a+c, b+d)$ ve $(c, d)$ noktalarındadır. Amacımız bu paralelkenarın alanını verecek bir determinant bulmak.

Önce paralelkenarın sağ üst köşesinden eksenlere dik inerek bir dikdörtgen oluşturalım. Sonra paralelkenarın diğer köşelerinden de oluşturduğumuz bu dikdörtgene aşağıdaki gibi dikler indirelim. Böylece büyük dikdörtgenin içinde başladığımız paralelkenar dışında dört üçgen ve iki dikdörtgen daha oluştu.
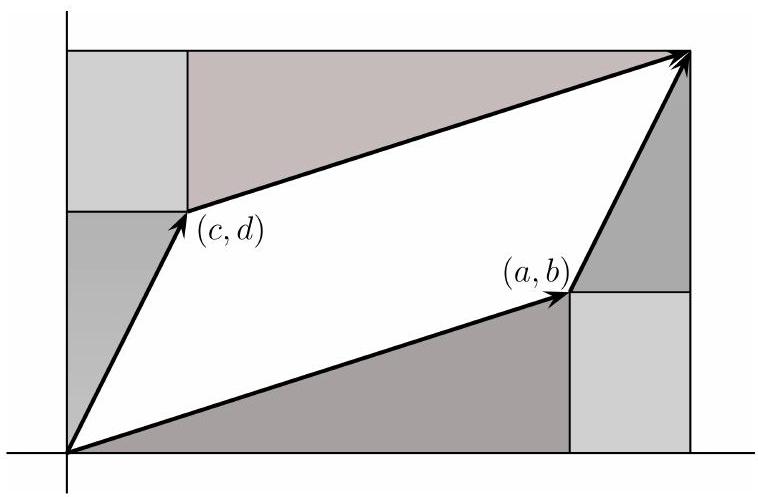
Parelelkenarın birbirine paralel kenarlarına yapışık üçgenlerin, karşılıklı olarak eş üçgenler olduğu ve köşelerdeki diktörtgenlerin eş dikdörtgenler olduğu kolayca gösterilebilir. Dolayısıyla bu üçgenleri hipotenüsleri boyunca birbirlerine yapıştırarak aşağıdaki durumu elde edebiliriz.
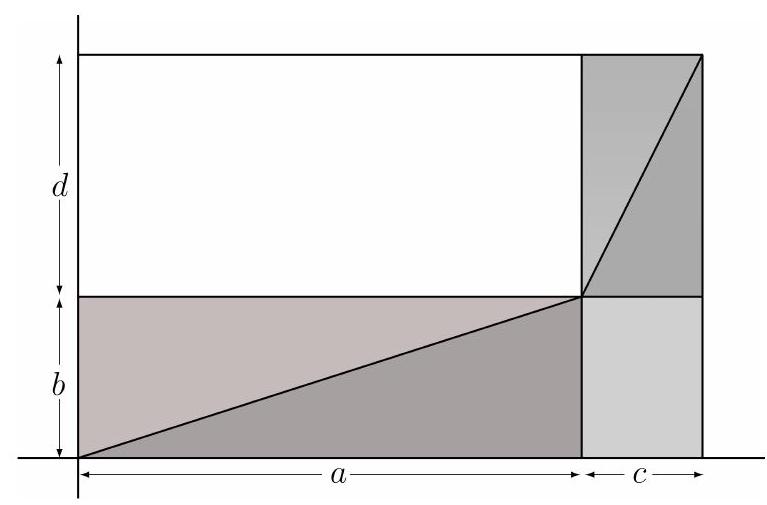
Yukarıdaki her iki figürde de bulunan dört üçgenle bir dikdörtgen, her iki şekilde de aynı alanı kapladığından bunları unutup
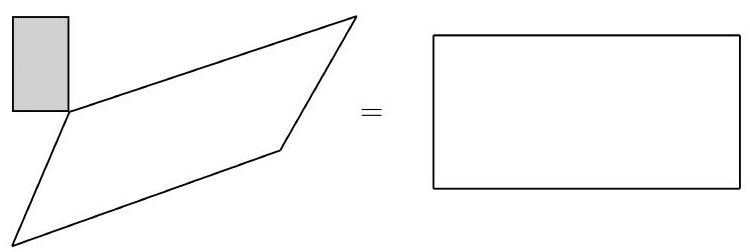
eşitliğine ulaşırız. Böylece paralelkenarın alanını
$$
a d-b c
$$
veya
$$
\operatorname{det}\left(\begin{array}{cc}
a & c \\
b & d \\
\end{array}\right)
$$
olarak yazabiliriz. Ancak iki vektörün oluşturduğu paralelkenarın alanını determinantla hesaplamak istediğimizde dikkat etmemiz gereken bazı noktalar var. Öncelikle yukarıda $(a, b)$ ile $(c, d)$ vektörleri, determinantını aldığımız matrisin sırasıyla birinci ve ikinci sütunlarına yazıldılar. Bunların yerlerini değiştirdiğimizde determinantın negatif olacağını biliyoruz. Yani vektörleri hangi sırayla yazacağımızı bilmiyorsak alanı bulmak için determinantın mutlak değerine bakmalıyız. Öte yandan sırayı yanlış yazdığımızda determinantın negatif çıkması determinantın sadece alan hakkında değil aynı zamanda vektörlerin düzlemde saat yönünde mi ters saat yönünde mi sıralandıkları hakkında da bilgi taşıdığını gösteriyor.
Ayrıca yukarıda incelediğimiz durum analitik düzlemin birinci bölgesindeki vektörler için geçerli. Eğer iki vektör arasındaki açı bir dar açıysa, vektörlerin arasındaki açıyı bozmadan, her ikisini birden döndürerek onları birinci bölgeye taşıyabiliriz. (İki vektörün arasındaki açıyla oluşturdukları iki açıdan küçük (eşit) olanı kastdediyoruz.) Bu döndürme sırasında paralelkenarın alanı değişmeyeceğinden yukarıdaki inceleme geçerlidir.
Geriye aralarındaki açı bir geniş açı olan vektörler kaldı. Bu durumda da aralarındaki açı iki dik açıdan küçük veya iki dik açıya eşit olacaktır. İki dik açıdan küçük olduğu durumu aşağıdaki şekilleri inceleyerek açıklamayı bir alıştırma olarak birakıyoruz.
Son olarak iki vektörün arasındaki açının sıfır veya iki dik açıya eşit olduğu durumla bir dik açı olduğu durumları da göz önünde bulundurmalıyız. Eğer vektörler arasındaki açı sıfırsa veya iki dik açıya eşitse, vektörler bir paralelkenar oluşturamazlar. Vektörleri sütunlarına yazdığımız matrisin determinantı da, sütunlardan biri diğerinin bir skaler katı olduğundan sıfırdır. Eğer vektörler arasındaki açı, bir dik açıysa vektörlerin birinci bölgede olduklarını hatırlayarak karşılık gelen matrisin bir köşegen matris olacağını söyleyebiliriz. Yani $b=c=0$ ve determinant, $a d$ çarpımına eşit olur.
Yukarıda $\mathbb{R}^{2}$ için yaptığımız bu inceleme daha büyük boyutlarda da düzgün geometrik şekillerin hacimlerini determinantı kullanarak bulabileceğimizi düşündürüyor. Bu sezgimizi düzgün geometrik şekil ifadesiyle ne kastettiğimizi tanımlayarak somutlaştıralım. Sonra da yine sezgimize uygun olarak bu şekillerin hacimlerini birer determinant olarak tanımlayalım. İleride sezgimizin doğru sonuç verdiğini göreceğiz.
Tanım 5. Verilen $v_{1}, \ldots, v_{n} \in \mathbb{R}^{n}$ ile belirlenen paralelyüzlü şu kümedir:
$$
\{r_{1} v_{1}+\cdots+r_{n} v_{n}:\, r_{1}, \ldots, r_{n} \in[0,1]\} .
$$
Bu paralelyüzlünün hacmi, $\left|\operatorname{det}\left(v_{1} v_{2} \cdots v_{n}\right)\right|$ olarak tanımlanır.
Bu tanımların sezgimize niçin uygun olduğunu daha iyi görmek için okurumuzu aşağıdaki şekli inceleyerek $n=3$ durumunda hacim determinant ilişkisini geometrik olarak kurmaya davet ediyoruz.
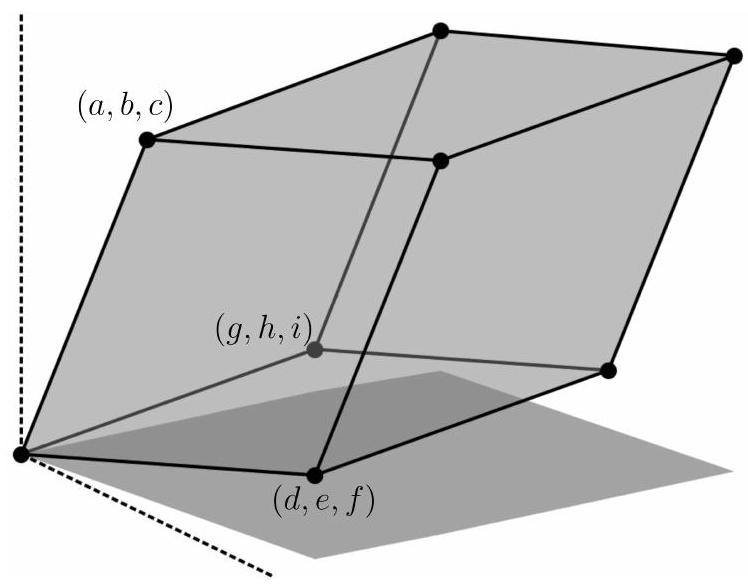
Ayrıca okurumuz $\mathbb{R}^{2}$ için yaptığımız incelemeler ile ulaştığımız diğer sonuçların daha büyük boyutlarda ne anlama geldiğini de düşünmeli. Örneğin, $\mathbb{R}^{2}$’de olduğu gibi bu tanımımıza göre de eğer $v_{1}, \ldots, v_{n}$ lineer bağımlıysa, bu vektörlerle belirlenen paralelyüzlünün hacmi yine $0$ olur mu? $\mathbb{R}^{2}$’de lineer bağımlı iki vektörle verilen paralelyüzlünün hacminin $0$ olmasının nedeni bu iki vektörün sadece bir doğru parçası vermesiydi. Yani bu iki vektör bir hacim ya da alan belirlemiyordu. $\mathbb{R}^{3}$’te hangi durumlar oluşabilir? Determinant hangi durumlarda negatif çıkar? Yani vektörleri satırlara hangi sırayla yazmalıyız ki, determinant mutlak değer almaya gerek olmadan hacmi versin?
Şimdi $\mathbb{R}^{2}$ incelememizdeki bir noktaya geri dönelim: “Eğer iki vektör arasındaki açı bir dar açıysa, vektörlerin arasındaki açıyı bozmadan, her ikisini birden döndürerek onları birinci bölgeye taşıyabiliriz.” demiştik. Bu ifademizi netleştirelim. Her iki vektörü de aynı yönde aynı miktarda döndürebilmek istiyoruz. Aslında vektörlerin başlangıç noktalarını orijin olarak düşünerek her vektörü orijin etrafında aynı yönde aynı miktarda döndüreceğiz. Üstelik bunu bir lineer dönüşümle yapacağız. Yani öyle bir lineer dönüşüm bulacağız ki verilen her vektörü saatin tersi yönünde belirlediğimiz açı kadar döndürecek. Düzlemde bir $(a, b)$ vektörü verilsin. Bu vektörü saatin tersi yönünde bir $\theta$ açısı kadar döndürmek istiyoruz. Döndürme işlemi sonrasında oluşan yeni vektörün koordinatları $\left(a^{\prime}, b^{\prime}\right)$ olsun.
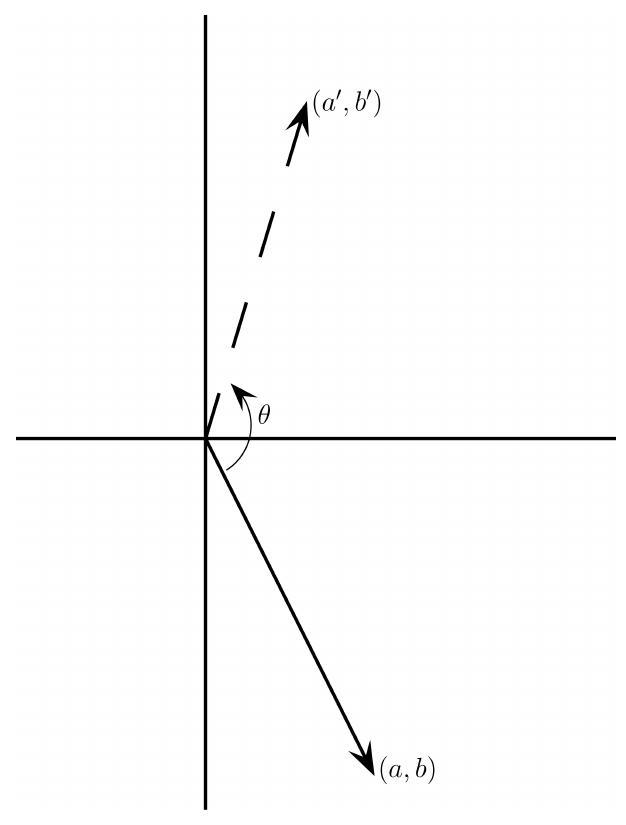
Amacımız $f(a, b)=\left(a^{\prime}, b^{\prime}\right)$ olacak şekilde bir $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ lineer dönüşümü bulmak. Böyle bir dönüşümün var olduğunu kabul edersek
$$f(a, b)=a f(1,0)+b f(0,1)$$
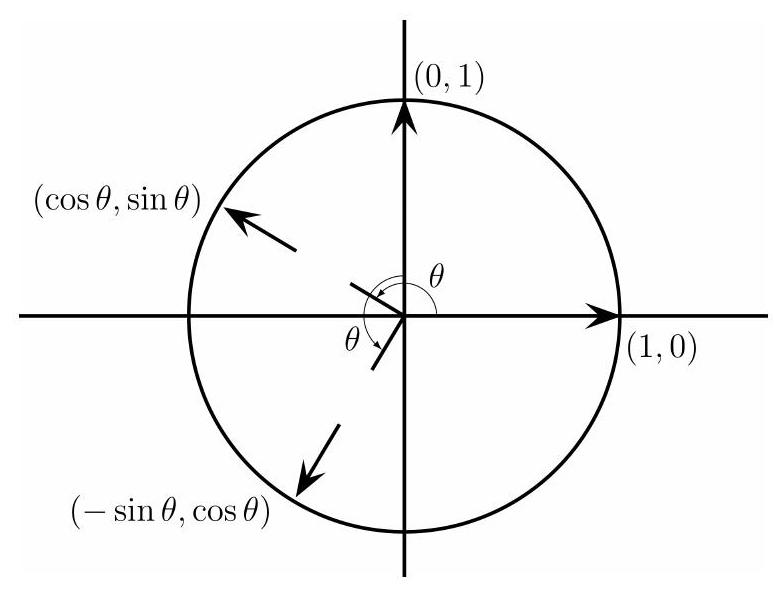
yazabiliriz. Elbette $f$ lineer dönüşümü her vektörü saatin tersi yönünde $\theta$ açısı kadar döndüreceğinden $f(1,0)$ vektörü $(1,0)$ vektörünü saatin tersi yönünde $\theta$ açısı kadar döndürerek bulunabilir. Aynı şekilde, $f(0,1)$ vektörü $(0,1)$ vektörünü saatin tersi yönünde $\theta$ açısı kadar döndürerek bulunabilir. Ama $(1,0)$ vektörünü ters saat yönünde $\theta$ açısı kadar döndürmek birim çember üzerinde $(\cos \theta,\, \sin \theta)$ noktasına gelmek demek. Yani
$$ f(1,0)=(\cos \theta,\, \sin \theta)$$
olmalı. Benzer şekilde $(0,1)$ vektörünü ters saat yönünde $\theta$ açısı kadar döndürmek birim çember üzerinde $\left(\cos \left(\frac{\pi}{2}+\theta\right),\, \sin \left(\frac{\pi}{2}+\theta\right)\right)$ noktasına gelmek demek. Buradan da
$$
f(0,1)=\left(\cos \left(\frac{\pi}{2}+\theta\right),\, \sin \left(\frac{\pi}{2}+\theta\right)\right)
$$
olması gerektiğini buluyoruz. $\cos \left(\frac{\pi}{2}+\theta\right)=-\sin \theta$ ve $\sin \left(\frac{\pi}{2}+\theta\right)=\cos \theta$ özdeşliklerini hatırlayarak bu son ifadeyi
$$
f(0,1)=(-\sin \theta, \cos \theta)
$$
şeklinde yazabiliriz.
Bunları
$$
f(a, b)=a f(1,0)+b f(0,1)
$$
ifadesine yerleştirince
$$
\begin{aligned}
f(a, b) & =a(\cos \theta,\, \sin \theta)+b(-\sin \theta,\, \cos \theta) \\
& =(a \cos \theta-b \sin \theta,\, a \sin \theta+b \cos \theta)
\end{aligned}
$$
olması gerektiğini görüyoruz. Bunun gerçekten de verilen bir vektörü saatin tersi yönünde $\theta$ kadar döndüren bir lineer dönüşüm olduğunu kontrol etmeyi okurumuza bırakıp döndürme işleminin alanı koruduğunu gösterelim.
Önce bu lineer dönüşüme karşlık gelen matrisi yazalım:
$$ M_{f}=\left(\begin{array}{rr}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right) . $$
Eğer başlangıçta verilen $(a, b)$ ve $(c, d)$ vektörleri bu lineer dönüşümle $\theta$ açısı kadar döndürülmüşlerse ve $f(c, d)=\left(c^{\prime}, d^{\prime}\right)$ yazarsak
$$ \begin{aligned}
a^{\prime} & =a \cos \theta-b \sin \theta \\
b^{\prime} & =a \sin \theta+b \cos \theta \\
c^{\prime} & =c \cos \theta-d \sin \theta \\
d^{\prime} & =c \sin \theta+d \cos \theta
\end{aligned}$$
olmak üzere oluşan yeni paralelkenarın alanı
$$
\operatorname{det}\left(\begin{array}{cc}
a^{\prime} & c^{\prime} \\
b^{\prime} & d^{\prime}
\end{array}\right)
$$
şeklinde yazılabilir. Öte yandan,
$$ \left(\begin{array}{rr}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right)\left(\begin{array}{ll}
a & c \\
b & d
\end{array}\right)=\left(\begin{array}{ll}
a^{\prime} & c^{\prime} \\
b^{\prime} & d^{\prime}
\end{array}\right) $$
olduğunu görüyoruz. Ancak
$$ \operatorname{det}\left(\begin{array}{rr}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right)=\cos ^{2} \theta+\sin ^{2} \theta=1 $$
olduğundan
$$\operatorname{det}\left(\begin{array}{cc}
a & c \\
b & d
\end{array}\right)=\operatorname{det}\left(\begin{array}{cc}
a^{\prime} & c^{\prime} \\
b^{\prime} & d^{\prime}
\end{array}\right) $$
sonucuna ulaşırız. Bunun anlamı da döndürme işlemi sonrasında alanın değişmediğidir.
Daha önce kanıtladığımız ‘determinantın çarpımsallığı’ sonucunun burada nasıl kullanıldığına dikkat edelim. Eşitliğin sol tarafında yer alan iki matrisin çarpımının determinantını, önce determinantlarının çarpımıyla değiştirdik. Sonra $\operatorname{det} M_{f}=1$ olduğunu kullandık. Eğer $\left|\operatorname{det} M_{f}\right|=1$ olmasaydı alan değişecekti. Bu durumu sıradaki sonuçta açıklıyoruz.
Sonuç 3. Bir $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ lineer fonksiyonu alalım. Bu fonksiyon paralelyüzlülerin hacimlerini $\left|\operatorname{det} M_{f}\right|$ oranında değiştirir; yani verilen bir $P$ paralelyüzlüsünün hacmi $h$ ise $f(P)$’nin hacmi $\left|\operatorname{det} M_{f}\right| h$’dir.
Kanıt: Diyelim ki $P$ paralelyüzlüsü $v_{1}, \ldots, v_{n}$ vektörleriyle belirleniyor olsun. Bu durumda $f(P)$ paralelyüzlüsü $f\left(v_{1}\right), \ldots, f\left(v_{n}\right)$ vektörleriyle belirlenen paralelyüzlü olur. Yani $f(P)$ ‘nin hacmi şudur
$$ \left|\operatorname{det}\left(M_{f} \cdot\left(v_{1} v_{2} \cdots v_{n}\right)\right)\right|
= \left|\operatorname{det} M_{f}\right|\left|\operatorname{det}\left(v_{1} v_{2} \cdots v_{n}\right)\right| = \left|\operatorname{det} M_{f}\right| h . \quad \square$$
Bu sonuca göre
$$ \left(\begin{array}{ll}
2 & 1 \\
0 & 1
\end{array}\right) $$
matrisiyle verilen $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ lineer dönüşümü, bir köşesi $(0,0)$ noktasında olan bir paralelkenarı, alanı $2$ kat artmış ve yine bir köşesi $(0,0)$ noktasında olan bir paralelkenara götürmeli. Bunu yukarıda döndürme matrisini bulurken kullandığımız yöntemle biraz açalım: Bir$ (a, b)$ vektörü verilsin. Bu durumda
$$ f(a, b)=a\left(\begin{array}{ll}
2 & 1 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
1 \\
0
\end{array}\right)+b\left(\begin{array}{ll}
2 & 1 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
0 \\
1
\end{array}\right) $$
yazarak
$$
f(a, b)=f(a, 0)+f(0, b)=(2 a, 0)+(b, b)
$$
olduğunu görebiliriz. Başka bir şekilde söylersek: $f$ lineer dönüşümü bir $(a, b)$ vektörünün $x$-bileşeninin boyunu $2$ kat artırırken, $y$-bileşenini yana doğru yatırıyor. Böylece bir köşegeni $(0,0)$ ve $(a, b)$ noktaları arasında olan dikdörtgen alanı iki kat artmış bir paralelkenara dönüştü:
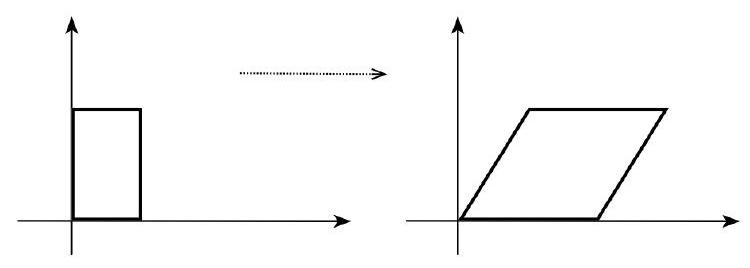
Aslında önce standart taban elemanları $(1,0)$ ve $(0,1)$ tarafindan oluşturulan karenin görüntüsüne bakıp sonra $a$ ve $b$ ile ölçekleyerek yine bu sezgiye ulaşabilirdik:
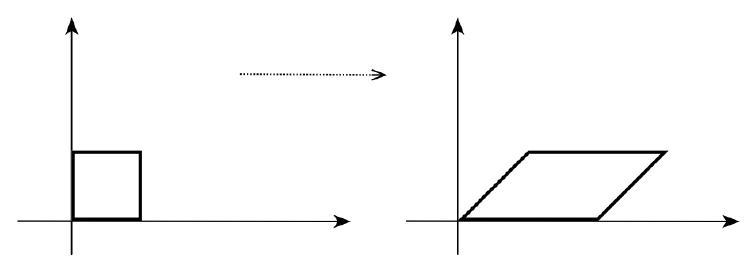
Bu lineer dönüşümün $x$-ekseni yani $y=0$ doğrusu üzerindeki vektörlerin uzunluğunu iki kat artırırken, $y=-x$ doğrusu üzerindeki vektörleri oldukları gibi bıraktığına dikkat edelim. Üstelik bu iki doğru üzerinde kalmayan diğer bütün vektörlerin doğrultularının değiştiğini okurumuz bir alıştırma olarak kontrol etmeli. Bu konuya sıradaki bölümde döneceğiz.
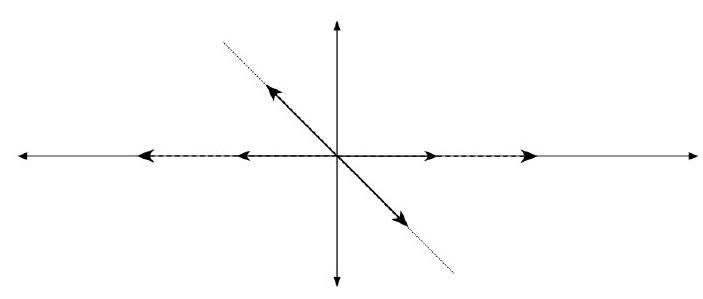
Geometrik sezgimizi de istediğimiz şekilde etki eden lineer dönüşümler bulmak için kullanabiliriz. Örneğin, aşağıdaki çizimden bu şekilde etki eden bir lineer dönüşümün vektörlerin $x$-bileşeninin boyunu $2$ kat azaltırken, $y$-bileşenlerinin boyunu $2$ kat artırması gerektiğini görüyoruz.
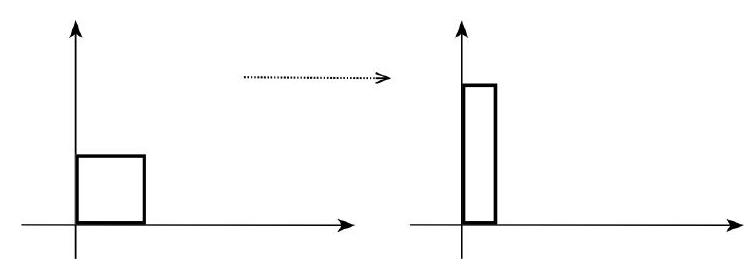
Bunun için $(1,0)$ vektörünün boyunu yarıya indiren ve $(0,1)$’in boyunu iki katına çıkaran
$$ \left(\begin{array}{cc}
1 / 2 & 0 \\
0 & 2
\end{array}\right) $$
matrisiyle verilen lineer dönüşümü kullanabiliriz.
Alıştırma 2. Sonraki sayfada $(1,0)$ ve $(0,1)$ tarafından oluşturulan karenin farklı lineer dönüşümler altındaki görüntülerinin çizimlerini bulacaksınız. Bu lineer dönüşümlere karşılık gelen martrisler neler olabilir?
Bu bölümü tamamlamadan önce döndürme matrisini bulurken harcadığımız emeğin karşılığında bir ödül olarak, zaman zaman hatırlamakta zorlandığımız bazı trigonometrik özdeşlikleri kolayca nasıl üretebileceğimizi görelim.
Düzlemdeki herhangi bir vektörü $\alpha+\beta$ açısı kadar döndürmek ilk önce $\alpha$ sonra $\beta$ kadar döndürmekle aynıdır. Dolayısıyla bu döndürmelere karşılık gelen matrisler arasında şu eşitlik vardir:
$$ \left(\begin{array}{cc}
\cos (\alpha+\beta) & -\sin (\alpha+\beta) \\
\sin (\alpha+\beta) & \cos (\alpha+\beta)
\end{array}\right)
= \left(\begin{array}{cc}
\cos \beta & -\sin \beta \\
\sin \beta & \cos \beta
\end{array}\right)\left(\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right)$$
Çarpımı yapıp düzenleyince
$$ \begin{aligned}
& \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta \\
& \sin (\alpha+\beta)=\cos \alpha \sin \beta+\cos \beta \sin \alpha
\end{aligned} $$
özdeşliklerini elde ederiz.


