$\mathbb{R}^{n}$ uzayındaki vektörleri verilen bir açıyla döndürmenin lineer dönüşüm olduğundan 2014-II’de bahsedip bu dönüşümü detaylı biçimde irdeleşmiştik.
Herhangi bir vektör uzayında açılardan bahsetmek çok mümkün olmasa da diklikten bahsetmek mümkün. Biz de bu bölümde bunu yapacağız. Bunu yapmak için iç çarpım kavramını tanıtmak gerekli.
Bu bölümde daha önceki kısımlarda yaptığımız vektör uzaylarının sonlu boyutlu olduğu varsayımını bırakıyoruz.
İç Çarpım ve Diklik
Daha önce $\mathbb{R}^{n}$’deki iki vektörün iç çarpımından bahsetmiştik. Orada, verilen
$$
a=\left(\begin{array}{c}
a_{1} \\
a_{2} \\
\vdots \\
a_{n}
\end{array}\right) \quad \text { ve } \quad v=\left(\begin{array}{c}
v_{1} \\
v_{2} \\
\vdots \\
v_{n}
\end{array}\right)
$$
vektörleri için
$$
f_{a}(v)=a_{1} v_{1}+a_{2} v_{2}+\cdots+a_{n} v_{n}
$$
tanımını yapmıştık. Burada $f_{a}(v)$ yerine $a \cdot v$ yazacağız. Bu çarpımın şu özelliklerine dikkat edelim:
- Her $v, w \in \mathbb{R}^{n}$, için $v \cdot w=w \cdot v$.
- Her $v, w, u \in \mathbb{R}^{n}$ için
$$
v \cdot(w+u)=(v \cdot w)+(v \cdot u) .
$$
- Her $v, w \in \mathbb{R}^{n}$ ve $r \in \mathbb{R}$ için
$$
r v \cdot w=r(v \cdot w)=v \cdot r w .
$$
- Sıfır olmayan her $v \in \mathbb{R}^{n}$ için $v \cdot v>0$ ve $0_{\mathbb{R}^{n}} \cdot 0_{\mathbb{R}^{n}}=0$.
Bizim buradaki amacımız, bu özellikleri izole edip herhangi bir vektör uzayı üzerinde iç çarpım kavramını tanımlamak. Bunu yaparken aklımızdaki temel örnek yukarıdaki iç çarpım olacak ama notasyonu bir kez daha değiştirip $v \cdot w$ yerine $\langle v, w\rangle$ yazacağız.
Tanım 1. Bir $V$ vektör uzayı verilsin. Aşağıdaki özellikleri sağlayan bir $\langle\cdot, \cdot\rangle: V \times V \rightarrow \mathbb{R}$ fonksiyonuna $V$ üzerinde bir iç çarpım denir:
- Her $v, w \in V$ için $\langle v, w\rangle=\langle w, v\rangle$.
- Her $v, w, u \in V$ için
$$
\langle v, w+u\rangle=\langle v, w\rangle+\langle v, u\rangle .
$$
- Her $v, w \in V$ ve $r \in \mathbb{R}$ için
$$
\langle r v, w\rangle=r\langle v, w\rangle=\langle v, r w\rangle .
$$
- Sıfır olmayan her $v \in V$ için $\langle v, v\rangle>0$ ve $\left\langle 0_{V}, 0_{V}\right\rangle=0$.
Yukarıdaki temel örneğimize ek olarak bir de sonsuz boyutlu bir iç çarpım uzayı örneği verelim.
Örnek 1. $[0,1]$ aralığı üzerinde tanımlı gerçel değerler alan sürekli fonksiyonların kümesi aşikar toplama ve çarpmayla bir vektör uzayı olur. Bu uzay üstünde şu iç çarpımı tanımlayalım:
$$
\langle f, g\rangle:=\int_{0}^{1} f(x) g(x) \mathrm{d} x .
$$
İntegralin özelliklerini kullanarak bunun bir iç çarpım olduğunu kontrol etmek oldukça kolay.
Bir vektör uzayı üzerinde tanımlı bir iç çarpımın izomorfik uzaylara taşınabileceğine dikkat edelim. Yani $V$’nin üzerinde bir $\langle\cdot, \cdot\rangle$ iç çarpımı varsa ve $f: V \rightarrow W$ bir izomorfizmaysa
$$
\left\langle w_{1}, w_{2}\right\rangle:=\left\langle f^{-1}\left(w_{1}\right), f^{-1}\left(w_{2}\right)\right\rangle .
$$
şeklinde tanımlanan fonksiyon $W$ üzerinde bir iç çarpım verir.
Ama bunun tersine izomorfik uzaylar üzerinde birbirinden farklı iç çarpımlar olabilir; hatta aynı uzay üzerinde iki farklı iç çarpım olabilir. Mesela $\mathbb{R}^{n}$ üzerinde tanımlanan $v \cdot w$ iç çarpımı ve bir $\alpha$ pozitif gerçel sayısı için $\langle v, w\rangle:=\alpha(v \cdot w)$ şeklinde verilen iç çarpım $\alpha \neq 1$ olduğu sürece -görünüşte- farklı iç çarpımlar veriyor.
Bu bölümün geri kalanında, tersi söylenmediği sürece, $V$ üzerinde $\langle \cdot, \cdot \rangle$ olarak gösterilen bir iç çarpım olan bir vektör uzayı olacak.
Tanım 2. Alınan $v, w \in V$ için $\langle v, w\rangle=0$ oluyorsa $v$ ve $w$ birbirine diktir denir. (Bazı kaynaklarda ortogonal kelimesini de görebilirsiniz.) Bu durum
$$
v \perp w
$$
olarak gösterilir.
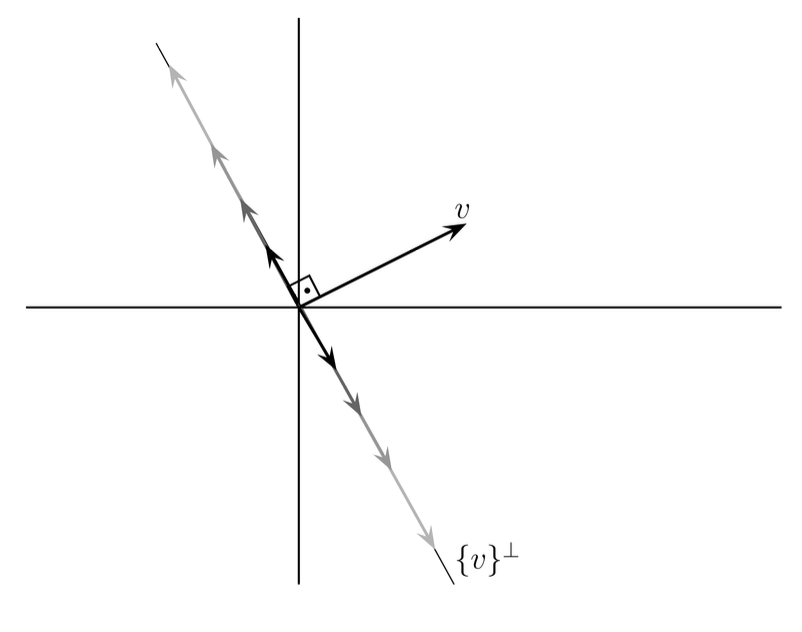
Örnek 2. Mesela $\mathbb{R}^{2}$’deki iç çarpımla $v=\left(\begin{array}{l}2 \\ 1\end{array}\right)$ vektörüne dik vektörlerin hangileri olduğuna bakalım. Bir
$$
\left(\begin{array}{l}
x \\
y
\end{array}\right)
$$
vektörü alalım. Bu vektörün $v$’ye dik olması için $2 x+y=0$ olmalı. Yani $y=-2 x$ olmalı. Bunu gerçel düzlemde çizdiğimizde $v$’ye dik vektörlerin gerçekten de bunlar olduğunu görürüz.
Daha genel olarak, verilen bir
$$
v=\left(\begin{array}{c}
a \\
b
\end{array}\right)
$$
vektörüne dik olan vektörleri anlayalım. Mesela
$$
\left(\begin{array}{l}
x \\
y
\end{array}\right)
$$
vektörü yukarıda verilen vektöre dik olsun. O zaman
$$
a x+b y=0
$$
olmalı. Eğer $b$ sıfır değilse $y=-\frac{a}{b} x$ olur. Yani o durumda $v$’ye dik olan bir vektör
$$
\left(\begin{array}{r}
x \\
-\frac{a}{b} x
\end{array}\right)
$$
şeklinde olmalı.
Benzer biçimde eğer $a$ sıfır değilse $v$’ye dik vektörler
$$
\left(\begin{array}{r}
-\frac{b}{a} y \\
y
\end{array}\right)
$$
şeklinde olur. (Bunları da görsel olarak anlamaya çalışın.)
Eğer hem $a$ hem de $b$ sıfırsa $v$ vektörü sıfır vektörüdür ve $\mathbb{R}^{2}$’nin her elemanının bu vektöre dik olduğu oldukça açık.
Tanım 3. Verilen bir $S \subseteq V$ altkümesinin her elemanına dik vektörlerin kümesini $S^{\perp}$ olarak göstereceğiz. Yani
$$
S^{\perp}:=\{v \in V: \text { her } s \in S \text { için } v \perp s\} .
$$
Önsav 1. $V$’nin $S$ ve $T$ altkümeleri için aşağıdakiler doğrudur.
- Eğer $S \subseteq T$ ise $T^{\perp} \subseteq S^{\perp}$ olur.
- $S^{\perp}$ bir altuzayıdır.
- $S^{\perp}=\langle S\rangle^{\perp}$.
Kanıt. İlk kısmı kanıtlamak için $S \subseteq T$ olduğunu varsayalım ve $v \in T^{\perp}$ alalım. Yani her $t \in T$ için $v \perp t$ olacak. Bu durumda $S \subseteq T$ olduğu için her $s \in S$ için $v \perp s$ olacağından $v \in S^{\perp}$ elde ederiz.
İkincisini kanıtlamak için $v, w \in S^{\perp}$ ve $r \in \mathbb{R}$ alalım. Yani her $s \in S$ için $\langle s, v\rangle=\langle s, w\rangle=0$. Demek ki $\langle s, w+v\rangle=\langle s, v\rangle+\langle s, w\rangle=0$. Benzer biçimde $\langle s, r v\rangle=r\langle s, v\rangle=0$. Yani $S^{\perp}$ toplam ve skaler çarpma altında kapalı; yani $V$’nin bir altuzayı.
Son kısım için ilk olarak -ilk kısmı kullanarak- $\langle S\rangle^{\perp} \subseteq S^{\perp}$ olduğuna dikkat edelim. Diğer içindeliği göstermek için $v \in S^{\perp}$ ve $w \in\langle S\rangle$ alıp $\langle v, w\rangle=0$ olduğunu gösterilim. Bunun için $w=r_{1} s_{1}+\cdots+r_{n} s_{n}$ olacak şekilde $s_{1}, \ldots, s_{n} \in S$ alalım. Şimdi her $i$ için $\left\langle v, s_{i}\right\rangle=0$ olduğunu biliyoruz. Yine iç çarpımın özelliklerini kullanarak
$$
\langle v, w\rangle=r_{1}\left\langle v, s_{1}\right\rangle+\cdots+r_{n}\left\langle v, s_{n}\right\rangle=0
$$
olduğu gösterilir. $\quad \square$
Bu önsavın son kısmından çıkardığımız sonuç $S^{\perp}$’i incelemek için $S$’nin bir altuzay olduğunu varsayabileceğimiz.
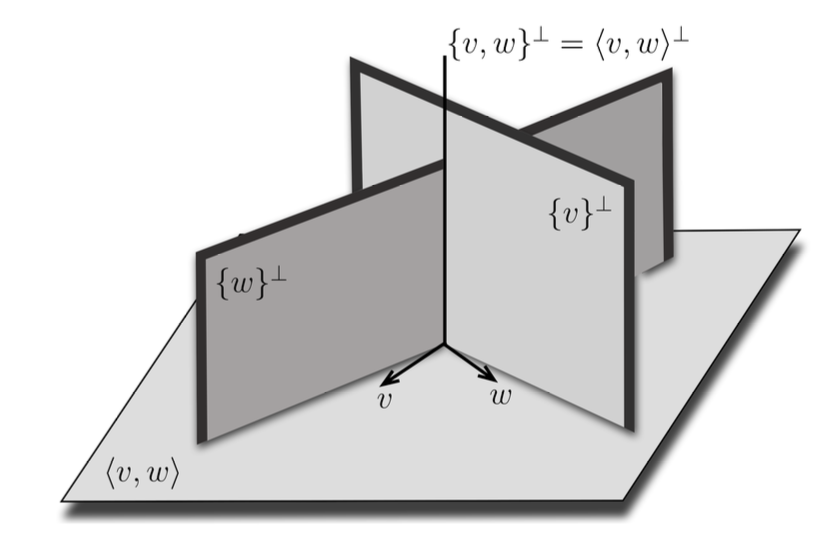
Yine bir örnekte buna bakalım. Yukarıda tek bir vektöre dik elemanları sınıflandırmıştık; bu da bir doğrunun bütün elemanlarına dik olan elemanları sınıflandırmak demek. Şimdi de bir adım daha öteye gidip bir düzleme dik vektörleri anlamaya çalışalım.
Örnek 3. Şu düzleme bakalım:
$$
W= \left\{ \left(\begin{array}{l}
x \\
y \\
z
\end{array}\right): x+y+z=0 \right\} .
$$
Bu düzlemin bir tabanı
$$
\left\{ \left(\begin{array}{r}
1 \\
0 \\
-1
\end{array}\right),\,\left(\begin{array}{r}
1 \\
-1 \\
0
\end{array}\right) \right\}
$$
olur. Yani $W^{\perp}$ uzayını anlamak için bu vektörlere dik olan vektörleri bulmak yeterli. Bir
$$
\left(\begin{array}{l}
a \\
b \\
c
\end{array}\right) \in \mathbb{R}^{3}
$$
alalım. Bu vektörün $W$’ya dik olması
$$
a-c=0 \quad \text { ve } \quad b-c=0
$$
olması demek. O halde $W^{\perp}$’teki vektörler
$$
\left(\begin{array}{l}
a \\
a \\
a
\end{array}\right)
$$
formunda. Yine bunu görsel olarak kontrol edebilirsiniz.
Eğer çalıştığımız iç çarpım uzayı $\mathbb{R}^{n}$ ise, bir $S$ altkümesine dik elemanları matrisleri kullanarak ifade edebiliriz: Satırları $S$’nin elemanlarını devrikleri olan $A$ matrisiyle belirlenen homojen sistemin çözüm kümesi $S^{\perp}$ olur. Yani eğer
$$
S=\{a_{1}, \ldots, a_{m}\}
$$
ise
$$
A=\left(\begin{array}{c}
a_{1}^{t} \\
a_{2}^{t} \\
\vdots \\
a_{m}^{t}
\end{array}\right)
$$
olur. Şimdi $A$ ile belirlenen homojen lineer sisteminin çözüm uzayının tam olarak $S^{\perp}$ olduğuna dikkat edelim. Bunun tersine, her matrisin verdiği homojen sistemin çözüm uzayını da o matrisin satırlarına dik vektörler olarak ifade edebiliriz.
Mesela yukarıdaki örnekte
$$
A=\left(\begin{array}{rrr}
1 & 0 & -1 \\
1 & -1 & 0
\end{array}\right)
$$
oluyor.
Uzunluk ve Uzaklık
Elimizde bir iç çarpım olduğu zaman, “bir vektörün uzunluğu”, “iki vektörün birbirlerine uzaklığı” gibi kavramları tanımlayabiliriz. Bu kavramlar, $\mathbb{R}^{n}$’nin iç çarpmasıyla bildiğimiz Öklid uzaklığ kavramlarına karşılık gelecek.
Tanım 4. Verilen bir $v \in V$ vektörünün uzunluğu
$$
\|v\|:=\sqrt{\langle v, v\rangle} .
$$
olarak tanımlanır. (Bazen $v$’nin normu da denilir.)
Bir vektörü $r$ skaleriyle çarpmak uzunluğunu $|r|$ ile çarpma etkisi yapar:
$$
\begin{aligned}
\|r v\| & =\sqrt{\langle r v, r v\rangle} \\
& =\sqrt{r^{2}\langle v, v\rangle} \\
& =|r| \sqrt{\langle v, v\rangle} \\
& =|r|\|v\| .
\end{aligned}
$$
Peki bunun benzerini toplama için yapabilir miyiz? Yani iki vektörün toplamının uzunluğu, uzunluklarının toplamı mıdır? Bir sonraki örnekte görülebileceği gibi bu mümkün değil.
Örnek 4. $\mathbb{R}^{2}$ üzerindeki iç çarpımla $v=\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)$ vektörünün uzunluğu $\sqrt{v_{1}^{2}+v_{2}^{2}}$ olur. Bir de $w=\left(\begin{array}{c}w_{1} \\ w_{2}\end{array}\right)$ vektörü alıp $v+w$’nun uzunluğuna bakalım:
$$
\|v+w\|=\sqrt{\left(v_{1}+w_{1}\right)^{2}+\left(v_{2}+w_{2}\right)^{2}} .
$$
Örneğin $v=\left(\begin{array}{l}1 \\ 0\end{array}\right)$, $w=\left(\begin{array}{l}0 \\ 1\end{array}\right)$ vektörlerinin her birinin uzunluğu $1$ ve toplamlarının uzunluğu $\sqrt{2}$. Yani genel olarak
$$
\|v+w\| \neq \|v\| + \|w\| .
$$
Ama vektörler birbirlerine dik olduğunda, hepimizin çok iyi bildiği Pisagor eşitliği var.
Önerme 1. Birbirine dik $v$,$w$ vektörleri için şu doğrudur:
$$
\|v+w\|^{2} = \|v\|^{2} + \|w\|^{2} .
$$
Kanıt. Sadece tanımları yazınca kanıt bitiyor:
$$
\begin{aligned}
\|v+w\|^{2} & =\langle v+w, v+w\rangle \\
& =\langle v, v\rangle+\langle v, w\rangle+\langle w, v\rangle+\langle w, w\rangle \\
& =\|v\|^{2}+\|w\|^{2}
\end{aligned}
$$
(Diklikten dolayı, $\langle v, w\rangle=\langle w, v\rangle=0$.) $\quad \square$
Yine sadece tanımları yerine koyarak şu da kanıtlanabilir. (Bunu okura alıştırma olarak bırakıp, yerine D. S. Wise’ın sözsüz bir ispatını veriyoruz. Bir paralelkenarda köşegen uzunluklarınn kenar vektörlerinin toplaminın ve farkının uzunlukları olduğunu hatırlatalım.)
Önerme 2. (Paralelkenar Kuralı) Her $v, w \in V$ için
$$
\|v+w\|^{2}+\|v-w\|^{2}=2 \left(\|v\|^{2}+\|w\|^{2} \right)
$$
eşitliği sağlanır.
Kanıt. Vektörler doğrusalsa önerme toplamın karesi ve farkın karesi özdeşliklerinin bir sonucudur. Vektörler doğrusal değilse bir paralelkenar oluştururlar:
Paralelkenar Kuralında vektörlerin dik olduğunu kabul ettiğimizde Pisagor Teoremi’nin ortaya çıktığını görüyoruz. Pisagor Teoremi’nin hipotezindeki diklik varsayımını bıraktığımızda da, eşitlik yerine üçgen eşitsizliğini elde edeceğiz ama bunu yapmak için şu önemli sonuca da ihtiyacımız var.
Önerme 3. (Cauchy-Schwarz Eşitsizliği) Her $v, w \in V$ için
$$
|\langle v, w\rangle| \leq \|v\| \| w\|
$$
olur.
Kanıt. Eğer $v$ veya $w$ sıfırsa, eşitsizlik bariz biçimde doğru. O yüzden ikisinin de sıfır olmadığını varsayalım ve $a=\frac{\langle v, w\rangle}{\langle w, w\rangle}$ olsun. Bu durumda $v-a w$ ile $a w$’nun birbirlerine dik olduğuna dikkat edelim. Yani Pisagor eşitliğinden
$$ \|v\|^{2}=\|v-a w\|^{2}+\|a w\|^{2}
$$
oluyor. Yani
$$
\begin{aligned}
\|v\|^{2} & \geq \left\| \frac{\langle v, w\rangle}{\langle w, w\rangle} w \right\| ^{2} \\
& =\frac{\langle v, w\rangle^{2}}{\langle w, w\rangle^{2}}\|w\|^{2} \\
& =\frac{\langle v, w\rangle^{2}}{\|w\|^{4}}\|w\|^{2}
\end{aligned}
$$
Bu durumda da
$$
(\|v\| \|w\|)^{2} \geq\langle v, w\rangle^{2}
$$
elde ederiz. Dolayısıyla karekökleri alarak istediğimiz sonucu kanıtlamış oluruz. $\quad \square$
Şimdi üçgen eşitsizliğini ifade edip kanıtlayabiliriz.
Önerme 4. Her $v, w \in V$ için
$$
\|v+w\| \leq \|v\|+\|w\|
$$
olur.
Kanıt. İlk olarak $v+$’nun uzunluğunun karesine bakalım:
$$
\begin{aligned}
\|v+w\|^{2} & =\langle v+w, v+w\rangle \\
& =\langle v, v\rangle+\langle v, w\rangle+\langle w, v\rangle+\langle w, w\rangle \\
& =\|v\|^{2}+\|w\|^{2}+2\langle v, w\rangle \\
& \leq \|v\|^{2}+\|w\|^{2}+2\|v\| \|w\| \\
& =(\|v\|+\|w\|)^{2}
\end{aligned}
$$
elde ederiz ve iki tarafın da karekökleri alarak üçgen eşitsizliğini kanıtlamış oluruz.$\quad \square$
Buna niçin üçgen eşitsizliği dediğimiz aşağıdaki tanımla daha anlaşılır olacak.
Tanım 5. Verilen $v, w \in V$ vektörlerinin birbirlerine uzaklığı
$$
\|v-w\|
$$
olarak tanımlanır ve $d(v, w)$ olarak gösterilir.
Şimdi Önerme 4, uzaklık kavramıyla şu hale dönüşüyor.
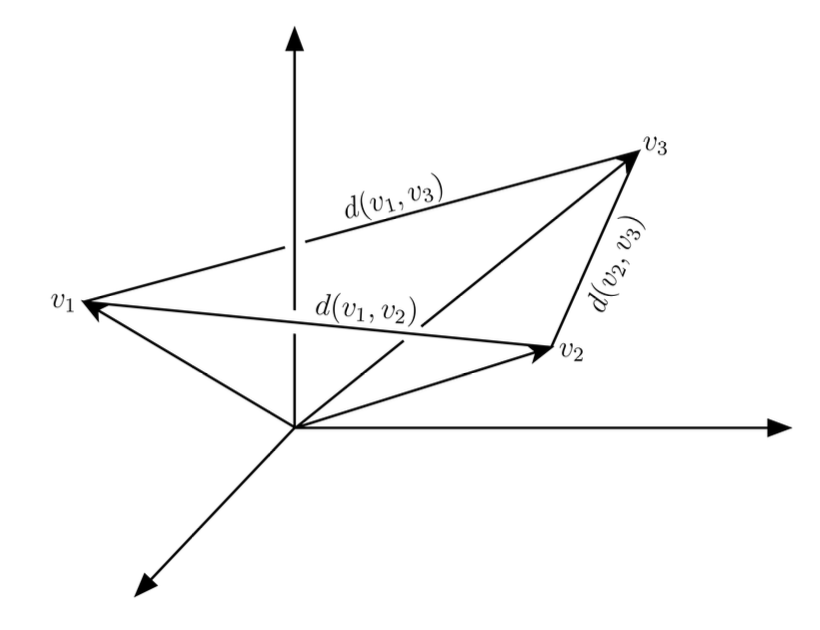
Sonuç 1. Her $v_{1}, v_{2}, v_{3} \in V$ için
$$
d\left(v_{1}, v_{3}\right) \leq d\left(v_{1}, v_{2}\right)+d\left(v_{2}, v_{3}\right)
$$
olur.
Kanıt.
$$
\begin{aligned}
d\left(v_{1}, v_{3}\right) & =\left\|v_{1}-v_{3}\right\| \\
& =\left\|v_{1}-v_{2}+v_{2}-v_{3}\right\| \\
& \leq\left\|v_{1}-v_{2}\right\|+\left\|v_{2}-v_{3}\right\| \\
& =d\left(v_{1}, v_{2}\right)+d\left(v_{2}, v_{3}\right) . \qquad \square
\end{aligned}
$$
Doğrulara İzdüşüm
Standart taban elemanlarından birini, mesela ilkini, aldığımızda verilen herhangi bir vektörün o taban elemanının belirlediği koordinata izdüşümünden bahsedebiliriz. Mesela $\mathbb{R}^{2}$’de $e_{1}$’in belirlediği altuzay $x$-ekseni olur ve verilen bir vektörün bu altuzaya izdüşümü o vektörün $x$-koordinatı olur. Aslında bunu yaparken başladığımız vektörün standart taban elemanı olmasının özel bir anlamı yok. Sıfır olmayan herhangi bir vektörle başlasaydık da aynısını yapabilirdik.
Önerme 5. Sıfır olmayan bir $v \in V$ verilsin. O zaman her $w \in V$ için $w-r v$, $v$’ye dik olacak biçimde bir $r \in \mathbb{R}$ vardır.
Kanıt. Bizim işimize yarayacak olan $r$ şudur:
$$
r=\frac{\langle v, w\rangle}{\langle v, v\rangle} .
$$
(Burada $v$ sıfır vektörü olmadığı için $\langle v, v\rangle$ sayısının sıfır olmadığına dikkat edelim.) Şimdi $v$ ile $w-r v$ vektörlerinin birbirlerine dik olduklarını gösterelim:
$$
\begin{aligned}
\langle v, w-r v\rangle & =\langle v, w\rangle+(-r)\langle v, v\rangle \\
& =\langle v, w\rangle-\frac{\langle v, w\rangle}{\langle v, v\rangle}\langle v, v\rangle\\ &=0. \qquad \square
\end{aligned}
$$
Tanım 6. Yukarıdaki önermedeki $r$’ye $w$’nun $v$ yönündeki bileşeni ve $rv$’ye de $w$’nun $v$’ye izdüşümü denir.
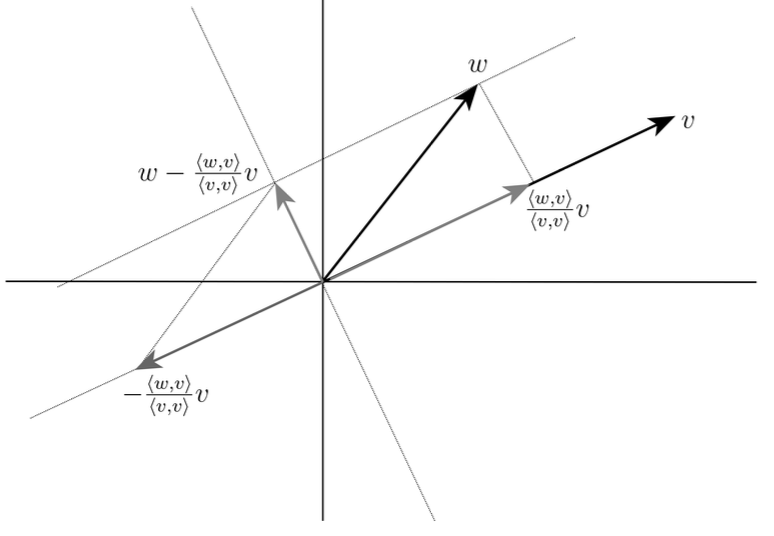
Eğer $v$’nin uzunluğu $1$ ise $r$’nin $\langle v, w\rangle$ olduğuna dikkat edelim.
Örnek 5. Herhangi bir
$$
w=\left(\begin{array}{c}
w_{1} \\
w_{2} \\
\vdots \\
w_{n}
\end{array}\right)
$$
vektörünün $\mathbb{R}^{n}$’nin standart taban elemanlarından $e_{i}$ yönündeki bileşenini
$$
\frac{e_{1} \cdot w}{e_{i} \cdot e_{i}}=\frac{w_{i}}{1}=w_{i}
$$
olur. O yöndeki izdüşümü de
$$
w_{i}\left(\begin{array}{c}
0 \\
0 \\
\vdots \\
1 \\
\vdots \\
0
\end{array}\right)=\left(\begin{array}{c}
0 \\
0 \\
\vdots \\
w_{i} \\
\vdots \\
0
\end{array}\right)
$$
olur. Bu son vektörün $w$’nun $i$’inci koordinata bildiğimiz anlamdaki izdüşümü olduğuna dikkat edelim.
Önerme 6. Bir $w$’nun $v$’ye izdüşümü, $v$’nin gerdiği doğrunun üstündeki $w$’ya en yakın vektördür. Yani $r=\frac{\langle v, w\rangle}{\langle v, v\rangle}$ olmak üzere her $s \in \mathbb{R}$ için
$$
d(w, r v) \leq d(w, s v)
$$
olur.
Kanıt. Herhangi bir $s \in \mathbb{R}$ alalım. İzdüşümün tanımından dolayı $w-r v$ ile $v$ vektörleri birbirlerine dik olduğundan $w-r v$, $v$’nin gerdiği doğrudaki bütün vektöre de dik olur. Pisagor eşitliğini kullanarak
$$
\|w-r v\|^{2}+\|(r-s) v\|^{2}=\|w-s v\|^{2}
$$
elde ederiz ve $\|(r-s) v\|^{2} \geq 0$ olduğundan
$$
\|w-r v\|^{2} \leq \|w-s v\|^{2}
$$
olur. Her iki tarafın karekökünü alarak
$$
d(w, r v) \leq d(w, s v)
$$
eşitsizliğini göstermiş oluruz. $\quad \square$
Gram-Schmidt Dikleştirme İşlemi
Tanım 7. Bir $ B= \{v_{1}, \ldots, v_{n} \}$ tabanı verilsin. Eğer her $i \neq j$ için $\langle v_{i}, v_{j}\rangle=0$ ise $B ‘ye bir dik taban denir. Buna ek olarak her $v_{i}$’nin uzunluğu $1$’se, $B$’ye birimdik taban denir.
Örnek 6. Bunun en temel örneği $\mathbb{R}^{n}$ üzerindeki standart taban: $ \{e_{1}, \ldots, e_{n} \}$. Farklı $i, j$ için $\left\langle e_{i}, e_{j}\right\rangle=0$ olduğu da her $e_{i}$’nin uzunluğunun $1$ olduğu da aşikar.
Örnek 7. Bir öncekinden daha ilginç olarak $\mathbb{R}^{2}$’nin şu tabanını alalım:
$$
B=\Bigg\{ \left(\begin{array}{l}
1 \\
1
\end{array}\right),\,\left(\begin{array}{r}
1 \\
-1
\end{array}\right) \Bigg\} .
$$
Bir kez daha bu tabanın dik olduğunu göstermek kolay; ama bu tabandaki vektörlerin uzunlukları $\sqrt{2}$. Bu tabanı birimdik bir tabana dönüştürmek için her iki vektörü de $\frac{1}{\sqrt{2}}$ ile çarpalım. Yani
$$
B^{\prime}= \Bigg\{\left(\begin{array}{c}
1 / \sqrt{2} \\
1 / \sqrt{2}
\end{array}\right),\,\left(\begin{array}{r}
1 / \sqrt{2} \\
-1 / \sqrt{2}
\end{array}\right) \Bigg\}
$$
hala dik bir taban ve her elemanının uzunluğu $1$. Aslında burada yaptığımızı her zaman yapabildiğimizi biraz ileride göreceğiz.
Verilen bir $v=\left(\begin{array}{l}x \\ y\end{array}\right)$ vektörünün $B^{\prime}$ tabanına göre koordinatlarını yazalım:
$$
a\left(\begin{array}{l}
1 / \sqrt{2} \\
1 / \sqrt{2}
\end{array}\right)+b\left(\begin{array}{r}
1 / \sqrt{2} \\
-1 / \sqrt{2}
\end{array}\right)=\left(\begin{array}{l}
x \\
y
\end{array}\right)
$$
olacak şekilde $a, b \in \mathbb{R}$ bulmak istiyoruz. (Bu $a$ ve $b$, $x$ ve $y$ cinsinden yazllacak.) Yani
$$
\left(\begin{array}{c}
\frac{1}{\sqrt{2}}(a+b) \\
\frac{1}{\sqrt{2}}(a-b)
\end{array}\right)=\left(\begin{array}{l}
x \\
y
\end{array}\right)
$$
olmalı. Yani
$$
a=\frac{1}{\sqrt{2}}(x+y) \quad \text { ve } \quad b=\frac{1}{\sqrt{2}}(x-y) .
$$
Benzer biçimde bir de $w=\left(\begin{array}{c}s \ t\end{array}\right)$ vektörü alalım. Şimdi
$$
\langle v, w\rangle=x s+y t
$$
oluyor. Bir de $v$ ve $w$’nun koordinatlarının bildiğimiz iç çarpımına bakalım:
$$
\left(\begin{array}{l}
1 / \sqrt{2}(x+y) \\
1 / \sqrt{2}(x-y)
\end{array}\right) \cdot\left(\begin{array}{l}
1 / \sqrt{2}(s+t) \\
1 / \sqrt{2}(s-t)
\end{array}\right)=x s+y t .
$$
Yani $v$ ile $w$’nun iç çarpımını almak yerine bu vektörlerin $B^{\prime}$ tabanına göre koordinatlarının iç çarpımını alabilirdik. Bu genel olarak doğru. Bunu kaydedelim.
Önerme 7. Bir $V$ iç çarpım uzayının bir $B=\{ v_{1}, \ldots, v_{n} \}$ birimdik tabanı verilsin. Alınan $v, w \in V$ vektörlerinin $B$’ye göre koordinatlar $a, b$ olsun. O zaman
$$
\langle v, w\rangle=a^{t} \cdot b^{t}
$$
olur.
Kanıt. Elimizdeki vektörleri şu şekilde yazalım:
$$
v=a_{1} v_{1}+\cdots+a_{n} v_{n} \quad \text{ ve } \quad w=b_{1} v_{1}+\cdots+b_{n} v_{n} .
$$
Bu durumda
$$
\begin{aligned}
\langle v, w\rangle & =\left\langle a_{1} v_{1}+\cdots+a_{n} v_{n}, b_{1} v_{1}+\cdots+b_{n} v_{n}\right\rangle \\
& =\sum_{i, j} a_{i} b_{j}\left\langle v_{i}, v_{j}\right\rangle \\
& =a_{1} b_{1}+\cdots+a_{n} b_{n} \\
& =a^{t} \cdot b^{t} \qquad \square
\end{aligned}
$$
Bir önceki örnekte yaptığımız gibi üzerinde iç çarpım olan her sonlu boyutlu vektör uzayının her tabanını dik bir tabana dönüştürebiliriz.
Teorem 1. (Gram-Schmidt İşlemi) Sonlu boyutlu bir $V$ iç çarpım uzayı ve her $i \neq j$ için $w_{i} \perp w_{j}$ olacak şekilde lineer bağımsız $\{w_{1}, \ldots, w_{m}\}$ kümesi verilsin. O zaman $\{w_{1}, \ldots, w_{m}, v_{m+1}, \ldots, v_{n} \}$, $V$’nin dik bir tabanı olacak şekilde $v_{m+1}, \ldots, v_{n}$ vektörleri vardır.
Kanıt. İlk olarak ${w_{1}, \ldots, w_{m}}$’yi $V$’nin bir tabanına genişletelim:
$$
\{w_{1}, \ldots, w_{m}, v_{m+1}^{\prime}, \ldots, v_{n}^{\prime} \} .
$$
Tabii ki bu tabanın dik olması için bir sebep yok. Sırasıyla $v_{i}^{\prime}$ vektörlerini değiştirerek dik bir taban elde edeceğiz: $W_{1}=\left\langle w_{1}, \ldots, w_{m}, v_{m+1}^{\prime}\right\rangle$ olsun ve $v_{m+1}$ olarak şu vektörü alalım:
$$
v_{m+1}^{\prime}-\frac{\left\langle v_{m+1}^{\prime}, w_{1}\right\rangle}{\left\langle w_{1}, w_{1}\right\rangle} w_{1}-\cdots-\frac{\left\langle v_{m+1}^{\prime}, w_{m}\right\rangle}{\left\langle w_{m}, w_{m}\right\rangle} w_{m} .
$$
(Burada yaptığımız, $v_{m+1}^{\prime}$ vektörünün $w_{1}, \ldots, w_{m}$ vektörlerinin gerdiği altuzaya izdüşümünü bulup $v_{m+1}^{\prime}$ ‘den bunu çıkartarak o vektörlere dik bir vektör bulmak.)
Şimdi $\{w_{1}, \ldots, w_{m}, v_{m+1}\}$ kümesinin $W_{1}$’in bir tabanı olduğu açık. Yani sadece her $i$ için $v_{m+1} \perp w_{i}$ olduğunu göstermek gerekli. Bunun için $\langle v_{m+1}, w_{i}\rangle$ sayısını
$$
\langle v_{m+1}^{\prime}-\frac{\left\langle v_{m+1}^{\prime}, w_{1}\right\rangle}{\left\langle w_{1}, w_{1}\right\rangle} w_{1}-\cdots-\frac{\left\langle v_{m+1}^{\prime}, w_{m}\right\rangle}{\left\langle w_{m}, w_{m}\right\rangle} w_{m}, w_{i}\rangle
$$
olarak yazalım. Bu son sayının
$$
\left\langle v_{m+1}^{\prime}, w_{i}\right\rangle- \langle w_{i}, \frac{\left\langle v_{m+1}^{\prime}, w_{i}\right\rangle}{\left\langle w_{i}, w_{i}\right\rangle} w_{i}\rangle=0
$$
olduğu açık. Yani $v_{m+1} \perp w_{i}$.
Bundan sonraki adımlar da benzer biçimde (tümevarımla) yapılıp, $v_{m+2}, \ldots, v_{n}$ vektörleri elde edilir. $\quad \square$
Sonuç 2. Sıfır uzayından farklı sonlu boyutlu her uzayın dik bir tabanı vardır. Hatta bu bulduğumuz dik tabanı birimdik bir tabana da dönüşürebiliriz.
Örnek 8. $V$, $\mathbb{R}^{4}$’ün şu vektörlerle gerilen altuzayı olsun:
$$
v_{1}=\left(\begin{array}{r}
-1 \\
2 \\
1 \\
0
\end{array}\right),\quad v_{2}=\left(\begin{array}{r}
-2 \\
0 \\
1 \\
1
\end{array}\right),\quad v_{3}=\left(\begin{array}{r}
2 \\
-3 \\
0 \\
0
\end{array}\right) .
$$
Bu uzayın ilk olarak, dik bir tabanını bulalım; bunun için ilk vektör olarak $v_{1}$’in kendisini alalım. Şimdi $v_{2}$’yi değiştirmemiz lazım:
$$
\begin{aligned}
v_{2}^{\prime} & =v_{2}-\frac{\left\langle v_{1}, v_{2}\right\rangle}{\left\langle v_{1}, v_{1}\right\rangle} v_{1} \\
& =\left(\begin{array}{r}
-2 \\
0 \\
1 \\
1
\end{array}\right)-1 / 2\left(\begin{array}{r}
-1 \\
2 \\
1 \\
0
\end{array}\right) \\
& =\left(\begin{array}{r}
-3 / 2 \\
-1 \\
1 / 2 \\
1
\end{array}\right) .
\end{aligned}
$$
Sırada $v_{1}$ ve $v_{2}^{\prime}$’yi kullanarak $v_{3}^{\prime}$ vektörünü bulmak var:
$$v_{3}^{\prime}=v_{3}-\frac{\left\langle v_{1}, v_{3}\right\rangle}{\left\langle v_{1}, v_{1}\right\rangle} v_{1}-\frac{\left\langle v_{2}^{\prime}, v_{3}\right\rangle}{\left\langle v_{2}^{\prime}, v_{2}^{\prime}\right\rangle} v_{2}^{\prime}=\left(\begin{array}{r}10 / 3 \\ -17 / 3 \\ -4 / 3 \\ 0\end{array}\right)$$
O halde
$$
\left\{\left(\begin{array}{r}
-1 \\
2 \\
1 \\
0
\end{array}\right),\,\left(\begin{array}{r}
-3 / 2 \\
-1 \\
1 / 2 \\
1
\end{array}\right),\,\left(\begin{array}{r}
10 / 3 \\
-17 / 3 \\
-4 / 3 \\
0
\end{array}\right) \right\}
$$
$V$’nin dik bir tabanı olur. Şimdi bu tabanın elemanlarını sırasıyla $\frac{1}{\sqrt{6}}$, $\frac{3}{\sqrt{2}}$ ve $\frac{1}{3 \sqrt{5}}$ skalerleriyle çarparsak birimdik bir taban elde ederiz.
Önerme 8. Bir $V $ vektör uzayının $\{v_{1}, \ldots, v_{m}, w_{1}, \ldots, w_{n}\}$ dik tabanını alalım. $V_{1}= \langle v_{1}, \ldots, v_{m} \rangle $ ve $V_{2}= \langle w_{1}, \ldots, w_{n}\rangle $ olsun. O zaman $V_{1}^{\perp}=V_{2}$.
Kanıt. İlk olarak bir $v \in V_{1}^{\perp}$ alalım ve
$$
v=a_{1} v_{1}+\cdots+a_{m} v_{m}+b_{1} w_{1}+\cdots+b_{n} w_{n}
$$
olarak yazalım. Her $i=1, \ldots, m$ için $\langle v, v_{1}\rangle$ iç çarpımı hem $0$’a hem de $a_{i}\|v_{i}\|^{2}$’ye eşit. Demek ki $a_{i}=0$ olmalı. Yani
$$
v=b_{1} w_{1}+\cdots+b_{n} w_{n} \in V_{2} .
$$
Şimdi de $v \in V_{2}$ olsun. Yani
$$
v=b_{1} w_{1}+\cdots+b_{n} w_{n} \in V_{2} .
$$
olacak şekilde $b_{1}, \ldots, b_{n} \in \mathbb{R}$ var. Bu durumda da her $i=1, \ldots, m$ için $\langle v, v_{i}\rangle=0$ olduğu aldığımız tabanın dik olmasından dolayı açık. $\quad \square$
Sonuç 3. Her $W \subseteq V$ için
$$
\operatorname{dim} W+ \operatorname{dim} W^{\perp}= \operatorname{dim} V .
$$

