Yazar: Ümit Işlak (umitislak@gmail.com)
Sayı: 111, 2022-1
Bir yatırımcıda şu anki değeri 25 lira olan bir hisse senedi olduğunu varsayalım. Yatırımcımız hisseyi hissenin değeri ya 10 liraya düşerse ya da 40 liraya ulaşırsa elinden çıkarmaya karar vermiş. Diyelim ki hisse senedi her seferinde ya $p$ olasılıkla bir lira yukarı çıkabiliyor ya da $q = 1-p$ olasılıkla bir lira aşağı inebiliyor. Bu durumda yatırımcının 40 liraya ulaşıp bu yatırımdan kârlı çıkması olasılığı nedir? Finans piyasalarını oldukça basit ve pek gerçekçi görünmeyen bir şekilde modelleyen bu sorumuz pek çok sahadaki birçok problemde doğrudan ya da alttan alta ortaya çıkan ve olasılık teorisinde bir klasik olan “Kumarbazın Sonu” problemidir.
Olasılık teorisinin başlangıcı sıklıkla 1650’li yıllarda gerçekleşen Blaise Pascal ile Pierre Fermat arasındaki mektuplaşmalarla ilişkilendirilir. Bu yazışmalarda kumardan gelen motivasyonla çeşitli yazı-tura ve zar oyunları irdelenmiş ve ileride önemli yerlere (örneğin tıpkı yukarıdaki örneğimizdeki gibi finans matematiğine) oturtulacak neticelerin temelleri atılmıştır. Kumarbazın Sonu problemi de Pascal ile Fermat arasında tartışılan sorulardan biridir. Dileyenler [1] numaralı referanstan ikilinin arasında geçmiş yazışmalar hakkında daha detaylı bilgi edinebilirler.

Tarihsel olarak sorumuz ilk defa Fermat ile Pascal arasında geçen tartışmalarda formülleştirilmiş olsa da problemin günümüzdeki ve aşağıdaki tartışacağımız hali Christiaan Huygens’in 1656-1657 yıllarında yaptığı çalışmalarla ortaya çıkmıştır. Huygens 1629 ile 1695 arasında yaşamış Hollandalı bir bilim insanı ve fantastik buluşların sahibidir.
Kendisinin çalışma sahalarını ve eserlerini sıralamak dahi çok güç. Sarkaçlı saat, Huygens motoru, Satürn halkalarının açıklanması, Huygens merceği gibi birkaç anahtar kelime dahi etki sahasını özetlemeye yeterli. Olasılık teorisine dair ilk kitabın da 1673 yılında kendisi tarafından yazıldığını not düşmemiz gerekli: De Ratiociniis in Ludo Aleae – Şans Oyunlarındaki Olasılıklar.
Burada işin tarih kısmına daha fazla girmiyoruz, dileyenler oldukça fazla detay içeren [2] ve [3] referanslarına bakabilirler. Biz şimdi sorumuzun Huygens tarafından formülleştirilmiş, günümüzdeki versiyonunu ifade ettikten sonra takip eden bölümde de bu soruya bir çözüm sunacağız.
Kumarbazın sonu problemi. $i \in \mathbb{N} = \{1,2,3,\ldots\}$ lirası olan bir kumarbaz düşünelim. Kumarbazımız her oyunda $p \in (0,1)$ olasılıkla bir lira kazansın, $q = 1 -p $ olasılıkla ise bir lira kaybetsin. Her bir oyunun birbirinden bağımsız olduğunu varsayarsak kumarbazın $N \geq i+1$ liraya $0$ liradan önce ulaşma olasılığı, nedir? Bir başka deyişle kumarhanedeki tüm paranın kazanılma olasılığı nedir?
Burada kumarbazın ilk başta $i$ lirası olduğunu varsaydığımıza ve kumarbaz $N$’ye ulaştığında oyun bittiğine göre kumarhanenin başlangıçta $N – i$ lirası olduğunu varsaymamız gerekiyor. Gerçek hayatta $N$ tabii ki oldukça büyük bir değer, peki hiç bir kumarbazın kumarhanenin tüm parasına konduğunu gördünüz mü? Genellikle tam tersi olur, o yüzden bu problemin ismini aslında “Kumarbazın Hazin Sonu” da koyabiliriz.
Problemin çözümüne geçmeden önce son olarak bir de örneğe bakalım. Aşağıdaki şekilde oyuncumuzun $i=2$ liradan başladığı ve $N = 5$ olan iki olası durumu görüyoruz
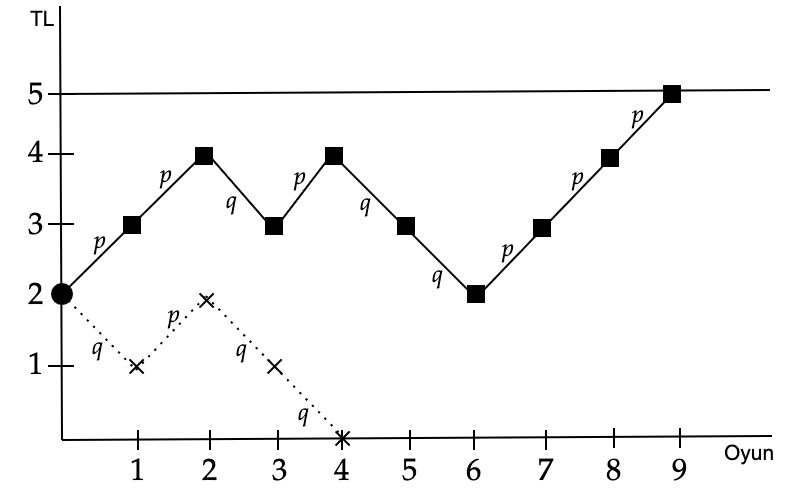
Düz çizgi olan durumda kumarbazın şansı yaver gitmiş ve dokuzuncu elin sonunda tüm parayı kazanmış. Bu yolu takip ederek bu durumun olasılığının $p^6 q^3$ olduğunu görüyoruz. Öte yandan kesik çizgili duruma bakarsak bu sefer dördüncü elin sonunda kumarbazın tüm parasını kaybettiğini görmekteyiz. Bu durumun olasılığını da kesikli çizgileri takip ederek $pq^3$ olarak bulabiliriz.
Kolayca görüleceği üzere 2 liradan başladığımız zaman 0 liradan önce 5 liraya ulaşabileceğimiz sonsuz farklı durum olabilir. Sorumuzda da tüm bu durumların olasılıklarının toplamı sorulmakta. Haydi çözüme geçelim.
Çözüm
$N \in \mathbb{N}$ değerini sabitleyelim ve $i$ sayısı $0 \leq i \leq N$ olacak şekilde bir tamsayı olsun. $P_i$ ile kumarbazın $i$ lirayla başladığı sürecin sonunda $N$ liraya ulaşma olasılığını gösterelim. $P_0 = 0 $ ve $P_N = 1$ olduğu açık olduğuna göre $i= 1,2,\ldots,N – 1$ durumuna odaklanabiliriz.
Kumarbazın $i$ lirası varken oynadığı ilk elde ya kazanacak ya da kaybedecek, o halde $P_i$ olasılıklarımız şu ilişkiyi sağlamakta: $$P_i = p P_{i+1} + q P_{i-1}, \quad i=1,2,\ldots,N- 1.$$ $p+q = 1$ olduğuna göre son eşitlik, $$p P_i + q P_i = p P_{i+1} + q P_{i-1}, \quad i=1,2,\ldots,N- 1$$ olarak da yazılabilir. Ufak tefek birkaç işlemin ardından bu da bize,
$$P_{i+1} – P_i = \frac{q}{p} (P_i – P_{i-1}), \quad i=1,2,\ldots,N – 1$$ (1)
yineleme ilişkisini verir.
Şimdi, $P_0 = 0$ olduğunu not düşüp, (1) yinelemesini $i = 1,2,\ldots,N – 1$ değerleri için kullanırsak aşağıdaki eşitliklerin doğru olduğunu görüyoruz:
$$\begin{eqnarray*} P_1 – P_0 &=& P_1 \\ P_2 – P_1 &=& \frac{q}{p} (P_1 – P_0 ) = \frac{q}{p} P_1, \\ P_3 – P_2 &=& \frac{q}{p} (P_2 – P_1 ) = \left( \frac{q}{p} \right)^2 P_1, \\ &\vdots& \\ P_i – P_{i-1} &=& \frac{q}{p} (P_{i-1} – P_{i-2} ) = \left( \frac{q}{p} \right)^{i-1} P_1, \\ &\vdots& \\ P_N – P_{N – 1} &=& \frac{q}{p} (P_{N-1} – P_{N-2} ) = \left( \frac{q}{p} \right)^{N-1} P_1. \end{eqnarray*}$$
Bu denklemlerin ilk $i$ tanesini toplarsak her $i= 1,$ $2,\ldots,N$ için doğru olan, $$P_i = P_1 \left(1 + \left(\frac{q}{p} \right) + \left(\frac{q}{p} \right)^2 + \cdots + \left(\frac{q}{p} \right)^{i-1} \right)$$ ifadesine ulaşmış oluruz. Burada sonlu geometrik seriler için, toplam formülünü (Eğer $-1 <r < 1$ ve $n \in \mathbb{N}$ ise $\sum_{i=0}^n r^i = \frac{1- r^{n+1}}{1- r}$) kullandığımızda da $i=1,2,\ldots,N$ için
$$\begin{equation}\label{eqn:gamblerPi} P_i =\begin{cases} \frac{1 – (q / p)^i}{1 – (q/p)} P_1, & p \neq \frac{1}{2} \text{ ise,} \\ i P_1, & p = \frac{1}{2} \text{ ise,} \end{cases}\end{equation}$$
(2)
buluruz. Yani $P_i$’yi $P_1$ cinsinden ifade edebildik. Artık son olarak $P_1$’in ne olduğunu bulmak kaldı. Bu amaçla, $P_N = 1$ olduğunu hatırlar ve (2) eşitliğinde $i = N$ alırsak, $P_1$’in değeri,
$$ P_1 = \begin{cases} \frac{1 – (q / p)}{1 – (q / p )^N}, & p \neq \frac{1}{2} \text{ ise,}\\ \frac{1}{N}, & p = \frac{1}{2} \text{ ise,} \end{cases} $$
olacaktır. Bulduğumuz $P_1$ değerini (2)’de yerine koyduğumuzda aradığımız cevaba sonunda ulaşıyoruz:
Kumarbaz $i$ liradan başlarsa $N$ liraya ulaşma olasılığı
$$P_i =\begin{cases} \frac{1 – (q / p)^i}{1 – (q/p)^N}, & p \neq \frac{1}{2} \text{ ise,}\\ \frac{i}{N}, & p = \frac{1}{2} \text{ ise,}\\ \end{cases}$$
olacaktır.
$N$ sonsuza giderken,
$$P_i \rightarrow \begin{cases} 1 – \left( \frac{q}{p} \right)^i, & p > \frac{1}{2} \text{ ise,} \\ 0, & p \leq \frac{1}{2} \text{ ise,}\\ \end{cases} $$
yakınsaması gerçekleşecektir.
Buradaki limit hesabından, eğer $p> 1/ 2$ ise kumarbazın servetini sınırsızca arttırma olasılığının pozitif olduğunu, $p \leq 1/2$ durumundaysa böylesi bir durumun mümkün olamayacağını görmekteyiz. Bir örnek olarak $p = 3/4$ alırsak $i$ lirayla başladığımızda $P_i$ olasılığı $1 – \left( \frac{1}{3} \right)^i$ değerine yaklaşıyor. $i=10$ lirayla başladığık büyük $N$ değerleri için kumarhanenin tüm parasını ele geçirme olasılığımız yaklaşık olarak $1 – (2/3)^{10}$. Hemen hemen kesin gibi!
Yine kumarbazın 10 lirayla başladığını varsayıp $N = 100$ alırsak farklı $p$ değerleri için kumarbazın kazanma olasılığı aşağıdaki şekilde gösterilmekte.
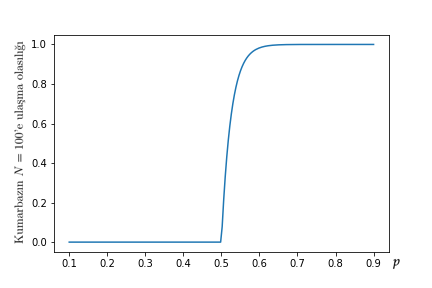
Kumarbazın yanılgısı
Tabii ki gerçek hayatta kumarhaneler $p < 1/2$ olacak şekilde oyunlar tasarlamaktalar ve olasılık teorisinde büyük sayılar kanunu olarak bilinen olgu sayesinde de uzun vadede oyunlardan galip çıkmaktalar: “Kasa kazanır.” Ancak kumarbazlar yine de oynamayı bırakamıyorlar, neden acaba? Oldukça karmaşık olan bu soruya cevap vermeye çalışmak dahi çok güç, ama sizlere kumarbazların oyun esnasında içine düştükleri bir yanılsamadan bahsedebilirim.
Bir yazı tura oyunu düşünelim. Bu oyunda üst üste çok fazla kez tura geldiyse insanlar artık bir sonraki seferde tura gelme olasılığının düştüğü fikrine kapılabilirler, ama bu tabii ki doğru değil. Kumarbazların bu tarz olasılık artması/azalmasına yönelik yanılsamalarının olasılık teorisi literatüründeki ismi Monte Carlo yanılgısı ya da Kumarbazın yanılgısıdır. İlk isimlendirme 18 Ağustos 1918 tarihinde Monte Carlo kumarhanesinde gerçekleşmiş bir olayla ilişkili. Bu talihli (ya da talihsiz) günde rulet oyununda üst üste tam olarak 26 kez siyah gelmiş ki bunun olasılığı da 1/66,6 milyon. İnsanların kaybettikleri paraları bir düşünün!
Burada altta yatan durum, olasılık teorisindeki terminolojiyle bağımsızlık’tır. Örnek olarak, adil bir parayla oynanan bir yazı-tura oyununda para atışlarının birbirinden bağımsız olması ve bundan ötürü o ana kadar kaç kez tura gelmiş olursa olsun bir sonraki seferde tura gelmesi olasılığının hâlâ $1/2$ olması verilebilir. Hayatın içinden ilgili bir diğer örnek olarak, yedi tane kız çocuğu olmuş bir kişinin sekizinci çocuğunun artık erkek olma olasılığının daha yüksek olduğu yanılsamasını gösterebiliriz. Örnekler çoğaltılabilir, sizlere bırakalım.
Kaynaklar
[1] http://www.socsci.uci.edu/~bskyrms/bio/readings/pascal_fermat.pdf Sayfa ziyaret tarihi: 12.01.2022.
[2] Edwards, A. W. F., Pascal’s problem: The gambler’s ruin. International Statistical Review / Revue Internationale de Statistique, 73-79, 1983.
[3] Song, S., Jongwoo S., A note on the history of the gambler’s ruin problem. Communications for Statistical Applications and Methods 20.2, 157-168, 2013.
[4] Ross, S. M., Introduction to probability models. Academic press, 2014.

