Topolojik Uzayların Simetrileri

Yazar: Ergün Yalçın (yalcine@fen.bilkent.edu.tr)

Yıl: 2022-2

Sayı: 112

Topolojik uzaylar

Matematikte üzerinde konuştuğumuz her şeyin iyi tanımlı olmasına özen gösteririz. Bazı daha temel matematiksel kavramları bildiğinizi varsayarak topolojik uzay tanımıyla başlayalım.

Tanım 1.

$X$ bir küme olsun, $P(X)$ de $X$’in altkümelerinin kümesini göstersin. $\mathcal T$ kümesi $P(X)$’in bir altkümesi olsun. Eğer $\mathcal T$ aşağıdaki koşulları sağlıyorsa bu durumda $\mathcal T$ kümesine bir topoloji, $X$’e de bir topolojik uzay diyoruz:

$(i)$ Boş küme $\emptyset$ ve $X$ kümeleri $\mathcal T$’nin içindedir.

$(ii)$ $\mathcal T$’deki kümeler birleşim altında kapalıdır: 

$$\text{Her } \{U_{\alpha} \in \mathcal T \} _{\alpha \in I} \ \text{ için }  \bigcup _{\alpha \in I }  U_{\alpha} \in \mathcal T.$$ 

$(iii)$ $\mathcal T$’deki kümeler sonlu sayıda kümenin kesişimi altında kapalıdır:

$$\text{Her } U_1, U_2, \dots, U_n \in \mathcal T \ \text{ için } \ U_1 \cap \cdots \cap U_n  \in \mathcal T.$$

Topolojik uzayları bazen sadece $X$ ile gösteriyoruz bazen de $(X, \mathcal T)$ şeklinde ikili olarak yazıyoruz. $X$ üzerinde tanımlı topolojiyi $\mathcal T_X$ ile ifade ediyoruz. $\mathcal T_X$’in elemanlarına $X$ kümesinin açık altkümeleri deniyor. Eğer $C\subseteq X$ tümleyeni açık olan bir altküme ise $C$’ye kapalı altküme deniyor. Topolojinin sadece kapalı kümeleri kullanan bir tanımını vermek de mümkün.

Topoloji aslında çevremizdeki geometrik objeleri çalışmak için ortaya çıkmış bir teoridir, ama yaptığımız tanımın genelliğine bakınca geometriyle ilgisi olmayan birçok şeyin de topolojik uzay olabildiğini fark etmişsinizdir.

Örnek 1.

$X=\{1, 2\}$ kümesi üzerinde $\mathcal T=\{ \emptyset , \{1\}, \{1, 2\}\}$ kümesi bir topoloji tanımlar.

Herhangi bir $X$ kümesi için $\mathcal T$ kümesini $X$’in tüm altkümeler kümesi olarak alırsak, o da bir topolojik uzay olur. Bu topolojiye $X$ kümesi üzerinde tanımlı ayrık topoloji denir. Herhangi bir $X$ kümesi için $\mathcal T=\{ \emptyset, X \}$ kümesi de bir topoloji tanımlar. Buna da aşikár topoloji deniyor.

Tanım 2.

Eğer $(X, \mathcal T)$ bir topolojik uzay, $Y$ de $X$’in bir altkümesi ise $Y$ üzerinde bir altuzay topolojisi tanımlayabiliriz. Altuzay topolojisinde açık kümeler kümesi şu şekilde tanımlanır:
$$\mathcal T|_Y= \{ U \cap Y\ |\ U \in \mathcal T \}.$$ Bu kümenin topoloji tanımın üç özelliğini de sağladığını kolaylıkla gösterebilirsiniz. Bu topoloji altındaki $Y$ uzayına $X$ uzayının bir altuzayı denir.

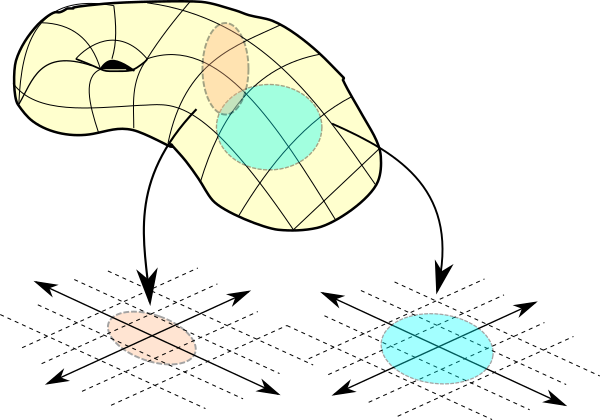
Tabii nihayi amacımız çevremizde gördüğümüz bazı cisimler üzerindeki simetrileri incelemek, ama bunu topolojik uzay genellemesi altında yapmak istiyoruz. Mesela bir topun yüzeyinin topolojik uzay olmasını bekliyoruz, ama topun yüzeyi üzerinde topolojiyi nasıl tanımlayacağımızı düşünmemiz gerekecek. Zira tek tek altkümeler listeleyerek topolojik uzay tanımlamak zahmetli bir iş. Bunu daha sonra metrik uzay tanımıyla yapacağız. Önce topolojik uzaylar için sürekli fonksiyon tanımını yapalım.

Tanım 3.

$f: X \to Y$ iki topolojik uzay arasında bir fonksiyon olsun. Eğer her $U \in \mathcal T_Y$ için $f^{-1} (U) \in \mathcal T _X$ ise $f$ fonksiyonuna sürekli fonksiyon denir.

Matematikçiler genelde bir kategori içinde çalışırlar. Kategori objeleri ve morfizmaları olan bir matematiksel yapıdır. Tabii kategori oluşturabilmesi için morfizmaların bazı aksiyomları sağlaması gerekiyor. Mesela iki morfizmayı art arda uyguladığımızda yeni bir morfizma vermeli. Bir de birim morfizma diye, diğer morfizmalarla birleşince onları geri veren bir morfizmamız olmalı.

Topolojik uzaylar kategorisinin morfizmaları sürekli fonksiyonlardır. Morfizmaları bir kategoride eşyapılı
olma durumunu tanımlamak için kullanıyoruz.

Tanım 4.

$f: X\to Y$ iki topolojik uzay arasında sürekli bir fonksiyon olsun. Eğer $f$’nin fonksiyon olarak tersi varsa ve tersi de sürekliyse bu durumda $f$’ye bir eşyapı dönüşümü (homeomorfizma) denir.
Aralarında eşyapı dönüşümü olan iki uzaya eşyapılı (homeomorfik) diyoruz.

Mesela topolojileri uygun bir şekilde tanımlanırsa bir küp ile bir topun yüzeyi topolojik olarak eşyapılıdır. Bu gözümüze farklı gözüken birçok şeyin topolojik uzay olarak eşyapılı olabileceğine bir örnek. Topoloji, çevremizdeki cisimleri eşyapılı olma denklik bağıntısı altında çalışmamızı sağlıyor. Bazı cisimleri eşyapılı ilan ederek cisimlerin göze farklı gözüken birçok özelliğini yok saymış oluyoruz, bu şekilde onların asıl anlamak istediğimiz özelliklerine odaklanabiliyoruz.

Şimdi bazı iyi bilinen topolojik uzay örneklerini inceleyelim.

1. Metrik Uzaylar: Önce mesafe kavramının tanımını verelim.

Tanım 5.

$X$ bir küme olsun, $d: X \times X \to \mathbb{R}$ de $X\times X$ üzerinde tanımlı reel sayı değerli bir fonksiyon olsun. Eğer $d$ fonksiyonu aşağıdaki koşulları sağlıyorsa $d$’ye $X$ üzerinde tanımlı bir mesafe fonksiyonu ya da metrik denir:

$(i)$ Her $x, y \in X$ için $d(x, y)\geq 0$, ve $$d(x,y)=0 \Leftrightarrow x=y.$$
$(ii)$ Her $x, y \in X$ için $d(x,y)=d(y,x)$.
$(iii)$ Her $x, y, z \in X$ için $d(x,z)\leq d(x,y)+d(y,z)$.

Üzerinde bir metrik tanımlanmış $X$ kümesine metrik uzay diyoruz. Metrik uzaylar çoğunlukla
$(X, d)$ şeklinde ikili olarak ifade ediliyor, ama metrik belliyse bazen sadece $X$ olarak da yazıyoruz.

Bir metrik uzay verildiğinde bu uzayın üzerinde metrik topoloji denen bir topoloji tanımlamak mümkün. Bu topolojiyi açık toplar kullanarak tanımlıyoruz.

Tanım 6.

$(X,d)$ bir metrik uzay olsun. Verilen her $x\in X$ ve $\epsilon >0$ reel sayısı için,
$$B_{\epsilon} (x) =\{ y \in X\ |\ d(x,y) < \epsilon \}$$
altkümesine $x$ merkezli $\epsilon$ yarıçaplı açık top diyoruz. $(X, d)$ üzerindeki,

$$\mathcal T {(X, d)} = \{ U \subseteq X \; \vert \; \text{Her } x \in U \text{ için bir } \epsilon >0 \text{ vardır, } \text{ öyle ki } B_{\epsilon} (x) \subseteq U \}$$

kümesiyle tanımlı topolojiye metrik topoloji deniyor.

Metrik uzayların en bilinen örneği, $n$-boyutlu Öklid uzayıdır. Bu uzayın tanımlandığı küme reel sayıların $n$ kere kendisiyle kartezyen çarpımıdır:
$$\mathbb R^n = \mathbb R \times \cdots \times \mathbb R.$$
$\mathbb R^n$ kümesinde iki nokta arasındaki mesafe şu şekilde tanımlanır:
$$d( (x_1, \dots, x_n), (y_1, \dots, y_n))= \sqrt{\sum _{i=1} ^n (x_i -y_i )^2}.$$
Öklid uzayının altkümeleri üzerinde altuzay topolojisi tanımlayabiliriz.
Mesela 3-boyutlu uzayın içinde oturan kenar uzunlukları 1 olan küpü, yani
$$C^3= [0,1]\times [0,1]\times [0,1]$$
kümesini, bu şekilde bir topolojik uzay olarak görüyoruz.

2. Çokkatlılar:

$X$ bir topolojik uzay olsun. Verilen bir $x\in X$ noktasını içeren açık kümeye, $x$ noktasının bir (açık) komşuluğu diyoruz. Eğer $X$ uzayının içindeki her $x\in X$ noktasının çevresinde $n$-boyutlu Öklid uzayının bir altuzayına eşyapılı bir komşuluk bulabiliyorsak $X$ uzayına $n$-boyutlu topolojik çokkatlı (manifold) denir. Aslında çokkatlı tanımında uzayın Hausdorff ve tümden sayılabilir de olması lazım, ama bu kavramları burada açıklamayacağız.

Örnek 2.

$(n+1)$-boyutlu Öklid uzayının içindeki birim küre,
$$ S^n =\{ (x_0, \dots, x_n ) \in \mathbb{R}^{n+1} \, | \, \sum _{i=0} ^n x_i ^2=1 \}$$
$n$-boyutlu bir çokkatlıdır.

$n$-boyutlu kürenin neden bir topolojik çokkatlı olduğu topoloji derslerinin standart sorularından biridir.
İspatı genelde kürenin üzerinde $U=S^n \backslash { (0, \dots, 0, 1)}$ ve $V=S^n \backslash { (0, \dots, 0, -1)}$ açık kümeleri alınarak yapılır. Bu açık kümelerin $n$-boyutlu Öklid uzayının bir altkümesiyle eşyapılı olduklarını göstermeyi okuyuculara bırakıyorum. Ama iki boyutlu kürenin bir çokkatlı olduğuna en iyi kanıt dünyanın düz olduğunu iddia eden insanların varlığıdır herhalde.

3. Simpleksel kompleksler:

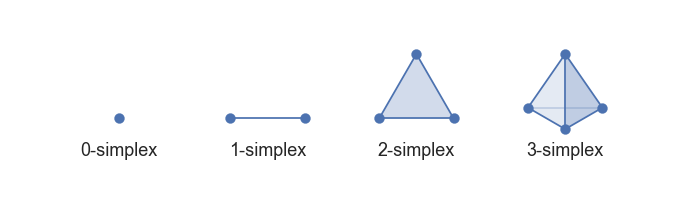
$(n+1)$-boyutlu Öklid uzayının aşağıdaki şekilde tanımlanan altuzayına $n$-simpleks deniyor: $$\Delta ^n =\{ (x_0, \dots, x_n ) \in \mathbb{R}^{n+1} \, | \, x_i \geq 0,\ \sum _{i=0} ^n x_i =1 \}$$
$0$-simpleks $\Delta ^0$ sadece bir noktadan oluşuyor, $\Delta ^1$ ise iki nokta arasına bir çizgidir. $\Delta ^2$ içi dolu bir üçgen, $\Delta ^3$ ise içi dolu bir düzgün dörtyüzlü olarak düşünülebilinir.

Bir $n$-simpleksin dış yüzeyi $\partial \Delta ^n$ ile ifade edilir ve topolojik olarak $(n-1)$-boyutlu küreyle eşyapılıdır. $\partial \Delta ^n$ daha küçük boyutlu simplekslerden oluşur. Mesela bir $2$-simpleksin dış yüzeyi bir üçgendir ve üç tane $1$-simpleksin uç noktalarından yapıştırılmasıyla elde edilir. Aynı şekilde bir $3$-simpleksin dış yüzeyi dört tane $2$-simpleksin kenarları boyunca yapıştırılmasıyla elde edilir.

Bir simpleksin dış yüzeyindeki daha küçük boyutlu simplekslere o simpleksin yüzleri denir. Bir $n$-simpleksin yüzleri, $0 \leq k\leq n-1$ olacak şekilde, $k$-boyutlu simplekslerdir.

Tanım 7.

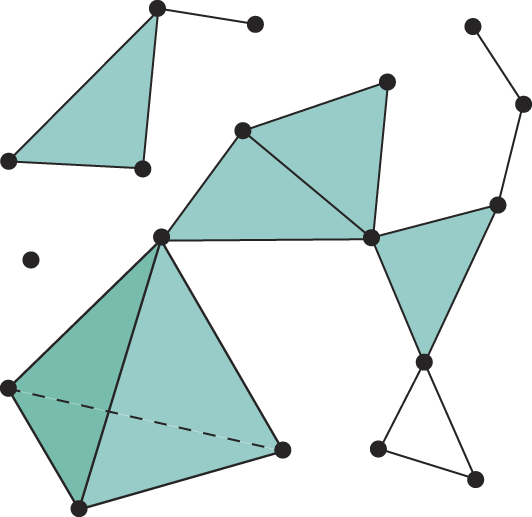
Simpleksleri yapıştırarak elde edilen uzaylara simpleksel kompleks diyoruz. Burada yapıştırma için kural şu: iki simpleksi sadece yüzleri boyunca yapıştırmaya izin veriliyor.

Eğer $X$ bir topolojik uzay, $K$ de $X$ ile topolojik olarak eşyapılı bir simpleksel kompleks ise
$K$ simpleksel kompleksine $X$ uzayının bir üçgenlemesi denir. Mesela $\partial \Delta ^n$ simpleksel kompleksi $(n-1)$-boyutlu kürenin bir üçgenlemesidir. $n=2$ için bu üçgenleme bir çemberi bir üçgen olarak düşünmeye tekabül eder, $n=3$ için de iki boyutlu küreyi bir düzgün dörtyüzlünün dış yüzeyi olarak görmek anlamına gelir.

Üçgenlemelere başka bir örnek de şu: Bir karenin çevresi dört çizgiden oluşur. Bu çizgilerin her birini bir 1-simpleks olarak düşünürsek, bu bize çemberle eşyapılı olan bir simpleksel kompleks verir. Dolayısıyla bir çemberi üçgenlemenin birden fazla yolu vardır. Verilen her $n$-sayısı için çemberin $n$-tane 1-simpleksten oluşan üçgenlemesi verilebilir. Bu üçgenlemeyi çemberi bir $n$-gon olarak düşünerek yapıyoruz. Bu üçgenlemeler topolojik uzayların simetrilerini bulurken bize çok yardımcı oluyor.

Makalemizin son bölümünde homotopi kavramı da zaman zaman geçecek. Homotopinin tanımını burada vermeyeceğiz. Bu tanımı cebirsel topoloji kitaplarında bulabilirsiniz. Genel olarak topolojik uzaylar konusunda daha detaylı bilgileri şu kitaplarda bulabilirsiniz: [10], [9], [7], [13]

Simetri grupları

Topolojik uzayların simetrilerini incelemek için öncelikle simetri kavramını matematiksel olarak tanımlamamız gerekiyor. Bunu yapmanın yolu simetrileri bir matematiksel yapı olan grupları kullanarak ifade etmek. Grubun tanımını vermeden önce işlem neye denir onu tanımlayalım.

$G$ bir küme olsun. $G\times G$ kümesinden $G$’ye giden fonksiyonlara $G$ üzerinde tanımlı bir işlem diyoruz. Bu işlemi her $g, h\in G$ için, $$(g, h) \to g\ast h$$ ile gösterelim. Üzerinde $\ast$ işlemi tanımlı $G$ kümesini $(G, \ast)$ ikilisi olarak ifade ediyoruz.

Tanım 8.

$(G, \ast)$ üzerinde işlem tanımlı bir küme olsun. $\ast$ işlemi aşağıdaki koşulları sağlıyorsa, $(G, \ast)$ ikilisine grup denir:

$(i)$ Her $g,h,k\in G$ için $(g\ast h) \ast k=g\ast (h\ast k).$
$(ii)$ $G$’de birim eleman vardır: $G$’de $1$ olarak gösterilen aşağıdaki koşulu sağlayan bir eleman vardır:
Her $g\in G$ için, $$1\ast g=g=g \ast1.$$
$(iii)$ Her $g\in G$ için $g^{-1}$ diye bir eleman vardır, öyle ki $$g\ast g^{-1}=1=g^{-1} \ast g.$$
Bu elemana $g$’nin ters elemanı denir.

Daha önce yaptığımız gibi bir grubu bazen sadece $G$ ile ifade ediyoruz bazen de işlemiyle beraber,
$(G, \ast)$, $(G, +)$, $(G, \cdot)$ şeklinde ikililer olarak yazıyoruz. Kolaylık olsun diye bütün gruplarda grup işlemini $g\cdot h$ ya da sadece $gh$ diye yazıyoruz.

Örnek 3.

Tamsayılar kümesi $\mathbb Z=\{0, \pm 1, \pm 2, \cdots\}$ toplama işlemi altında bir grup olur. Birim eleman $0$ sayısıdır. $n \in \mathbb Z$ tamsayısının ters elemanı $-n$ tamsayısıdır.

Örnek 4.

$C_2=\{ +1, -1\}$ kümesi tamsayılardaki çarpma işlemi altında bir grup oluşturur. Bu grubun birim elemanı $1$’dir ve her elemanın tersi kendisidir.

Yukarıdaki örneklerde gördüğünüz gibi grupların sonlu sayıda ya da sonsuz sayıda elemanı olabilir. Sonlu sayıda elemanı olan gruplara sonlu grup denir. Bazı grupların üzerinde grup yapısıyla uyumlu bir topoloji tanımlanabilir. Bu tür gruplara topolojik grup denir. Bunun en basit örneği çember grubudur.

Örnek 5.

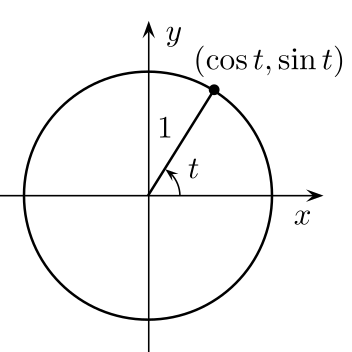
$S^1=\{ z\in \mathbb C \ | \ |z|=1\}$ uzunluğu 1 olan kompleks sayılar kümesini göstersin. Kompleks sayı çarpması altında bu küme bir grup oluşturur. Burada çarpma işlemi $S^1 \times S^1\to S^1$ ve ters alma fonksiyonları $S^1 \to S^1$ sürekli işlemlerdir. Çember üzerinde tanımlı topolojiyi 2-boyutlu Öklid uzayının altküme topolojisi olarak, $S^1\times S^1$ üzerindeki topolojiyi de çarpım topolojisi olarak alıyoruz. Çarpım topolojisini tanımlamadık, ama bu topolojinin tanımını topoloji kitaplarında bulmak mümkün [10, $\S$ I.2.29]

$G$ bir grup olsun, $H \subseteq G$ de $G$ grubunun boş olmayan bir altkümesi olsun. Eğer $H$ kümesinin elemanları $G$’deki işleme tabi tutulduğunda $H$ kümesinin içinde kalıyorsa ve $H$ kümesindeki elemanların tersi $H$ kümesinde oturuyorsa, bu durumda $H$ kümesi $G$ grubunun işlemi altında bir grup oluşturur. Bu şeklide oluşan gruplara $G$ grubunun altgrubu diyoruz. Mesela çift tamsayılar kümesi tamsayılar grubunun bir altgrubudur. Bu altgrup genellikle $2\mathbb Z$ ile gösterilir.

En çok karşılaştığımız gruplardan biri de devirli sonlu gruplardır. Bu grupları $S^1$ çember grubunun altgrupları olarak tanımlayabiliriz.

Örnek 6.

Verilen $n\geq 1$ tamsayısı için,
$$C_n :=\{ z\in S^1 \, | \, z^n=1 \}$$
kümesi kompleks sayıların çarpması altında bir grup oluşturur.
Bu grubun elemanları,
$$\{ e^{2\pi i/n} \, | \, i=0,\dots, n-1 \}$$ kümesidir. Bu gruba $n$ elemanlı devirli grup denir.

Devirli grupları grupların üreteçli gösterimini kullanarak şu şekilde de ifade ediyoruz:
$$C_n =\langle g \ | \ g^n=1 \rangle.$$
Grup gösterimleri grupları tanımlamanın kullanışlı bir yöntemidir. Mesela çok sık karşılaştığımız
gruplardan biri olan dihedral gruplar grup gösterimi verilerek şu şekilde tanımlanır:

Tanım 9.

Her $n \geq 2$ tam sayısı için,
$$D_{2n}:=\langle r, s\ |\ r^n=s^2=1, srs=r^{-1} \rangle$$
eleman sayısı $2n$ olan dihedral grubu tanımlar. Bu grubun elemanları liste olarak şu şekildedir:
$$D_{2n}=\{1, r, r^2, \dots, r^{n-1}, s, sr, \dots, sr^{n-1} \}.$$

Verilen iki grup arasında grup işlemlerini koruyan $f: G\to H$ fonksiyonlarına grup homomorfizması denir. Grup işlemini korumaktan kastımız her $g_1, g_2\in G$ için $f(g_1 g_2)=f(g_2)f(g_2)$ eşitliğinin sağlanmasıdır. Eğer $f: G\to H$ tersi olan bir fonksiyon ise $f$’ye bir eşyapı dönüşümü diyoruz. Aralarında eşyapı dönüşümü olan gruplara eşyapılı (izomorfik) denir ve bu durum $G \cong H$ ile gösterilir.

Örnek 7.

$n$ sayısı $2$’den büyük bir tamsayı olsun. Verilen iki $a, b$ tamsayılarının arasındaki fark $n$ ile bölünüyorsa, $a$ ve $b$ sayıları $n$ modunda denktir diyoruz ve bunu $a \equiv b\ (\text{mod}\ n)$ ile gösteriyoruz. Bu denklik bağıntısı altındaki denklik sınıflarını, $$\mathbb Z/n :=\{ \overline 0, \overline 1, \dots, \overline{(n-1)} \}$$
ile gösterelim. Bu küme üzerinde toplama işlemini şöyle tanımlayabiliriz:
$$\overline a +\overline b=\overline{a+b}.$$ Bu toplama işlemi altında $\mathbb Z/n$ kümesi $n$ elemanlı bir grup oluşturur. Bu grup yukarıda tanımladığımız $C_n$ grubu ile eşyapılıdır. Burada eşyapı dönüşümü $f : \mathbb Z /n \to C_n$ her $\overline a \in \mathbb Z$ elemanı için $f(\overline a)=e^{2a \pi i/n}$ olarak tanımlanır.

Bazen bu kartezyen çarpım grupları başka gruplarla eşyapılı olabiliyor. Mesela verilen iki grubun kartezyen çarpımı $G\times H$ koordinatlarda tanımlı $(g, h) (g’, h’)=(gg’, hh’)$ işlemi altında bir grup oluşturur. $\mathbb Z/2\times \mathbb Z/3$ çarpım grubu $\mathbb Z/6$ devirli grubuyla eşyapılıdır.

Grupların ortaya çıkışı aslında matematiksel yapıların simetri grupları olarak olmuştur. Grubun soyut tanımı daha sonra veriliyor. O yüzden soyut grup tanımını daha iyi anlamak için simetri grubu kavramını bilmek önemli.

Tanım 10.

$X$ üzerinde bir matematiksel yapı olan bir küme olsun. Bu yapıyı koruyan, tersi olan ve tersi de bu yapıyı koruyan, $f: X \to X$ şeklindeki fonksiyonlara $X$’in simetrisi denir. $X$’in bütün simetrileri birleşim işlemi altında bir grup oluşturur. Bu gruba $X$’in simetri grubu denir ve $Sym(X)$ ile gösterilir.

Örnek 8.

$X$ bir küme olsun. $X$’ten $X$’e tanımlı tersi olan fonksiyonlara $X$ kümesinin bir permütasyonu denir. İki permütasyonun birleşimi yine bir permütasyondur. $Sym(X)$ grubu $X$’in bütün permütasyonlarının oluşturduğu gruptur. $X=\{1, 2, \dots, n\}$ olduğunda $Sym(X)$ grubunu $S_n$ ile gösteriyoruz ve bu gruplara kısaca simetri grupları diyoruz. $S_n$ simetri grubunun eleman sayısı $n! := n \cdot (n-1)\cdots 2\cdot1$’dir. Mesela $S_3$ simetri grubunun $6$ elemanı vardır. Bu grubun elemanlarını permütasyon notasyonu kullanarak şöyle listeleyebiliriz:

$$S_3=\{ 1, (12), (13), (23), (123), (132)\}.$$
Burada $(12)$ demek $1$ ile $2$ yer değiştiriyor, $3$ sabit kalıyor demek. $(123)$ ise $1$ sayısı $2$’ye, $2$ sayısı $3$’e, $3$ sayısı da $1$’e gidiyor demek.

Şimdi katı cisimlerin simetri gruplarını incelerken karşımıza çıkacak başka bir grubu tanımlayacağız. Bu grubu $S_n$ simetri grubunun bir altgrubu olarak tanımlıyoruz.

Örnek. 9

$\sigma: \{ 1,\dots, n\} \to \{1, \dots, n\}$ bir permütasyon olsun. Eğer $i, j \in \{ 1, \dots, n\}$ ikilisi $i \sigma (j)$ koşulunu sağlıyorsa, bu ikiliye kötü ikili diyoruz. Bir permütasyonun içindeki kötü ikili sayısı çift ya da tek sayı olabilir. Bu sayı çiftse o permütasyona çift permütasyon diyoruz. $S_n$ grubunun içindeki çift permütasyonlar birleşim işlemi altında bir altgrup oluşturur. Bu altgruba alterne grup denir ve $A_n$ ile gösterilir. Mesela $A_3$ grubunun elemanları şu şekilde listelenebilir:
$$A_3=\{1, (123), (132)\}$$
Buradan kolayca görülebileceği üzere $A_3$ grubu $C_3$ devirli grubu ile eşyapılıdır. $A_4$ grubu 12 elemanlı bir gruptur:

$$A_4=\{ 1, (12)(34), (13)(24), (14)(23), (123), \
(132), (124), (142), (134), (143), (234), (243)\}$$

Simetri gruplarına en iyi örnekler doğrusal cebirden gelir.

Örnek 10.

Her $n\geq 1$ pozitif tamsayısı için tersi olan $n\times n$ reel matrisler matris çarpması altında bir grup oluştururlar. Bu grubu $GL_n(\mathbb R)$ ile gösteriyoruz. Bu grubun birim elemanı $I_n$ birim matrisidir. Eğer $V$ $n$-boyutlu bir reel vektör uzayıysa, bu durumda $V$’nin vektör uzayı olarak simetri grubu $GL_n(\mathbb R)$ grubuyla eşyapılıdır. $V$ uzayının simetrilerini $GL_n(\mathbb R)$ grubunun elemanları olarak ifade etmek için $V$ vektör uzayının bir tabanını seçeriz. $Sym(V)\cong GL_n(\mathbb R)$ eşyapı dönüşümü seçilen tabana bağlıdır.

Örnek 11.

Eğer $V$ bir iç çarpım uzayı ise bu durumda $V$’nin iç çarpım uzayı olarak simetri grubu,
$$O(n) :=\{ A \in GL_n(\mathbb R) \, | \, A A^T=I_n \}$$
matris grubuyla eşyapılı olur. Eğer $V$’yi $n$-boyutlu Öklid iç çarpım uzayı olarak alırsak, bu durumda simetriler $O(n)$ grubunun elemanları olan matrislerle çarpma olarak tanımlanır. Bu dönüşümler mesafe koruyan doğrusal dönüşümlerdir.

Örnek 12.

Eğer $V$ bir yönlendirilmiş iç çarpım uzayı ise, bu durumda simetri grubu, $$SO(n) =\{ A \in O(n) \, | \, det(A)=1 \}$$ ile eşyapılı olur. Bu altgrubun elemanları bir eksen etrafında döndürme dönüşümleri olarak ifade edilebilir. O yüzden $SO(n)$’nin elemanlardan elde edilen simetrilere döndürme simetrileri diyoruz.

Yukarıda tanımladığımız gruplardan $GL_n (\mathbb{R} )$ bir Lie grubudur, $O(n)$ ve $SO(n)$ ise kompakt Lie gruplarıdır. Lie grupları, aynı zamanda türevlenebilir çokkatlı yapısına sahip olan topolojik gruplardır. Gruplar ve Lie gruplarıyla ilgili daha detaylı bilgiyi şu kitaplarda bulabilirsiniz: [14],[6], [15], [3]

Katı cisimlerin simetri grupları

Üç boyutlu uzay içinde oturan geometrik cisimlere katı cisim diyeceğiz (aslında herhangi bir altküme de olabilir).

Tanım 11.

Üç boyutlu uzayın mesafe koruyan dönüşümlerinden birini uyguladığımızda bir katı cisim kendisine gidiyorsa, o zaman bu dünüşüme o katı cismin simetrisi diyoruz.

Biz sonlu simetri gruplarıyla ilgilendiğimiz için bir koşul daha koyacağız. Bu simetrilerin cismin bir noktasını sabitlediğini varsayacağız. Bu noktayı orijin noktası alıp 3-boyutlu uzayın sadece doğrusal dönüşümlerine odaklanacağız. Üç boyutlu uzayın mesafe koruyan doğrusal dönüşüm grubu $O(n)$ matris grubudur. Dolayısıyla her katı cismin simetri grubu $O(n)$ grubunun bir altgrubu olacak.

Örnek 13.

Bir ikizkenar üçgen alalım. Bu üçgeni, ağırlık merkezi orijinde olacak şekilde, üç boyutlu uzayın içine oturtalım. Bu şekilde oturan bir üçgenin birim simetri dışında sadece bir simetrisi vardır. Eşit kenarlarını birbirine götürebilirsiniz. Bu simetriyi veren dönüşümü tekrar uygularsanız birim simetri elde edersiniz.
Bu bize ikizkenar üçgenin simetri grubunun $C_2=\{ +1, -1\}$ grubuyla eşyapılı olduğunu söyler.

Örnek 14.

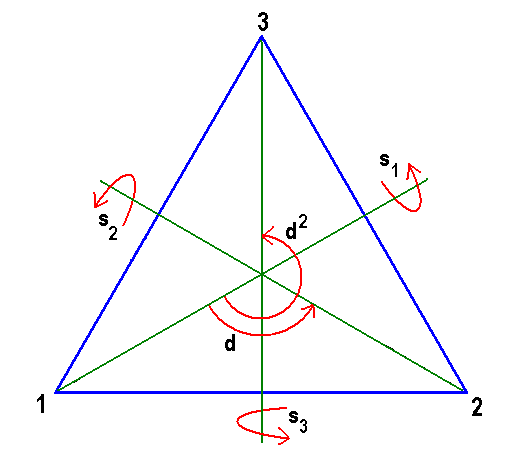
İkizkenar üçgen yerine bir eşkenar üçgen alırsak simetrilerinin sayısı artacaktır. Aşağıdaki şekilde bir eşkenar üçgenin bütün simetrilerini görüyorsunuz.

Eşkenar üçgenin birim simetri ile beraber toplam 6 simetrisi vardır ve simetri grubu $S_3$ simetri grubuyla eşyapılıdır. Bunu görebilmek için eşkenar üçgenin simetri grubuna $G$ diyelim ve bir $f: G \to S_3$ grup homomorfizması tanımlayalım. $f$, üçgenin simetrilerini, bu simetrinin köşe noktaları kümesi $\{1, 2, 3\}$ üzerinde yarattığı permütasyona götüren homomorfizma olsun. Bu şekilde tanımlanan $f$ homomorfizması Görsel 4’te gösterilen $s_2$ simetrisini $S_3$ grubundaki $(13)$ elemanına, $d$ simetrisini de $(123)$’e götürür. $S_3$ grubunun tüm elemanlarının üçgenin bir simetrisi tarafından elde edilebileceğini Görsel 4’te gösterilen simetrilerden kolayca görebilirsiniz. Bu bize $f$’nin örten bir fonksiyon olduğunu söylüyor. Üçgenin bütün köşelerini sabitleyen dönüşüm birim dönüşümdür. Buradan $f$’nin birebir, dolayısıyla da bir eşyapı dönüşümü olduğunu görüyoruz. Sonuç olarak bir eşkenar üçgenin simetri grubu $S_3$ grubuyla eşyapılıdır.

Yukarıda eşkenar üçgenin tüm simetrilerini bulurken bir ayrım yapmadan hepsini dahil ettik, ama bu simetrilere dikkatli bakarsanız bazıları yansıma işlemiyle elde edilirken, bazıları döndürme ile elde edilmiştir. Eşkenar üçgenin sadece döndürme simetrileri yani $SO(3)$ grubundan gelen simetri-leri bütün simetri grubunun içinde bir altgrup oluşturur. Eşkenar üçgenin döndürme simetri grubu $A_3 \cong C_3$ grubu ile eşyapılıdır.

Birçok katı cismin simetri grubu buna benzer bir şekilde hesaplanabilir. Mesela yukarıda yaptığımız hesabı tüm kenarları eşit uzunlukta olan bir $n$-gon için yapsaydık simetri grubunun $2n$ elemanlı
$D_{2n}$ dihedral grubu olduğunu görecektik.

Teorem 1.

Her $n\geq 3$ tamsayısı için merkezi orijinde olacak şekilde üç boyutlu uzay içinde oturan $n$ köşeli bir çokgenin tüm simetrilerinin grubu, $D_{2n}$ dihedral grubudur. Çokgenin döndürme simetri grubu $C_n$ devirli grubudur.

Aslında üçgen için bulduğumuz simetri grubu bu genel hesabın bir özel bir durumu, çünkü $S_3$ simetri grubuyla dihedral grup $D_6$ eşyapılıdır.

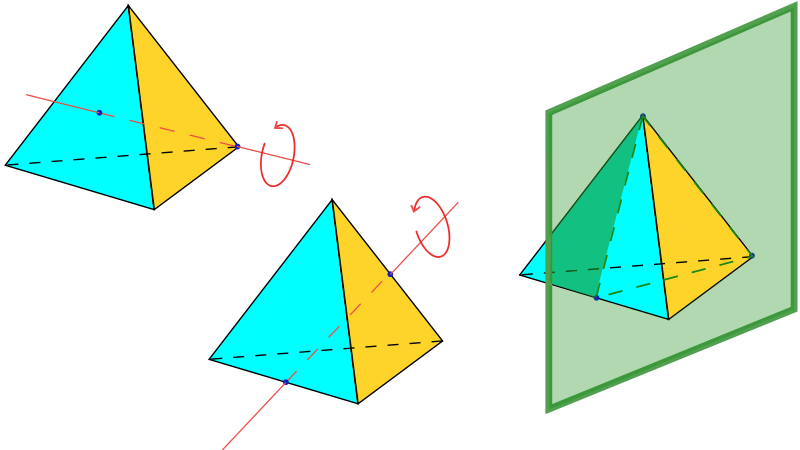
Şimdi düzgün dörtyüzlünün simetri grubunu hesaplayalım. Aşağıdaki görselde düzgün dörtyüzlünün bazı simetrilerini görüyorsunuz.

Düzgün dörtyüzlünün simetri grupları için iddiamız şu:

Teorem 2.

Düzgün dörtyüzlünün tüm simetri grubu $S_4$ simetri grubudur ve döndürme simetri grubu $A_4$ alterne grubudur.

Kanıt. Bütün kenarları eşit uzunlukta olan bir düzgün dörtyüzlü alalım ve ağırlık merkezi orijinde olacak şekilde üç boyutlu uzayın içinde oturduğunu varsayalım. Bu katı cismi simpleks notasyonundan esinlenerek $\Delta ^3$ ile gösterelim. $\Delta ^3$’ün bütün köşelerini $\{ 1, 2, 3, 4\}$ olarak numaralandıralım. $$f: Sym (\Delta ^3) \to S_4$$ grup homomorfizmasını $\Delta ^3$’ün simetrilerini bu simetrilerin köşe noktaları üzerinde yarattığı permütasyonuna götüren fonksiyon olsun.

$S_3$ grubunun tüm elemanları $(i \ j)$ şeklindeki elemanların çarpımı olarak ifade edilebilir. Buradan $f$’nin örten olduğunu görüyoruz. $f$ dönüşümünün birebir olduğunu göstermek için şu gözlemi yapalım. Eğer $A, B \in O(n)$ dönüşümleri $f$ altında aynı permütasyona giden iki dönüşümse, bu durumda $f(A^{-1} B)$ birim permütasyon olacağı için $A^{-1} B$ dönüşümü $\Delta ^3$’ün bütün köşelerini sabitler. $\Delta^3$’ün üç köşesi doğrusal bağımsız üç vektör verir ve $O(3)$’te doğrusal bağımsız üç vektörü sabitleyen tek dönüşüm birim dönüşümdür. Buradan $A^{-1} B=I_3$ elde ederiz, yani $A=B$ olur. Sonuç olarak $f$ bir eşyapı dönüşümüdür ve $Sym (\Delta ^3)$ grubu $S_4$ simetri grubuyla eşyapılıdır.

Düzgün dörtyüzlünün sadece döndürme simetrilerine odaklanırsak $(12)$ gibi permütasyonların artık döndürme simetrileriyle elde edilemediğini görürüz. Döndürmelerle elde edebildiğimiz simetriler tüm simetri grubu içinde indeksi 2 olan bir altgrup oluşturur (yani $H$ bu altgrupsa $H$’nin eleman sayısı 12 olmalıdır). Grup teori kullanarak $S_4$ grubunun indeksi iki olan sadece bir altgrubu olduğunu ve bu altgrubun $A_4$ alterne grubu oldugunu gösterebiliriz. Görsel 5’teki şekile dikkatlice bakarsanız, $A_4$ altgrubunun bütün elemanlarının düzgün dörtyüzlüyü belirli bir eksen etrafında döndürerek elde edilebildiğini görebilirsiniz. Bu bize düzgün dörtyüzlünün döndürme simetri grubunun $A_4$ alterne grubu olduğunu gösterir.

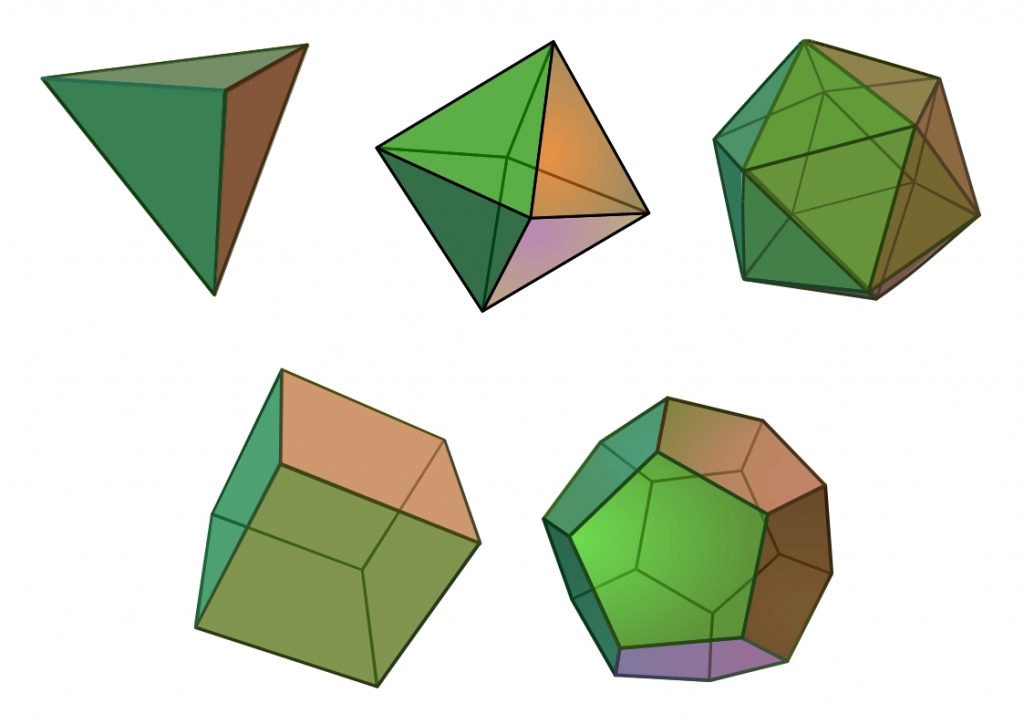
Yukarıda yaptığımız hesabın benzerlerini diğer düzgün çokyüzlüler için de yapabiliriz. Eski çağ-lar-dan
beri bilindiği üzere tam beş tane konveks düzgün çokyüzlü vardır. Bu düzgün çokyüzlüler ingilizce adlarıyla Tetrahedron (dörtyüzlü), cube (küp), octahedron (sekizyüzlü), dodecahedron (onikiyüzlü) ve icosahedron (yirmiyüzlü)olarak adlandırılır.

Düzgün çokyüzlülerden küp ve sekizyüzlü birbirlerinin dualidir. Aynı şekilde onikiyüzlü ile yirmiyüzlü de birbirleriyle dualdir. Birbirlerine dual düzgün çokyüzlülerin simetri grupları birbirleriyle eşyapılıdır. Düzgün çokyüzlülerin döndürme simetri grupları şunlardır:

Teorem 3.

Düzgün dörtyüzlü, küp/sekizyüzlü, onikiyüzlü/yirmiyüzlü çokyüzlülerinin döndürme simetri grupları sırasıyla $A_4$, $S_4$, ve $A_5$ gruplarıdır.

Düzgün dörtyüzlü için hesabı yukarıda yapmıştık. Küp ve sekizyüzlü için döndürme simetri grubunun
$S_4$ olduğu benzer bir yöntemle gösterilebilir. Küp için, sekiz köşeden üstekiler $\{1,2, 3,4\}$ olarak, alttakiler de $\{1′, 2′, 3′, 4’\}$ olarak numaralandırılır. $k$ ile numaralandırılan köşenin köşegen boyunca karşısındaki köşe $k’$ ile numaralandırılır. Küpün simetrileri İpek Tuvay’in derginin bu sayısında bulabileceğiniz makalesinde detaylı olarak inceleniyor. Onikiyüzlü/yirmiyüzlü için hesap biraz daha karışık. Hesap onikiyüzlü içerisine beş tane küp yerleştirerek yapılıyor. Döndürme simetrilerini bulduktan sonra tüm simetri gruplarını bulmak için yansıma simetrilerini de inceliyoruz. Sonuç olarak şunu elde ediyoruz:

Teorem 4.

Düzgün dörtyüzlü, küp/sekizyüzlü, onikiyüzlü/yirmiyüzlü çokyüzlülerinin tüm simetri grupları sırasıyla $S_4$, $C_2 \times S_4$, ve $C_2 \times A_5$ gruplarıdır.

Bu simetri gruplarının hesabını simetriler üzerine yazılmış bazı kitaplarda bulabilirsiniz ([ 2, Chp.
8], [ 4, Chp 2, Lect 12]). Ayrıca internette bu konuda yazılmış kısa öğrenci raporları ve ders notları bulmak da mümkün ([11], [12]).

Bu bölümü sonlandırmadan önce sonlu döndürme gruplarıyla ilgili şu teoremi de burada ifade etmekte fayda var.

Teorem 5.

$SO(3)$ grubunun sonlu altgrupları ya düzgün çokyüzlülerin simetri gruplarından biridir (yani $A_4$, $S_4$, veya $A_5$) ya da devirli grup $C_n$ veya dihedral grup $D_{2n}$’dir.

Bu teorem Armstrong’un kitabında Teorem 19.2 olarak ispatlanıyor [2].

Climenhaga ve Katok’un kitabında ise Teorem 2.36 olarak ispatlanmış [4]. Bu teoremin ispatı bir lisans öğrencisinin anlayabileceği düzeyde.

Kürelerin sonlu grup simetrileri

Bu son bölümde kürelerin topolojik uzay olarak sonlu grup simetrilerinden bahsedeceğiz. Topolojik uzaylar için simetri kavramı, üzerinde yapı olan bütün diğer kümeler için yaptığımız tanımla aynı. Her $X$ topolojik uzayı için $f:X\to X$ şeklindeki, tersi olan, tersi de sürekli olan, fonksiyonlara $X$ uzayının bir simetrisi diyoruz. Bir topolojik uzayın simetri grubunu $Homeo(X)$ ile gösterilir. $X$ uzayı bazı koşulları sağlıyorsa $Homeo(X)$ bir topolojik grup oluyor. Genelde bu grup çok büyük bir grup, sadece bazı denklik bağıntıları altında çalışılıyor. Mesela yüzeyler için $Homeo(X)$ yerine onun bir kesir grubu olan eşleme sınıfı grupları (mapping class group) çalışılıyor.

Biz bu yazıda dikkatimizi $Homeo(X)$ grubunun içindeki sonlu altgruplara vereceğiz. Bu tür sonlu gruplar, $X$ uzayı üzerine etki ederler. Bir grubun bir topolojik uzay üzerindeki etkisinin tanımı tam olarak şöyle veriliyor:

Tanım 12.

$X$ topolojik bir uzay, $G$ de sonlu bir grup olsun. Eğer,

$$G \times X\to X$$

$$(g,x) \to gx$$

şeklinde sürekli bir fonksiyon varsa, öyle ki

$(i)$ her $g, h\in G$ ve her $x\in X$ için $(gh) x=g(hx) $;
$(ii)$ her $x\in X$ için $1x=x$;
olsun, bu durumda $G$ grubunun $X$ uzayı üzerinde grup etkisi vardır diyoruz.

Örnek 15.

$G=C_2=\langle t \, | \, t^2=1 \rangle$ ve $X=S^n$ uzayı $n$ boyutlu küre olsun.

$G\times X \to X$ grup etkisini, $$t(x_0 , \dots , x_n ) = (-x_0, \dots, -x_n )$$ ile tanımlayalım. Bu etkiye ters kutup etkisi (antipodal etki) deniyor. Bu etki küre üzerinde hiçbir noktayı sabitlemez, her nokta kendinden başka bir noktaya gider.

Örnek 16.

$G=S^1$ çember grubu ve $$S^2 =\{ (x,y,z) \in \mathbb R ^3 \, | \, x^2+y^2+z^2=1\}$$
iki boyutlu küre olsun. Çember grubunun elemanlarını $0 \leq \theta \leq 1$ olacak şekilde kutupsal formda,
$$z(\theta)=\cos (2\pi \theta)+i \sin (2 \pi \theta) $$ olarak ifade edebiliriz. Çember grubunun iki boyutlu küre $S^2$ üzerindeki grup etkisini,
$$z(\theta) \cdot (x,y,z)= (x \cos (2\pi \theta) , y \sin (2\pi \theta), z)$$
olarak tanımlayalım. Bu etki küreyi kuzey ve güney kutuplarından geçen eksen etrafında döndürme etkisidir. Bunu bir topacın dönmesine benzetebiliriz. Bu etki altında kuzey ve güney kutupları sabit kalır.

Tanım 13.

$X$ üzerinde $G$ etkisi olan bir topolojik uzay olsun. Eğer her $g \in G$ ve $x \in X$ için,
$$(gx=x) \implies (g=1)$$ koşulu sağlanıyorsa bu etkiye serbest etki diyoruz.

Yukarıda verdiğimiz birinci örnekteki ters kutup etkisi serbest bir etkidir. İkinci tanımladığımız etkiyse kutupları sabit bıraktığı için serbest değildir. Serbest olmayan etkilere başka bir örnek de yansımayla tanımlanan etkilerdir.

Örnek 17.

$G=C_2=\langle t \, | \, t^2=1 \rangle$ ve $X=S^n$ olsun. $G\times X \to X$ etkisini,
$$t (x_0, \dots, x_{n-1}, x_n)=(x_0, \dots, x_{n-1}, -x_n )$$ olarak tanımlayalım. Bu bir yansıma etkisidir ve ekvator bu etki altında sabit kaldığı için serbest bir etki değildir.

Serbest olmayan etkileri daha iyi anlamak için noktaların izotropi gruplarına bakılır. Üzerinde $G$ etkisi olan bir $X$ topolojik uzayındaki $x \in X$ noktasının izotropi altgrubu,
$$G_x =\{ g \in G \, | \, gx=x \}$$
olarak tanımlanıyor. Serbest etkiler $X$ uzayının her noktasında izotropinin aşikâr altgruba eşit
olduğu etkilerdir. Serbest etkilerle ilgili şu soruyu sorabiliriz:

Soru 1.

Hangi sonlu gruplar bir küreye (herhangi bir boyutta) serbest olarak etki edebilir?

Bu problemin kürelerin boyutlarını sabit tutan versiyonuna topolojik küresel uzay formu problemi deniyor. Bu problem dönüşüm grupları (grup etkileri) çalışma alanının en önemli problemlerinden biridir. Problemin yukarıdaki versiyonu birçok matematikçinin uzun yıllar süren çabaları sonucunda en sonunda 80’li yıllarda çözülmüştür. Çözüm bu tür etkilere sahip grupların önce bütün özelliklerinin bulunması daha sonra da bu grupların bir listesinin verilmesiyle sonuçlanmıştır. Bu tür teoremlere sınıflandırma teoremi diyoruz.

Bu önemli sınıflandırma teoremini anlatmadan önce sonlu döndürme gruplarıyla ilgili bazı şeyleri hatırlayalım. $O(n)$ grubu $n$-boyutlu Öklid uzayına mesafe koruyacak şekilde etki ettiği için
$(n-1)$-boyutlu küreye doğal olarak etki eder. Bu şekilde elde edilen etkilere ortogonal temsillerden gelen etkiler diyeceğiz. Mesela $SO(3)$ grubunun sonlu altgrupları iki boyutlu küreye bu şekilde etki ederler.

$SO(3)$ grubunun sonlu altgruplarının iki boyutlu küreye etkilerini daha iyi görebilmek için kürenin içine bir düzgün çokyüzlü yerleştirip küre üzerindeki noktalarla bu çokyüzlünün noktalarını eşliyoruz. Burada yaptığımız şey aslında küreyi çokyüzlüleri kullanarak üçgenlemek (bazı yüzleri daha küçük üçgenlere bölmek gerekebiliyor). $SO(3)$’ün elemanları üç boyutlu uzaya bir eksen etrafında döndürme şeklinde etki ettiği için, bu etkiler küre üzerindeki iki noktayı sabit bırakırlar. Yani $SO(3)$ grubunun altgrupları $2$-boyutlu küre üzerine serbest bir şekilde etki edemez.

$O(3)$ grubunun altgruplarına bakarsak bu alt-gruplardan bazılarının $2$-boyutlu küre üzerine serbest etkileri olduğunu görüyoruz. Mesela yukarıda gördüğümüz ters kutup etkisi serbest ortogonal bir etkidir. Öte yandan bazı diğer yansıma etkileri nokta sabitleyebiliyor. Mesela $S_4$’ün düzgün dörtyüzlü üzerindeki $(12)$ etkisi bu noktalar arasındaki orta noktayı sabit bırakır. Biraz hesap yaparak $2$-boyutlu küre üzerinde serbest olarak etki eden tek grubun $C_2$ oldugunu ve olası tek etkinin de ters kutup etkisi olduğunu gösterebilirsiniz.

Yüksek boyutlu $S^n$ kürelerinde $C_2$’den başka grupların serbest etkilerini bulmak mümkün.
Bu grupları bulmak için, $SO(3)$ grubu için yaptığımız gibi, önce $SO(n)$ grubunun tüm altgruplarını
bulmak isteyebilirsiniz, ama bu zor bir sınıflandırma problemidir ve sadece bazı küçük boyutlarda
çözümü bilinmektedir. Öte yandan $O(n)$ grubunun bir küreye serbest bir şekilde etki eden tüm altgruplarının sınıflandırılması başarıyla tamamlanmıştır.

Teorem 6.

[Zassenhaus 1935, Suzuki 1955, Wolf 1984] Sonlu bir $G$ grubunun herhangi bir boyuttaki bir küre üzerine ortogonal temsillerden gelen bir serbest etkisi olması için gerek ve yeter koşul aşağıdaki iki özelliği sağlamasıdır:

1. Her $p$ ve $q$ asal sayısı için $G$’nin eleman sayısı $pq$ olan tüm altgrupları, devirli gruplardır.
2. $G$ grubu $p>5$ için $SL_2(\mathbb{F}_p)$ grubunu altgrup olarak içermez.

Burada $SL_2(\mathbb{F}_p)$ grubu, determinantı $1$ olan ve girdileri $\mathbb{F}_p$ cisminin elemanları olan $2\times 2$ matrislerinin grubudur. İlk maddede ifade edilen özelliğe genelde $pq$-koşulu denir. Küreler üzerine serbest ortogonal etkiye sahip grupların bu özelliğe sahip olması gerektiğini göstermek kısmen kolay. Bu özelliğe sahip tüm çözünür grupların küreler üzerine serbest etkileri olduğunu ilk gösteren kişi 1935 yılında Zassenhaus olmuş. $p^2$-koşulunu sağlayan çözünür olmayan sonlu grupların sınıflandırması Suzuki tarafından yapılıyor. Bu sınıflandırma teoreminin tam ispatını ve bu konudaki tüm referansları Wolf’un uzay formları üzerine yazdığı şu kitapta bulabilirsiniz [16].

Topoloji açısından ortogonal temsillerden gelen grup etkileri oldukça özel etkilerdir. Hatırlayacağınız üzere topolojik etkiler sadece süreklilik koşuluyla tanımlanmıştı. Bu etkilerin mesafe korumaları gerekmez. Dolayısıyla topolojik etkiler açısından $pq$-koşulu çok kuvvetli bir koşuldur. Daha önce bahsi geçen birçok grubun $pq$-özelliğini sağlamadığını görebilirsiniz.

Örnek 18.

1. $S_3$ grubu 6 elemanlıdır ve bu devirli bir grup değildir. Dolayısıyla $S_3$ grubu $p=2$ ve $q=3$ için $pq$-koşulunu sağlamaz.
2. $p$ bir asal sayı iken $D_{2p}$ dihedral grubu $2p$-koşulunu sağlamaz.
3. $\mathbb Z/7 \rtimes \mathbb Z/3$ yarıçarpım grubu $p=7$ ve $q=3$ için $pq$-koşulunu sağlamaz.
4. $A_4$ grubunun $\mathbb Z/ 2\times \mathbb Z/2$ grubuyla eşyaplı bir altgrubu vardır, o yüzden $A_4$ grubu $p=2$ için $p^2$-koşulunu sağlamaz.

Bu grupların küreler üzerine ortogonal temsilden gelen etkileri yoktur, ama topolojik serbest etkilerinin olup olmadığı hâlâ sorulabilir.

Topolojik etkiler için ilk kısıtlama P.A. Smith (1938) tarafından bulunuyor. Smith bir küreye serbest etkisi olan sonlu grupların $p^2$-koşulunu sağlaması gerektiğini gösteriyor. Yani bu gruplar $\mathbb Z /p\times \mathbb Z/p$ grubunu altgrup olarak içeremiyorlar. Bunun sonucu olarak yukarıdaki örneklerden $A_4$ grubunun hiçbir şekilde herhangi bir boyutta bir küreye serbest olarak etki edemediğini görüyoruz.

Milnor (1957) küreyle aynı mod-2 homolojisine sahip çokkatlılar üzerine serbest etkisi olan sonlu grupların, $2p$-koşulunu sağlamaları gerektiğini gösteriyor. Yani bu gruplar $D_{2p}$ dihedral grubunu altgrup olarak içeremiyorlar. $S_3$ grubu bu koşulu sağlamayan en küçük grup ve bir küreye hiçbir zaman serbest olarak etki edemiyor.

$p^2$-koşulunu sağlayan grupların, bir küreye homotopik olan sonlu simpleksel komplekslere serbest olarak etki edebildiğini ilk kez Swan (1960) gösteriyor. Swan’ın bu çalışması homoloji cebiri metotlarının ve cebirsel $K$-teorisinin önemli uygulamalarından biri olarak kabul edilir. Swan özel olarak $S_3$ grubunun serbest olarak etki ettiği üç boyutlu küreye homotopik bir simpleksel kompleks inşa ediyor.

$p^2$ be $2p$ koşulunu sağlayan sonlu grupların bir küreye serbest olarak etki ettiği Madsen, Thomas ve Wall (1976) tarafından ameliyat teorisi kullanarak gösteriliyor. Bu teoriyle $C_7 \rtimes C_3$ grubu gibi $pq$-koşulunu sağlamayan sonlu grupların bir küre üzerine serbest olarak etki edebildiğini görüyoruz. Bu etkiler ortogonal temsillerden gelen serbest etkileri olamayacağı için elde edilen bu etkilere egzotik etkiler deniyor. Bu egzotik etkileri gözümüzde canlandırmamız mümkün degil.

Bütün asal sayılar için $p^2$ ve $2p$ koşullarını sağlayan sonlu grupların sınıflandırması, Zassenhaus (1935) ve Suzuki (1955)’nin çözünür olan ve olmayan gruplar için ayrı ayrı yaptıkları çalışmalar sonucunda elde ediliyor. Topolojik etkiler için sınıflandırma probleminin çözümü şu şekilde ifade edilebilir.

Teorem 7.

[Smith 1938, Swan 1960, Milnor 1957, Madsen-Thomas-Wall 1976, Zassenhaus 1935, Suzuki 1955]
Bir küreye serbest olarak etki edebilen sonlu gruplar tam olarak aşağıdaki iki koşulu sağlayan
gruplardır:

1. $G$ grubu $p^2$ koşulunu sağlar ($G$’nin $\mathbb Z/ p\times \mathbb Z/p$ ile eşyapılı bir altgrubu yoktur).
2. $G$ grubu $2p$ koşulunu sağlar ($G$’nin $D_{2p}$ ile eşyapılı bir altgrubu yoktur).

Bu sınıflandırma teoreminin hikayesini ve yukarıda bahsi geçen tüm çalışmaların referanslarını şu makalelerde bulabilirsiniz: [5] ve [8]

Kürelerin üzerine serbest etkileri olan sonlu grupların sınıflandırmasıyla ilgili soruların benzerlerini
başka uzaylar için de sorabiliriz.

Soru 2.

Hangi sonlu gruplar $k$ tane kürenin çarpımına $S^{n_1}\times \cdots \times S^{n_k}$ serbest olarak etki eder?

Bu soru $k=2$ için bile hala yanıtlanamamıştır. Buradaki beklenti, üzerinde serbest $G$-etkisi olan çarpım uzayındaki kürelerin sayısının, $G$ grubun içindeki abelyen altgrupların yapısını kısıtladığı yönündedir.

Bunu daha iyi ifade edebilmek için bir grubun rankı ne demek onu tanımlayalım.

Tanım 14.

$G$ sonlu bir grup, $p$ asal bir sayı olsun. $G$ grubunun $p$-rankı şu şekilde tanımlanıyor:
$$\textrm{rk}_p (G)=\max \{ s \, | \, (\mathbb Z /p)^s \leq G \}$$
$G$ grubunun rankı $p$-ranklarının maximumu olarak tanımlanıyor ve $\textrm{rk}(G)$ ile gösteriliyor.

Örnek 19.

$A_4$ alterne grubu için $\textrm{rk}_2(A_4)=2$, $\textrm{rk}_3(A_4 )=1$, dolayısıyla $\textrm{rk} (A_4)=2$.

Sanı 1. (Klasik rank sanısı)

Eğer sonlu $G$ grubu $k$ tane kürenin çarpımına $$X=S^{n_1}\times \cdots \times S^{n_k}$$
serbest olarak etki ediyorsa $ \textrm{rk} (G)\leq k$ eşitsizliği sağlanır.

Bu sanı eşit boyutlu kürelerin çarpımı için büyük oranda çözülmüştür, ama farklı boyutlardaki kürelerin çarpımı için hâlâ açıktır. Ben doktora tezimde rank sanısının $X=(S^1)^k$ için doğru olduğunu göstermiştim ve bunu yapmam beş yıl sürmüştü. Eşit boyutlu kürelerin çarpımı için $n=3$ ve $7$ iken bu sanının doğru olup olmadığı hâlâ bilinmiyor. Buna bakarak genel durumu çözmenin kolay olmayacağı söylenebilir, ama bir soruyu çözmeye başlamanın ilk aşaması o sorunun zorluğunu ciddiye almamaktan geçer. O yüzden şimdiden soru zordur diye bu problemi çözmeye çalışmaktan korkmayın.

Rank sanısıyla ilgili daha fazla bilgi için [1] makalesine bakabilirsiniz. Bu soruları ileri düzeyde çalışmak için bu konuda Özgün Ünlü ile yazdığımız bazı makaleleri indirip okuyabilirsiniz [17].

Kaynaklar

1. A.~Adem, Lectures on the cohomology of finite groups, Contemporary Mathematics 436 (2007): 317.
2. M.~A.~Armstrong, Groups and Symmetry, Springer, 1997.
3. A.~O.~Asar, A.~Arıkan ve A.~Arıkan, Cebir, Palme Yayıncılık, 2010.
4. V.~Climenhaga ve A.~Katok, From Groups to Geometry and Back, AMS Student Library Vol. 81, 2017.
5. J.~F.~Milgram ve R.~J.~Milgram, A survey of the spherical space form problem, Mathematical Reports,  Vol. 2, Part 2, Harwood Press, 1985.
6. D.~S.~Dummit and R.~M.~Foote, Abstract Algebra, Vol. 1999, Prentice Hall, 1991.
7. Z.~Ercan, Topoloji, ODTÜ yayıncılık, 2021.
8. I.~Hambleton, Topological spherical space forms, Handbook of Group Actions (Vol. II), ALM 32 (2014),  151-172. International Press, Beijing-Boston.
9. J.~Lee, Introduction to Topological Manifolds, Vol. 202, Springer, 2010.
10. J.~R.~Munkres, Topology, Prentice Hall, 2000.
11. D.~Newcomb, Symmetry Groups of Platonic Solids,  https://dnewcomb.com/pdfs/Platonic%20Solids.pdf
12. J.~O’Connor, Topics in Geometry, Lecture Notes,  http://campbell.mcs.stand.ac.uk/$\sim$john/geometry/Lectures/L10.html
13. Y.~Ozan, Türevlenebilir Manifoldlara Giriş, ODTÜ Yayınları, 2016.
14. J.~S.~Rose,  A Course on Group Theory, Courier Corporation, 1994.
15. V.~S.~Varadarajan, Lie groups, Lie algebras, and their representations, Vol. 102, Springer, 2013.
16. J.~Wolf, Spaces of Constant  Curvature (5th edition), Publish or Perish, 1984.
17. E.~Yalçın, http://www.fen.bilkent.edu.tr/$\sim$yalcine.