Yazar: Cem Tezer
Yıl: 1992-5
Sayı: 10
Bu yazıda “çokgen” kelimesiyle, kendi kendini kesmeyen, kapalı (yani kendi başladığı noktada biten) bir kırık çizgi tarafından sınırlandırılmış bir düzlem bölge kastedeceğiz. Bu kavramlara şekillerle açıklık kazandıralım: Şekil 1a, 1b, 1c de sırayla kendini kesen, kendini kesmeyen, kendini kesmeyen ve kapalı birer kırık çizgi görülüyor.
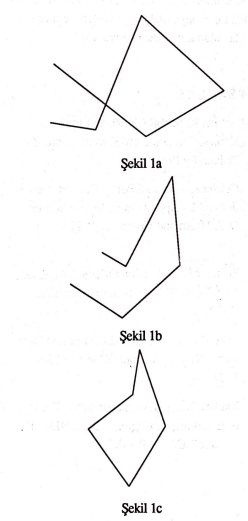
Tabii Şekil 1c deki kırık çizgi istediğimiz özelliklere sahip olup bir çokgen sınırlandırmaktadır. Bazı özel durumlarda, birbirini en fazla sınır noktalarında kesen çokgenlerin birleşimine de çokgen diyeceğiz.
Şimdi yazımızın konusunu teşkil eden eşparçalama kavramına geçebiliriz:
Tanım: $\varphi $ ve $\psi$ gibi iki çokgen ve bir $n \in \mathbb{N}=\{ 1, 2, 3, … \}$ verildiğinde, eğer
a) $ \varphi = \varphi_1 \cup \varphi_2 \cup … \cup \varphi_n$
$ \psi = \psi_1 \cup \psi_2 \cup … \cup \psi_n$
$n^\prime \leq n$ olacak,
b) Her $ i\in \{1, 2, 3, …, n^\prime \}, $ için $\psi_i, \varphi_i$’ye izometrik olacak ([2]),
c) Her $i, j \in \{1, 2, 3, …n^\prime \}, i \neq j$ için $\varphi_i, \varphi_j$ ‘yi ve $\psi_i, \psi_i$ ‘yi ancak sınır çizgisine ait bir noktada kesecek şekilde bir $n^\prime \in \mathbb{N}$ ve $\varphi_1, \varphi_2, …, \varphi_n, \psi_1, \psi_2, …, \psi_n$ çokgenleri varsa, “$\varphi$ çokgeni $\psi$ çokgenine $n$-eşparçalanabilir” diyeceğiz.
Matematiğin bir cilvesi olarak, aslında basit bir fikri böyle çetrefil bir şekilde sunmak zonında kaldık. Ömekleıe geçmeden önce eşpaıçalanmayı daha gündelik bir dille bir daha taif edilim: Aslında “$\varphi$ çokgeni $\psi$ çokgenine $n$- eşparçalanabilir” dediğimizde şunu kastediyoruz: Kağıttan (veya başka bir iki boyutlu malzemeden) $\varphi$ çokgenin bir nüshasını hazırlasak, bunu makasla $n$ veya daha az alt çokgene ayırabiliriz ki, bu altçokgenler tekrar bir araya geürilerek (tabii genel olarak başka bir konumda !) $\psi$ çokgeni elde edilebilir.
Hemen ilk örneğimize geçelim: Şekil 2 de bir $\varphi$ çokgeninin beş altçokgene bölünerek nasıl $\psi$ çokgenine “eşparçalandığı” görülüyor.
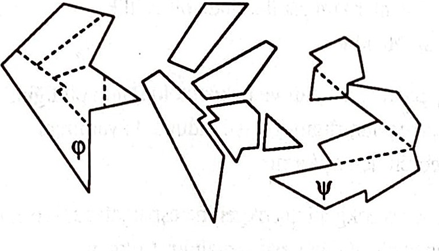
Bir eşkenar üçgen beş altçokgene bölünerek bir kareye (tabii alanca eşit bir kareye) eşparçalanabilir. Okuyucu bunun nasıl yapıldığını Şekil 3 ten çıkarabilir. ([3])
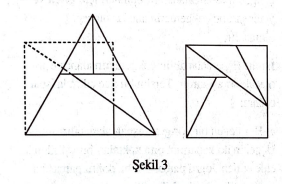
Belki izaha muhtaç olan tek husus, sözkonusu üçgendeki yatay çizginin kenar orta noktalarını birleştirmekte olduğudur.
Bu açıklamalardan sonra okuyucu herhalde yeni bir maceranın heyecanını duymaya başlamıştır. Onu daha da tahrik etmek için şu soruyu soralım: Acaba bir eşkenar üçgen beşten daha az sayıda altçokgen kullanılarak bir kareye eşparçalanabilir mi? Bu soruya yazımızın sonunda tekrar döneceğiz.
Büyük eşparçalama ustası H. Lindgren’den bir de mühr-i-Süleyman – eşkenar üçgen eşparçalaması sunalım: ([5], s. 85)
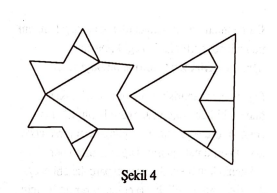
Yazımızın merkezini teşkil edecek olan esas teoreme geçmeden önce eşparçalama konusunun matematikteki yelini biraz belirleyelim. İşin eğlencelik tarafı hakkında uzun uzadıya konuşmaya gerek yok. Bu noktada okuyucuya H. Lindgren’in harikulade kitabını ([5]) ve M. Gardnef’ın zarif makalesini ([4]), önemle tavsiye edelim. Ayrıca V.G. Boltyanskii’nin derli toplu kitabı [1] dilimize kazandırılmış olup kıymetli bir kaynaktır. Bundan başka, eşparçalama ve benzeri kavramlar geometrinin ve genel olarak matematiğin temelleri hakkında bir çok çalışmaya konu olmuş. Bu yönde çalışma yapmış matematikçilerden M. Dehn, F. Hausdorff, S. Banach ve A. Tarski akla ilk gelenlerden
Tarihte eşparçalamanın en eski örneği M.S. 10. yüzyılda yaşamış bir matematikçi olan Ebülvefa’ya ait: Ne yazık günümüze kadar ulaşamamış bir kitabından kalan parçalarda, Ebülvefa’nın bir kareyi dokuz altçokgene ayırıp sonra bu çokgenleri birleştirerek üç çeşit kareye dönüştürüldüğü görülüyor. ([3]) Bu zarif ve az önce söylendiği gibi, bilinen en eski eşparçalamanın anafikri Şekil 5 ten anlaşılabilir.
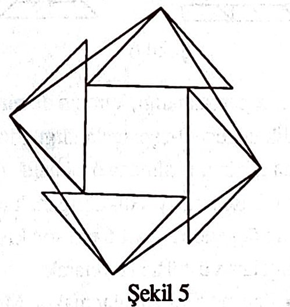
Bir geometri eğitim aracı olarak eşparçalamanın ne kadar değerli olabileceği konusunu öğretmenlerimizin takdirine bırakıyoruz.
Eşparçalama teorisine dönerek, basit fakat önemli birkaç noktaya temas edelim. Eğer $\varphi$ çokgeni $\psi$ çokgenine $n$- eşparçalanabilirse $\psi$ de $\varphi$ ye $n$-eşparçalanabilir. Diğer taraftan her çokgenin kendi kendisine $1$-eşparçalanabileceği de aşikardır. Şimdi, bir $\varphi$ çokgeni bir $n\in \mathbb{N}$ için bir $\psi$ çokgenine $n$-eşparçalanabiliyorsa “$\varphi$ çokgeni $\psi$ çokgenine eşparçalanabilir” diyelim. (Kaç parçada eşparçalandığı mühim değil!). Az evvel söylenenlerin ışığında, eşparçalanabilirliğin düzlemdeki çokgenler kümesi üzerinde yansımalı ve bakışık bir bağıntı olduğu görülüyor. Böylece önemli ve teknik bir önermeye sıra geliyor.
Yardımcı Teorem : Eğer $\varphi$ çokgeni $\psi$ çokgenine $m$-eşparçalanabilir, $\psi$ çokgeni $\xi$ çokgenine $n$-eşparçalanabilirse, $\varphi$ çokgeni de $\xi$ çokgenine $mn$-eşparçalanabilir.
Bu yardımcı teoremin ispatı, yazının girişindeki tarif nevinden aslında çok basit bir fikri teknik bir kıyafete sokmaktan ibaret. Anafikri bir örnekle Şekil 6 yardımıyla açıklamakla yetineceğiz: Şekil 6 da ince uzun bir dikdörtgenin
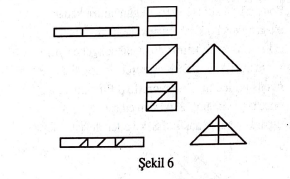
bir kareye $3$-eşparçalandığı, karenin de bir ikizkenar dik üçgene $2$-eşparçalandığı görülüyor. Yani burda gözönüne alınana özel halde $m=3, n=2, \varphi, \psi, $ ve $\xi$ ise sırasıyla dikdörtgen, kare ve ikizkenar dik üçgendir. Şekil 6 nın son kısmında bu iki eşparçalama üst üste koyularak dikdörtgen, üçgene 6-eşparçalanmakta. Meraklı okuyucu bu örnekten yola çıkarak tam bir ispat yazabilir.
Teorem 1: Eşparçalanabilirlik düzlem çokgenler kümesi üzerinde bir eşitlik bağıntısıdır.
İspat: Yansımalı ve bakışık olduğunu bildiğimiz eşparçalanirlığın, geçişli olduğu da yardımcı teoremden aşikardır.
Eğer $\varphi$ çokgeni $\psi$ çokgenine eşparçalanabilirse, $\varphi$ ve $\psi$ nin alanları eşit olmalıdır. Çokgen eşparçalanabilirlik konusunun temel sonucu olan Gerwin-Bolyai teoremi bu gerek şanın aynı zamanda da yeter olduğunu işaret etmektedir.
Teorem 2: (Gerwin – Bolyai Teoremi): iki çokgenin eşparçalanabilir olmaları için gerek ve yeter şart bu çokgenlerin alanlarının eşit olmasıdır.
İspat: Eşparçalanabilir çokgenlerin alanca eşit olacakları aşikardır. Tersini bir kaç adımda ispat edelim:
a) Her üçgen bir dörtgene eşparçalanabilir: Üçgenin iki kenarının orta noktalan birleştirilerek elde edilen doğru parçası ve bu doğru parçasına üçüncü köşeden indirilen dikme üçgeni üç altüçgene ayırır. Bu üçgenler hareket ettirilerek kolayca bir dikdörtgen elde edilir. (Şekil 7)
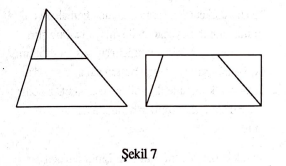
b) Her dikdörtgen bir kareye eşparçalanabilir: Bu eşparçalanabilirliği Şekil 8 de özetlemeyi yeterli görüyoruz. Sözkonusu dikdörtgen ne kadar uzun olursa o kadar çok parçaya gerek duyulacağını hatırlatalım.
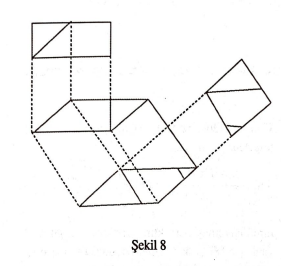
c) Alanca eşit iki üçgen eşparçalanabilir. Bu artık a) ve b) den dolayı aşikardır, alanlanrı aynı olan üçgenler aynı karelere eşparçalanabilir.
d) Herhangi bir çokgen bir üçgene eşparçalanabilir: Aslında bu ispatın çokgenin kenar sayısı üzerinde tümevarımla yapılması gerekir. Biz dışbükey bir dörtgenin bir üçgene eşparçalandığını göstermekle yetineceğiz. Bunu genel dörtgenler için yapmayı okuyucuya bırakıyoruz. Bu basit fikri okuyucu beşgenleri dörtgenlere, altıgenleri beşgenlere v.b. eşparçalamakta kullanabilir. ABCD dışbükey bir dörtgen olsun (şekil 9)
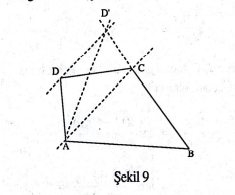
$D$’den $AC$’ye çizilen paralel $BC$’yi $D$’de kessin. $ADC$ ve $AD’C$ üçgenleri alanca eşit olup eşparçalanabilirler. Demek ki $ABCD$ dörtgeni de $AD’C$ üçgenine eşparçalanır.
e) Alanca eşit $\varphi$ ve $\psi$ çokgenlerini ele alalım. $\varphi$ ve $\psi$ sırasıyla alanca kendilerine eşit $\hat{\varphi}$ ve $\hat{\psi}$ üçgenlerine eşparçalanabilerler. $\hat{\varphi}$, $\hat{\psi}$ alanca eşit üçgenler olup birbirlerine eşparçalanabilirler Demek ki $\varphi$,$\psi$ birbirlerine eşparçalanabilirler.
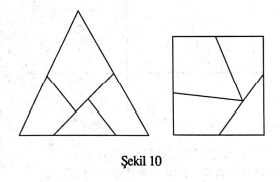
Gerwin-Bolyai teoremi gerçekten de alanları eşit iki verilmiş çokgeni eşparçalamakta doğrudan kullanılabilir. Fakat genel olarak, bu teoremi takip ederek elde edilen eşparçalmalarda çok sayıda, bu yüzden de çok ufak altçokgenler ortaya çıkar. Bu bizi “Alanca eşit iki çokgen en az kaç alt çokgen kullanılarak eşparçalanabilir?” sorusuna götürüyor. Bu, hakkında mütehassısların “sokaktaki adam” dan daha fazla birşey bilmediği çok zor bir konudur. Durumu en iyi kare-eşkenar üçgen problemi ile örnekleyebiliriz: Yazımızın başında bu çokgenlerin beş altçokgen kullanılarak eşparçalanabildiğine dikkat çekmiştik. Aynı işin dört altçokgenle yapılabileceği 1902 de H.E. Dudeney tarafından gösterilmiştir. ([5]). Şekil 10 da Dudeney’in harikulade eşparçalanmasını sunarak yazımızı bitirelim.
KAYNAKLAR:
1) V. G. Boltyanskii: “Eşdeğer ve Eşparçalanabilir Şekiller”, Altınbaş Büke tarafından Türkçe’ye çevrilmiş. Türk Matematik Derneği Yayınları, İstanbul1964.
2) H. Demir “İzometriler”, Matematik Dünyası, Cilt 1, Sayı 2, 1991
3) H. Eves “A Survey of Geometry” Allyn and Bacon, Boston 1968
4) M. Gardner “Matematical Games” Scientific American, 205 158-169 1961.
5)H. Lindgren “Receational. Problems in Geometric Dissections and How to Slve Them” Dover Publications, Inc., New York 1972.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

