Yazar: C. Alparslan Ertuğ
Yıl: 1994-4
[1]’den özetleyerek çevirdiğimiz yazının ilk bölümü dergimizin Nisan 1994 sayısında yayınlandı. Bu bölümde ise, sözü geçen yazıda belirtilen çözüm yöntemlerinin dörtgen ve çember problemlerine ilişkin uygulamalarını örneklerle göstermek istiyoruz.
Örnek 1. Bir $A B C$ üçgeninin $m_a$, $m_b$, $m_c$ kenarortayları bilindiğine göre, $AC=b$ kenarını bulunuz.
Çözüm. Kenarortayların kesişme noktasına $M$ diyelim. Bu nokta kenarortayı 2/3 oranında böler (Şekil 11). Bu nedenle $AMC$ üçgeninin iki kenarı ve bir kenarortayı bulunmuş olur.
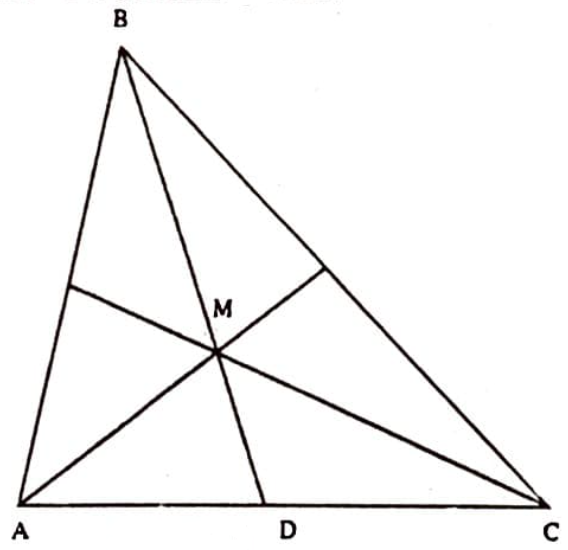
$\overline{A M}=\frac{2}{3} m_{a}$, $\overline{M C}=\frac{2}{3} m_{c}$, $\overline{M D}=\frac{1}{3} m_{b}$. $A M C$ üçgenini göz önüne alalım. Kenarortayı kendisi kadar uzatıp $A M C P$ paralelkenarını elde edelim (Şekil 12).
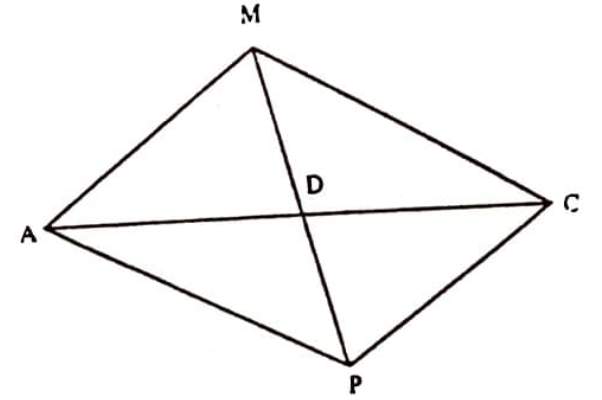
$A M C P$ için metrik bağıntıyı yazalım: $$
\begin{split}
\overline{A C}^{2}+\overline{M P}^{2} &=2 \overline{A M}^{2}+2 \overline{M C}^{2} \\
b^{2}+\frac{4}{9} m_{b}^{2} &=2 \frac{4}{9} m_{a}^{2}+2 \frac{4}{9} m_{v}^{2}
\end{split} $$ Buradan da $b=\frac{2}{3} \sqrt{2 m_{a}^{2}+2 m_{c}^{2}-m_{b}^{2}}$ elde edilir.
Örnek 2. Bir $A B C$ üçgeninin $A B$ ve $B C$ kenarları üzerine $A B D E$ ve $B C K M$ kareleri çiziliyor. $D M$ doğru parçasının, üçgenin $B P$ kenarortayının uzunluğunun iki katı olduğunu kanıtlayınız (Şekil 13).
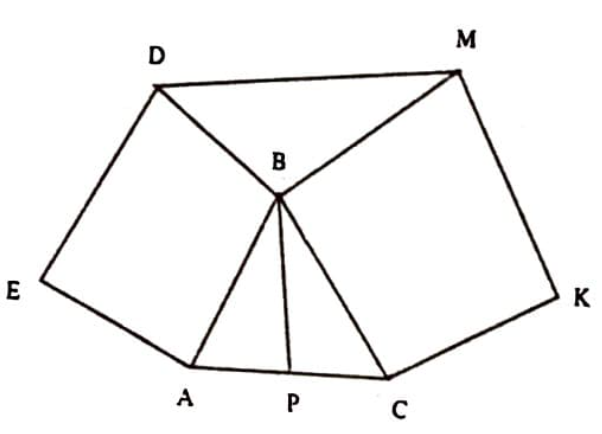
Çözüm. $\overline{D M}=2 \overline{B P}$ olduğunu göstereceğimize göre, $B P$ kenarortayını kendisi kadar uzatıp $A B C$ üçgenini $A B C T$ paralelkenarına dönüştürmemiz ve sonra da $\overline{D M}=\overline{B T}$ olduğunu ispatlamamız yeterli olacaktır (Şekil 14).
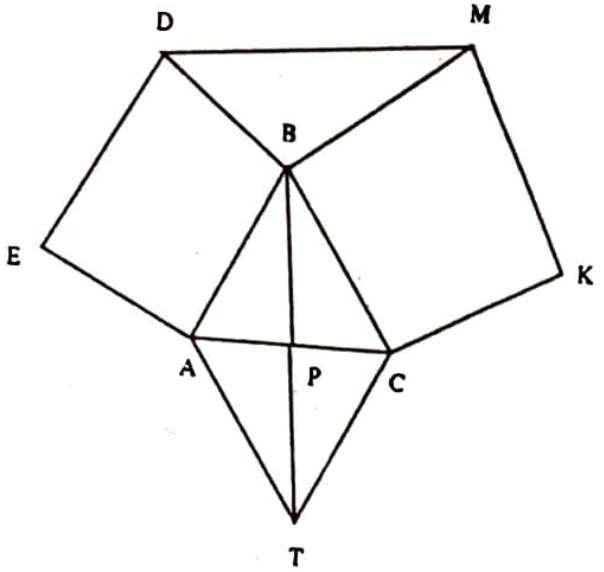
$D M$ ve $B T$ doğru parçalarının eşitliğini kanıtlamak için, bu doğru parçalarının kenarlarını iki üçgenin kenarları olarak almak ve bu üçgenlerin eş oldukların göstermemiz gerekecektir. Şimdi verilen problemi bu yönteme uygun olarak çözelim.
$D M B$ ve $B C T$ üçgenlerini gözönüne alalım: $\overline{B M}=\overline{B C}$ ($B M K C$ karesinin kenarları), $\overline{D B}=\overline{A B}$ ($B D E A$ karesinin kenarları) ve $\overline{A B}=\overline{C T}$ ($A B C T$ paralelkenarının karşılıklı kenarları). O halde $\overline{D B}=\overline{C T}$ olur. $\sphericalangle D B M=$ $\sphericalangle B C T$ (kenarları birbirine dik açılar). Buna göre, $D M B$ ve $B C T$ üçgenleri kenar-açı-kenar bağıntısından eşittirler. Buradan da $\overline{D M}=\overline{B T}$ bulunur ve $\overline{B T}=2 \overline{B P}$ sonucu elde edilir.
Örnek 3. $x$ noktası $A B C D$ dörtgeninin $A D$ kenarının ortasıdır (Şekil 15). $A D: A B=\sqrt{2}$ olduğu bilindiğine göre, $B K$ ile $A C$ köşegeni arasındaki açıyı bulunuz.
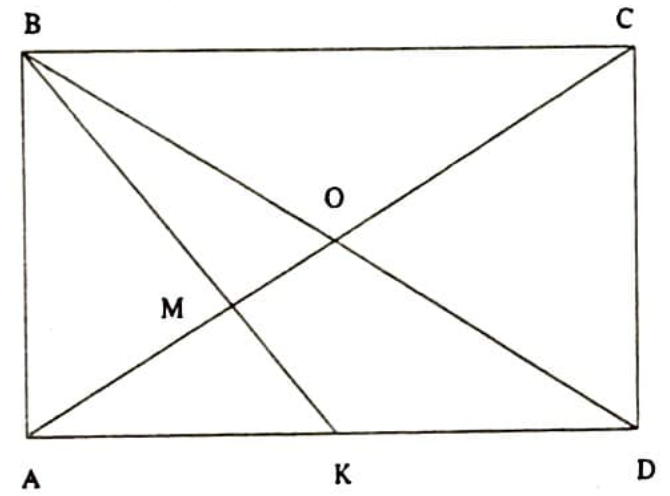
Çözüm. Yardımcı parametre yöntemini uygulayalım. $\overline{A B}=a$ dersek, $\overline{A D}=a \sqrt{2}$ olur. Çözüm yolumuz şöyle olacaktır: Önce $A M K$ üçgeninin kenarlarını $a$ cinsinden ifade eder, sonra da $A K$ kenarına göre kosinüs teoremini uygularız. Bu, $x$ ile gösterdiğimiz ve bulmaya çalıştığımız $A M K$ açısının kosinüsünü hesaplamamızı sağlar. $A O$ ve $B K$ doğru parçaları $A B D$ üçgeninin kenarortaylarıdır. O halde $\overline{M K}=$ $\frac{1}{3} \overline{B K}$ ve $\overline{A M}=\frac{2}{3} \overline{A O}$ olacaktır. $$ \begin{split} M K &=\frac{1}{3} \overline{B K}=\frac{1}{3} \sqrt{\overline{A B}^{2}+\overline{A K}^{2}} \\
&=\frac{1}{3} \sqrt{a^{2}+\left(\frac{a \sqrt{2}}{2}\right)^{2}}=\frac{a \sqrt{6}}{6} \\
\overline{A M} &=\frac{2}{3} \overline{A O}=\frac{1}{3} \overline{A C} \\
&=\frac{1}{3} \sqrt{\overline{A D}^{2}+\overline{C D}^{2}}\\
&=\frac{1}{3} \sqrt{(a \sqrt{2})^{2}+a^{2}}=\frac{a \sqrt{3}}{3} \end{split} $$
$A M K$ üçgeninde ise, $\overline{A K}=\frac{a \sqrt{2}}{2}$, $\overline{A M}=\frac{a \sqrt{3}}{3}$, $\overline{M K}=\frac{a \sqrt{6}}{6}$ değerlerini kullanarak kosinüs teoremini uygularsak aşağıdaki eşitliği elde ederiz: $$ \begin{split} \overline{A K}^2 &= \overline{A M}^2+\overline{M K}^2-2\overline{A M}\,\overline{M K}\cos x\\
\left(\frac{a \sqrt{2}}{2}\right)^{2} &=\left(\frac{a \sqrt{3}}{3}\right)^{2}+\left(\frac{a \sqrt{6}}{6}\right)^{2} -2 \frac{a \sqrt{3}}{3} \frac{a \sqrt{6}}{6} \cos x \\
& \frac{a^{2}}{2}=a^{2}+\frac{a^{2}}{6}-\frac{a^{2} \sqrt{2}}{3} \cos x \end{split} $$ Buradan da $\cos x=0$ ve dolayısıyla da $x=90^{\circ}$ bulunur.
Örnek 4. $a$ ve $b$ bir dik üçgenin dik kenarları, $c$ hipotenüsü ve $r$ ise içteğet çemberinin yarıçapı olduğuna göre, $r=\frac{a+b-c}{2}$ olduğunu gösteriniz.
Çözüm. İçteğet çemberinin $O$ merkezinden ve değme noktalarından $O D$, $O E$ ve $O F$ yarıçaplarını çizelim. $O D \perp B C$, $O E \perp A C$ ve $O F \perp A B$ olacaktır (Şekil 16).
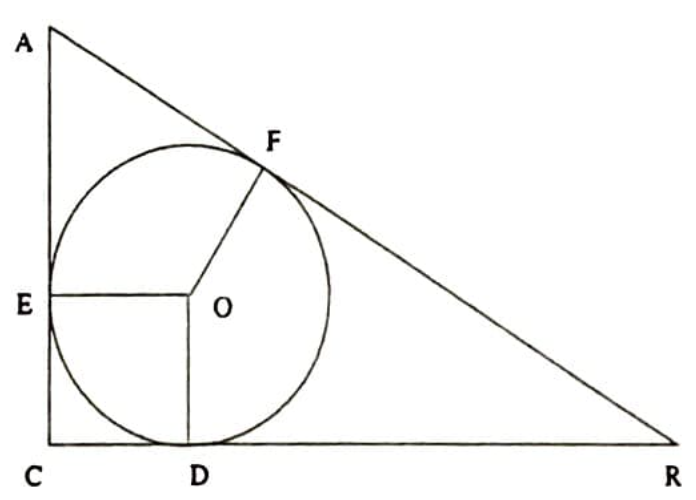
$O D C E$ bir kare olacağı için (bütün açıları dik ve $\overline{O E}=\overline{O D}$), şu eşitlikleri yazabiliriz: $\overline{C E}=\overline{C D}=r$, $\overline{B D}=a-r$, $\overline{A E}=b-r$, $\overline{B D}=\overline{B F}$, $\overline{A E}=\overline{A F}$, $\overline{B F}=a-r$ ve $\overline{A F}=b-r$. Öte yandan $\overline{A B}=\overline{B F}+\overline{A F}$ olduğu şekilden görülmektedir. Yukarıda bulunan değerleri bu eşitlikte yerine koyarsak sonuca ulaşırız: $c=(a-r)+(b-r)$ ve $r=\frac{a+b-c}{2}$.
Uyarı. Bu elde ettiğimiz formül, dik üçgenlere ait problemlerin çözümünde sık sık kullanılır.
Örnek 5. $R$ yarıçaplı bir çember, bir karenin birbirine komşu iki köşesinden geçiyor. Karenin üçüncü köşesinden çembere çizilen teğetin uzunluğu karenin kenarının iki katıdır. Karenin kenar uzunluğunu bulunuz.
Çözüm. $\overline{A B}=x$ ve $\overline{B M}=2 x$ diyelim (Şekil 17).
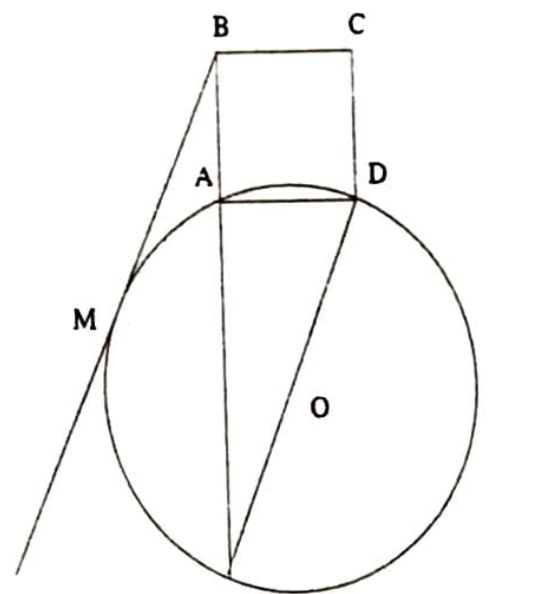
$A B$ kenarını uzatalım ve bu uzantının çemberi kestiği nokta $K$ olsun. $\overline{B K}\cdot \overline{A B}=\overline{B M}^{2}$, $\overline{B K} x=4 x^{2}$. Buradan da $\overline{B K}=4 x$ ve $\overline{A K}=3 x$ olarak bulunur. $\widehat{K A D}=90^{\circ}$ olması nedeniyle $K D$ çemberin çapıdır. $A D K$ dik üçgeninden $\overline{A D}^{2}+\overline{A K}^{2}=\overline{K D}^{2}$, $x^{2}+9 x^{2}=4 R^{2}$ yazılır ve buradan da $x=\frac{R \sqrt{10}}{5}$ bulunur.
Örnek 6. Bir çeyrek daire dilimi verilmiş olsun. Merkezi, yayın bitim noktasında olan ve yarıçapı aynı olan ikinci bir çember çiziliyor, ve bu çember daire dilimini iki parçaya ayırıyor. Bu iki parçadan küçük olanın içine bir çember çiziliyor. Bu çemberin yarıçapının, daire diliminin yarıçapına oranını bulunuz.
Çözüm. $O_{1} O_{2}=R$ diyelim ve içeri çizilen çemberin yarıçapı $r$’yi $R$ cinsinden ifade etmeye çalışalım (Şekil 18).
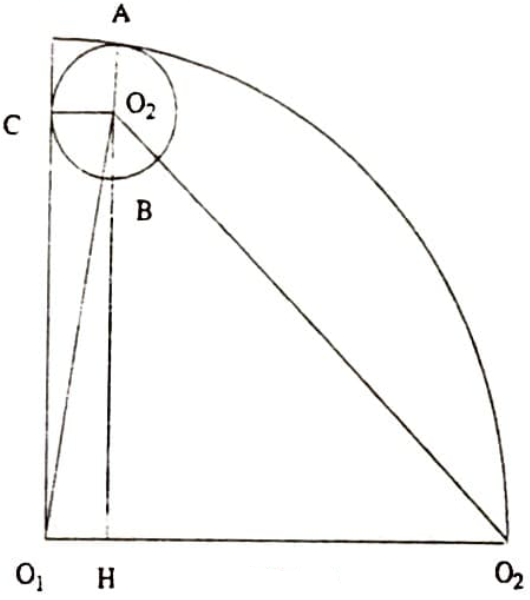
Şimdi $O_{1} O_{2}O_{3}$ üçgenini gözönüne alalım. $O_{1} O_{2}=R$, $O_{1} O_{3}=R-r$ ve $O_{2} O_{3}=R+r$ olduğu görülmektedir. $O_{3} H$ yüksekliğini çizelim. $O_{1} H=O_{3} C=r$ ve $O_{2} H=R-r$ olacaktır. $O_{3} H$’yi bir referans elemanı olarak alalım. $O_{1} O_{3}H$ üçgeninden şunları elde ederiz: ${\overline{O_{3} H}}^{2}={\overline{O_{1} O_{3}}}^{2}-\overline{O_{1} H}^{2}=(R-r)^{2}-r^{2}$. ${\overline{O_{3} H}}^{2}$ değerlerini birbirine eşitleyerek şu sonuca ulaşırız: $(R-r)^{2}-r^{2}=(R+r)^{2}-(R-r)^{2}$. Buradan da $r=\frac{R}{6}$ ve dolayısıyla $\frac{r}{R}=\frac{1}{6}$ buluruz.
Örnek 7. Yarıçapları $r$ ve $R$ olan iki çember dıştan teğettirler; $A B$ ve $C D$ ise dış teğetleridir. $A B C D$ dörtgeninin içine bir çember çizilebileceğini gösteriniz ve bu çemberin yarıçapını bulunuz (Şekil 19).
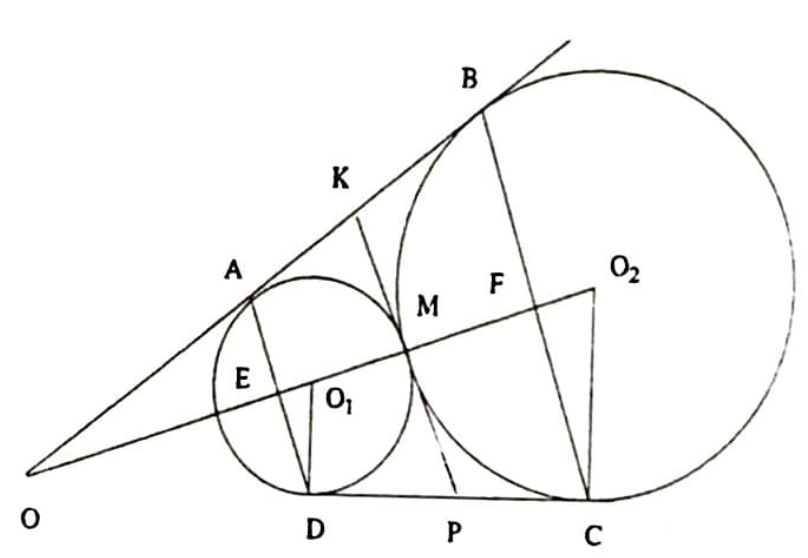
Çözüm. Teğetlerin kesişme noktası olan $O$ ‘yu $O_{1}$ ve $O_{2}$ ile birleştirelim ve çemberlerin değme noktasındaki ortak teğetlerini çizelim. Ayrıca $O_{1}D$ ve $O_{2} C$ yarıçaplarını da çizelim: $O_{1} D \perp$ $C D$ ve $O_{2} C \perp CD$.
$OO_{2}$ doğrusunun şeklin simetri ekseni olması nedeniyle $A$ ve $D$ noktaları ile $B$ ve $C$ noktaları $OO_{2}$ ‘ye göre simetriktirler. Bu ise $ABCD$ dörtgeninin ikizkenar bir yamuk olduğu anlamına gelmektedir.
$A B C D$ yamuğunun içine bir çember çizilebilmesi için, $\overline{A D}+\overline{B C}=\overline{A B}+\overline{C D}$ eşitliğinin sağlanmasının gerekli ve yeterli olduğu bilinmektedir. Bir teğetler dörtgenini gözönüne alarak ve çemberin dışındaki bir noktadan çizilen teğetlerin eşit olması özelliğinden yararlanarak bunu kolayca kanıtlayabilirsiniz.
$\overline{A B}=\overline{C D}$ olması nedeniyle $\overline{A B}=\frac{\overline{A D}+\overline{B C}}{2}$ eşitliği sağlanmalıdır. Dolayısıyla da $\overline{A B}$’nin $A B C D$ yamuğunun orta tabanına eşit olduğunu kanıtlamak yeterli olacaktır.
Şekilden kolayca görüleceği gibi, $\overline{A K}=\overline{K M}$, $\overline{B K}=\overline{K M}$, $\overline{D P}=\overline{P M}$ ve $\overline{C P}=\overline{P M}$’dir. Dolayısıyla $\overline{A K}+\overline{B K}+\overline{D P}+\overline{C P}=$ $\overline{K M}+\overline{K M}+\overline{P M}+\overline{P M}$’dir. $\overline{A B}+\overline{D C}=2 \overline{K P}$ bulunur. $\overline{A B}=\overline{D C}$ olduğu gözönüne alınacak olursa, $\overline{A B}=\overline{K P}$ bulunur.
Böylece söz konusu yamuğunun içine bir çember çizilebileceğini göstermiş olduk. $E F$ bu çemberin çapıdır. $\overline{O_{1} E}=x$, $\overline{O_{2} F}=y$ diyelim. $\overline{M F}=\overline{M E}$ eşitliğinden yararlanarak $$ R-y=r+x \tag{1}$$ buluruz. $O_{1} D E$ ve $O_{2} C F$ üçgenlerinin benzerliğinden $\frac{O_{1} E}{O_{2} F}=\frac{O_{1} D}{O_{2} C}$, yani, $$\frac{x}{y}=\frac{r}{R} \tag{2}$$ yazabiliriz. $(1)$ ve $(2)$ numaralı denklemlerin oluşturduğu sistemi çözerek, $y=\frac{R^{2}-r R}{R+r}$ buluruz. O halde iç teğet çemberin yarıçapı $R-y=\frac{2 R r}{R+r}$ olarak elde edilir.
Kaynakça
[1] V. Gusev, V. Litvinenko & A. Mordkovich, Solving Problems in Geometry, Mir, Moskova.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı ?. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

