Yazar: Burak Karabey (burakkarabey@gmail.com)
Sayı: 111, 2022-1
Sayıların sayı doğrusundaki yerini bulma çalışmaları, öğrenciler açısından birçok matematiksel bilgi ve beceriyi birlikte kullanmak için iyi bir fırsattır. İlkokuldan itibaren görsel bir temsil olarak kabul edilen sayı doğrusu, gerçek sayı kavramının oluşmasına kadar matematik öğrenme ve öğretmede önemli bir yer tutmaktadır. Lise yıllarına kadar sırasıyla doğal sayıların, tamsayıların, rasyonel sayıların ve gerçek sayıların öğrenciler tarafından anlamlandırılmasına yönelik kazanımlara matematik öğretim programlarında rastlamaktayız. Bu kazanım sıralaması içinde rasyonel sayıları anlamlandırmanın, gerçek sayı kavramının gelişimi için en önemli geçiş aşamalarından biri olduğu söyleyebiliriz.
Rasgele seçtiğiniz bir sayıyı sayı doğrusuna gelişigüzel yerleştirdiğimizde bile aslında sayılar hakkında birçok özelliği dikkate almak zorunda kalırız. Diğer sayıların konumlarını düşünür, sayıları birbirleriyle karşılaştırır, sıralar, sayıların aralıkları hakkında bir fikir yürütür ve hatta bazen eşit olması gereken aralıkların eşit görünmemesinden rahatsızlık hissedip yeniden çizeriz. Analizde fonksiyonları incelerken, özellikle grafiklerin çizilmesi sırasında aralıkların boyutu eğriyi anlamamız açısından çok önemlidir. Benzer şekilde bir geometri problemi çözerken yapacağımız bazı önemli yorumlamalarda yanılgıya düşmeyelim diye olabildiğince uzunlukları ve sayıları doğru yerleştirmeye özen gösteririz.
Sayıların sayı doğrusunda en iyi şekilde temsil edilmesiyle ilgili bu hassasiyetimiz, doğal olarak, “Sayıları sayı doğrusunda tam olarak doğru konumlarına yerleştirdiğimizden nasıl emin olabiliriz?” sorusunu akla getirmektedir. Çevremizdeki birçok insana sayı doğrusuna sayıları nasıl yerleştirdiğini sorduğumuzda bunu gayet doğal ve basit bir eylemmiş gibi bize açıklarlar. Ancak birkaç farklı soruyla onları kolaylıkla şaşırtabiliriz. Örneğin, “$\frac{1}{3}$ sayısı sayı doğrusunda nerede?” diye sorduğunuzda, gelebilecek yanıtların birçoğu “0 ile 1 arasında”, “0 ile 1 arasını üç eş parçaya bölersek ilk parça”, “0 ile 1 arasında 0’a yakın” şeklinde olacaktır. Asıl derinlemesine merakı tetikleyen soru “$\frac{1}{3}$ tam olarak nerededir? Bir aralığı üç eş parçaya böldük diye o aralık gerçekten üç eş parçaya bölünmüş olur mu?” diye sorduğumuz zaman ortaya çıkmaktadır.
Bu yazıda rasyonel sayıların sayı doğrusuna nasıl yerleştirilebileceğini, rasyonel sayılarla gerçekleştirilen bazı işlemlerden ve özelliklerinden yararlanarak sayı doğrusu üzerinde bir konum belirleme yöntemiyle göstereceğiz. Bu yöntemle ortaokul düzeyinde rasyonel sayılarla ilgili geometrik inşa yöntemleri kullanılarak öğrencilerin rasyonel sayıların özelliklerini çizimle deneyimlemesini sağlayabilir ve işlemlere ait özellikleri keşfetmelerine imkân tanımış olabiliriz. Lise ve üstü düzey öğrenciler içinse geometrik inşa, denklik bağıntısı ve rasyonel sayıları ilişkilendirerek ilgili öğrencilere daha derinlemesine bir inceleme, belki de yeni fikirler bulma ve bağlantılar kurma fırsatı oluşturabiliriz. İlk olarak kartezyen çarpım, bağıntı ve denklik bağıntısını bir örnekle hatırlamak faydalı olabilir. (Daha detaylı bilgiler için Matematik Dünyası dergisinin 2003-1 Fonksiyon özel sayısı incelenebilir.)
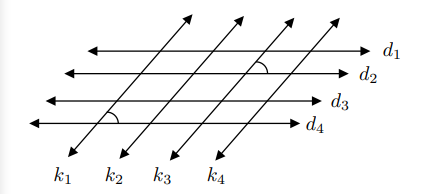
Denklik bağıntısını hatırlamak için doğruların birbirine düzlemde paralel olması durumunu inceleyelim. Bir düzlemdeki tüm doğruların kümesini $E$ olarak adlandıralım. $E \times E$ kartezyen çarpım kümesinin elemanları $(d,k)$ şeklinde doğru çiftleri olacaktır. Bu doğru çiftlerinden paralel olanların kümesini $//$ ile gösterelim ve $E \times E$ kartezyen çarpım kümesinin bir alt kümesi olduğundan bir bağıntı olduğunu hatırlatmadan geçmeyelim.
$$// = \{(d,k): E\text{ düzleminde yer alan }d\text{ ve }k \text{ doğruları paraleldir.}\}$$
Şimdi bu bağıntının özelliklerini inceleyelim.
- Düzlemdeki her $d$ doğrusu kendisine de paralel olduğundan $(d,d) \in //$ olup bağıntımız yansıyandır.
- Bağıntının tanımı gereği düzlemde birbirine paralel tüm $d$ ve $k$ doğruları $//$ bağıntısının bir elemanıdır. $d$, $k$’ye paralelken $k$ de $d$’ye paralel olacağından $(k,d)\in//$ olur ve simetri özelliği sağlanır.
- Son olarak, her $(d,k)$,$(k,l)\in//$ yani bir $d$ doğrusu $k$’ye paralel, $k$ doğrusu da $l$’ye paralelse $d$ doğrusu da $l$’ye paraleldir ve geçişme özelliği sağlanır.
Sonuç olarak $//$ bağıntımız bir denklik bağıntısıdır.
Sayıların sayı doğrusundaki konumunu belirlerken “Neden denklik bağıntısına ihtiyacımız olsun?” sorusuna önemli bir avantaja vurgu yaparak yanıt verebiliriz: Denklik bağıntısı, bir problemi çözerken birbirine denk elemanlardan herhangi birini temsilci olarak kullanabilme ve çözümü denklikteki tüm elemanlara genelleme imkânı sunar. Biz de sayılardan birini doğru bir biçimde konumuna yerleştirirsek ona denk olan sayıları da yerleştirmiş oluruz diyebiliriz.
Paralellik bağıntısına benzer bir denklik bağıntısını rasyonel sayılar üzerinde düşünmek de mümkün. Nasıl mı? Rasyonel sayılar kümesi tamsayı ikililerinden oluşur ve
$$\mathbb{Q}=\{(x,y): \frac{x}{y} \text{ ve }x,y \in \mathbb{Z},y\neq 0\}$$
olarak tanımlanır. $\mathbb{Q}$’da birbirine denk rasyonel sayılar $(q_1,q_2)$ sıralı ikilisi ile gösterilirse;
$$\sim=\{(q_1,q_2 ): q_1=(a,b), q_2=(c,d) \in Q \text{ için }$$
$$(k\cdot a,k\cdot b)=(c,d) ,k \in Z-{0}\text{ yani }\frac{(k\cdot a)}{(k\cdot b)}=\frac{c}{d}\}$$
ile tanımlanan bağıntı da yansıma, simetri ve geçişkenlik özelliklerini sağladığından bir denklik bağıntısıdır. Burada $q_1$ ve $q_2$’yi denk rasyonel sayılar olarak adlandırılabilir ve $q_1\sim q_2$ ile gösterebiliriz. Böylelikle örneğin;
$$\frac{1}{3}=\{\frac{1}{3},\frac{2}{6},\frac{3}{9},\dots\}$$
denklikle elde edilen denklik sınıfından söz edebilir ve denklik sınıfı içerisindeki herhangi bir eleman yerine $\frac{1}{3}$’ü veya bu küme içerisindeki herhangi bir elemanı kullanabiliriz.
Buraya kadar düzlemde paralel olmanın ve rasyonel sayıların denkliğinin, birer denklik bağıntısı olduğunu gösterdik. Bu iki denklik bağıntısı arasındaki bir ilişki bizi yeni sonuçlara götürebilir mi?
Problem kısmına geçmeden önce tamsayıları sayı doğrusuna yerleştirdiğimizi kabul ettiğimizi belirterek aşağıdaki problemleri yanıtlamaya çalışalım.
Problem 1: $\frac{1}{3}$ sayı doğrusunda tam olarak nerededir?
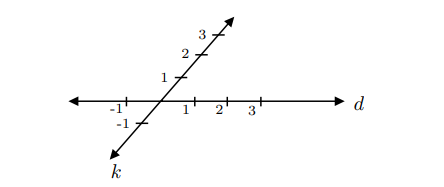
Bir sayı doğrusunda tamsayıları Şekil-2’de olduğu gibi $d$ doğrusuna yerleştirelim ve benzer şekilde $0$’dan geçen başka bir sayı doğrusunu $k$ olarak adlandıralım. Burada amacımız $d$ sayı doğrusuna rasyonel sayıları yerleştirebilmektir.
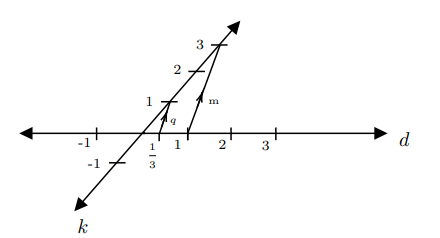
Şekil-3’te $d$ doğrusunda yerini belirlemek istediğimiz rasyonel sayı $\frac{+1}{+3}$, bu durumda +1 sayısını $d$ doğrusunda, +3 sayısını $k$ doğrusunda alarak bir $m$ doğru parçası oluşturalım. Bir doğru parçasına dışındaki bir noktadan bir tek paralel çizilebileceğinden, $m$ doğru parçasına $k$ doğrusu üzerindeki $+1$ noktasından (referans noktası olarak adlandıracağız) bir paralel çizip $q$ doğru parçası olarak adlandıralım. $q$’nun $d$ doğrusunu kestiği nokta üçgende benzerlik gereği $\frac{+1}{+3}$ yani $+\frac{1}{3}$ olacaktır.
Siz de farklı rasyonel sayıları bu yöntemle sayı doğrusuna yerleştirip yerleştiremeyeceğinizi kontrol edebilirsiniz.
Bu yöntem nasıl çalışıyor? Temel olarak üçgende benzerliği (belki bir öncesi Thales teoremini) tamsayılar üzerinden Şekil-4’te olduğu gibi kurguladığımızda $x$ uzunluğu tanım gereği bir rasyonel sayı olacaktır.
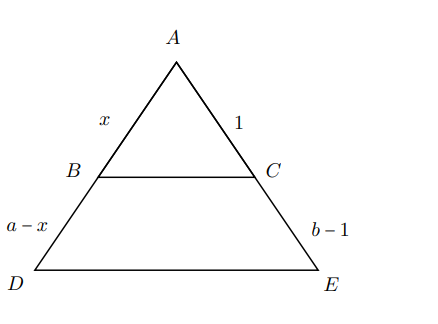
$$\overset{\triangle}{ABC} \sim \overset{\triangle}{ADE}$$
$$\frac{|AB|}{|AD|} = \frac{|AC|}{|AE|}$$
$$\frac{x}{a}=\frac{1}{b} \Rightarrow x=\frac{a}{b}$$
Bu üçgende benzerlik durumunu iki sayı doğrusunun kesişimi üzerinde, Problem 1’de olduğu gibi kurduğumuzda $k$ doğrusu üzerindeki $+1$ noktasından, (üçgenimizde $AB$ uzunluğu) yani referans noktasından çizilen paralel doğrular bize rasyonel sayının $d$ doğrusu üzerindeki konumunu verecektir. Daha kapsamlı bir inceleme için Karabey (2019) makalesine bakabilirsiniz.
Problem 2: $\frac{-1}{+3}$ ve $\frac{+1}{-3}$ rasyonel sayıları birbirine denk midir?
Ortaokuldan itibaren merak edilen sorulardan biri de bir negatif ve bir pozitif tamsayının çarpımının ya da bölümünün neden negatif olduğudur. Bunu açıklamak için farklı yöntemler söz konusu olsa da paralel doğruların denkliği üzerinden bu durumu açıklama şansımız var.
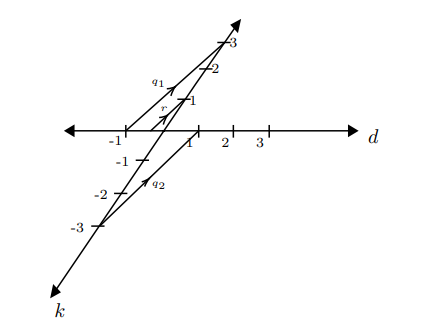
$\frac{-1}{+3}$ ve $\frac{+1}{-3}$ birbirine denkse $d$ doğrusu üzerinde aynı noktaya paralellik ile karşılık gelen sayılar olmalıdırlar, başka bir deyişle aynı denklik sınıfında olmaları gerekir. Bu anlamda Şekil-5’te olduğu gibi ilk olarak $\frac{-1}{+3}$ sayısını, $d$ doğrusundan $-1$’i, $k$ doğrusundan $+3$’ü seçerek oluşturalım ve bu doğru parçasını $q_1$ olarak adlandıralım. $k$ doğrusunda yer alan $+1$ noktasından $r$ paralel doğru parçasını çizdiğimizde $\frac{-1}{+3}$‘ün konumunu elde edip sayı doğrusunda yerini $\frac{-1}{3}$ ile gösterebiliriz. Benzer şekilde $k$ doğrusunda $-3$, $d$ doğrusundan $+1$ noktasını birleştirdiğimizde elde ettiğimiz $q_2$ doğru parçası üçgende benzerlik gereği $q_1$ doğru parçasına ve $r$ doğru parçasına paralel olur. Bu durumda $\frac{+1}{-3}$ rasyonel sayısının $\frac{-1}{+3}$ rasyonel sayısına paralellik bağıntısı gereği denk ve sayı doğrusunda konumunun $\frac{-1}{3}$ olduğunu söyleyebiliriz. Böylece $\frac{-1}{+3}$ ve $\frac{+1}{-3}$‘ün sayı doğrusunda aynı konuma karşılık geldiğini yani birbirine denk olduğunu göstermiş oluruz.
İlkokuldan itibaren sorulan sorulardan birçoğunda, kesir gösterimlerinde paydada sıfırın olmaması farklı şekillerde anlatılmaya çalışılır. Bir kesrin paydasının neden sıfır olamayacağı, matematiksel olarak anlamlandırılması, incelemesi ve farklı öğrenci gruplarına aktarım açısından düşündüğünüzde aslında kolay bir kavram da değildir. Matematikçilerin “tanımsız” kavramı bu durumu karşılasa da çocuklar ve gençler bunu tanımsızlık olarak anlamlandırmakta oldukça zorlanırlar. Bu “tanımsızlık” durumunu farklı bir yolla anlamlandırabilir miyiz?
Yukarıda paralel doğrularla rasyonel sayıları sayı doğrusuna nasıl yerleştirebileceğimizi gösterdik. Benzer yöntemle, $0$ ve $3$ tamsayı olduğuna göre “$\frac{3}{0}$ sayı doğrusuna yerleştirilebilir mi?” problemini inceleyelim.
Problem 3: $\frac{3}{0}$’ın sayı doğrusunda bir konumu var mıdır?
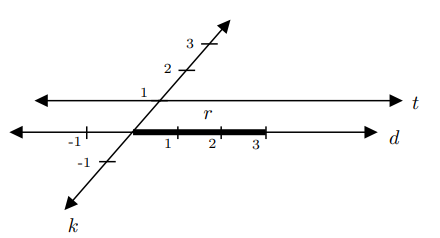
Yine aynı yöntemle $d$ doğrusundan +3, $k$ doğrusundan 0 sayısını aldığımızda oluşturduğumuz $r$ doğru parçasına Şekil-6’da olduğu gibi referans noktasından paralel çizelim ve $t$ ile adlandıralım.
$t$ doğrusu $r$’ye dolayısıyla $d$’ye paralel olduğundan hiçbir zaman $d$ doğrusunu kesmeyecektir. Bu durum bize $\frac{3}{0}$ sayısının sayı doğrusunda bir noktaya karşılık gelmediğini ve sonuç olarak $\frac{3}{0}$’ın reel sayı doğrusu üzerinde bulunmadığını yani bir reel sayı olmadığını da gösterir.
Siz de bu yöntemi kullanarak rasyonel sayılara ilişkin sıralama, çarpma ve bölme işlemlerinin sonuçlarını cebirsel işlemleri gerçekleştirmeden konumlarını elde ederek bulabilir misiniz? (İpucu: Çarpma işlemi ve bölme işlemi için rasyonel sayıları farklı sayı doğrularına yerleştirerek üçgende benzerliği düşünebilirsiniz.)
Kaynakça
- Matematik Dünyası Fonksiyon Özel Sayısı (2003-I). Türk Matematik Derneği, İstanbul.
- Karabey, B. (2019). Where is 1/3?: Constructing rational numbers on the number line by using parallel lines. Australian Mathematics Education Journal, 1(4), 27–33. https://search.informit.org/doi/10.3316/informit.837-706826177081

