Yazar: Hüseyin Demir (ODTÜ Emekli Öğretim Üyesi)

Yıl: 1995-1

Sayı: 21

1840 yılında C.L. Lehmus adında bir matematikçi büyük geometrici Jakob Steiner’e ilk bakışta basit görünen bir geometri problemi gönderir. Steiner, bu masum görünüşlü fakat zor problemi ileri geometri yöntemleri kullanarak çözer. O günden sonra bir çok matematik meraklısı bu probleme basit bir çözüm bulmaya uğraşmış ve söz konusu netice, biri matematiğe yaptığı büyük katkılarıyla herkesçe maruf, diğeri ise hiç tanınmamış iki matematikçinin adları yani “Steiner-Lehmus Teoremi” olarak şöhret kazanmıştır. [1, s.14]

Teoremin ifadesi şudur: İki iç açıortayı uzunlukça eşit olan bir üçgen ikizkenardır. Bu, ispatı çok kolay olan bir teoremin karşıtıdır. İspatı yönünde bir çok teşebbüs başarısız kalmışsa da, 1840 yılından bu yana teoremin 60 kadar başarılı ispatı verilmiştir. Lise kitaplarımızda yer almayan bu önemli teoremin eldeki bazı dergi ve kitaplardan derlenen dört ispatını burada okuyucularımza sunmak istiyoruz. Bunlardan ilk ikisi doğrudan, öteki ikisi dolaylı olup “olmayana eğri” yöntemine dayalı bulunmaktadır.

Bir $ABC$ üçgeninde $A$, $B$, $C$, köşelerinin karşısında kalan kenarların uzunluklarını sırasıyla $a$, $b$, $c$ ile, çevre uzunluğunu $2s$ ile, $A$, $B$, ve $C$ köşelerinden geçen iç açıortaylarının uzunlukları $n_a$, $n_b$, ve $n_c$ ile ve $\angle BAC$, $\angle CBA$, $\angle ACB$ açılarının ölçülerini de $2\alpha$, $2 \beta$, $2\gamma$ ile gösterelim.

İspat 1 (Doğrudan). Bilinen

$$ n_a = \frac{2}{a+b} \sqrt{bcs (s-a)}$$

$$ n_b = \frac{2}{c+a} \sqrt{cas (s-b)}$$

$$ n_c = \frac{2}{a+b} \sqrt{abs (s-c)}$$

formülleri kullanıldığında, $n_b = n_c$ varsayımından kolaylıkla $n_b^2 = n_c^2$ ve $n_b^2 – n_c^2 = 0$ yani

$$
(a+c)^2 b(s-c)-(a+b)^2 c(s-b)=0
$$
elde edilebilir: $2 s=a+b+c$ kullanılmak üzere bu denklemin her terimi 2 ile çarpılıp ifade $a$ nın kuvvetlerine göre düzenlendiğinde
$$
(b-c)\left[a^3+(b+c) a^2+3 b c a+b c(b+c)\right]=0
$$
bulunur ki köşeli parantez içindeki ifade, bütün terimleri artı olduğundan, sıfırdan farklıdır. O halde, $b-c=0$ olup üçgen ikizkenardır.

Not. Liselerde açıortay uzunlukları için yukarda verilen formüller elde edildiğinde, bir uygulama olarak bu teoremden söz etmeli ve öğrencilerden teoremin ispatı istenmelidir.

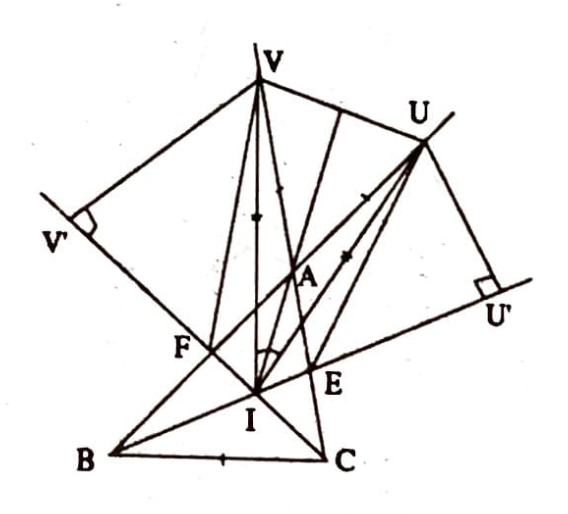
İspat 2 (Doğrudan, [4].) $A B$ ve $A C$ kenarları üzerinde $B E, C F$ sırasıyla $B$ ve $C$ den geçen içaçıortaylar olacak şekilde $E$ ve $F$ noktaları alalım. $B$ ve $C$ den geçen içaçıortayların uzunlukça eşit olduğunu yani $|B E|=|C F|$ olduğunu farz edelim. $B E$ ve $C F$ bir $I$ noktasında kesişsin (Şekil 1).

$A$ köşesi $U$ ve $B$, $C$ ve $V$ arasında kalacak ve $|A U|=|A V|=|B C|$ olacak şekilde $U$ ve $V$ noktalarını alıp ikizkenar $A U V$ üçgenini çizelim. $[U V]$ ‘nin orta dikmesi $I$ noktasından geçeceğinden (neden?) $|I U|=|I V|$ ve $|\angle A I U|= |\angle A I V |$ olacaktır.

Sırasıyla $U$ ve $V$ nin $B E$ ve $C F$ üzerindeki dikme ayaklarını $U^{\prime}$ ve $V^{\prime}$ ile gösterelim. $E B C$ ile $E U A$ üçgenlerinin alanları, bu üçgenlere ait $[B C]$, $[A U]$ kenarları ile bunlara karşlık gelen yükseklikler uzunlukça eşit oldug̃undan, (açıortay üzerindeki $E$ noktası $B C$ ve $A B$ doğrularından aynı uzaklıktadır !) eşittir. Bu alanlara $A B E$ üçgeninin de alanının eklenmesiyle $A B C$ ve $E U B$ üçgenlerinin, benzer olarak da $A B C$ ve $F V C$ üçgenlerinin, bu suretle de $E B U$ ve $F C V$ üçgenlerinin alanca eşit oldukları görülür. Bu üçgenlerde $[B E]$ ve $[C F]$ kenarları eşit olduğundan ilgili yüksekliklerin yani $\left[U U^{\prime}\right]$ ve $\left[V V^{\prime}\right]$ nin uzunlukça eşit oldug̃u görülür. Demek ki $U I U^{\prime}$ ve $V I V^{\prime}$ dik üçgenleri eşit olup
$$
\left|\angle U I U^{\prime}\right|=\left|\angle V I V^{\prime}\right|
$$
ve
$$
\left|\angle A I U^{\prime}\right|=\left|\angle A I V^{\prime}\right|
$$
ve en nihayet bir kaç basit işlemle
$$
\angle C B A=\angle A C B
$$
olduğu görülür.

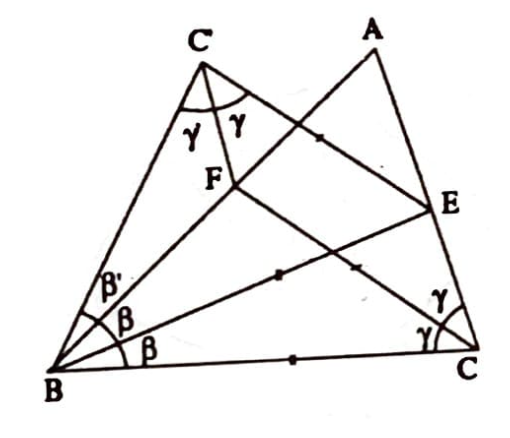
İspat 3 (Dolaylı, [3, s. 65-66].) $A B$ ve $A C$ kenarları üzerinde $B E, C F$ sırasıyla $B$ ve $C$ den geçen açıortaylar olacak şekilde $E$ ve $F$ noktaları alalım. (Sekil 2). $|B E|=|C F|$ ve $\beta<\gamma$ oldug̃unu kabul ederek bir çelişkiye varacag̃ız.

$E B C$ ve $F B C$ üçgenlerinde $|B E|=|C F|$ eşliğinden, ve $\beta<\gamma$ eşsizliğinden $|C E|<|B F|$ elde edilir.

$C E C^{\prime} F$ paralelkenar olacak şekilde bir $C^{\prime}$ noktası ithal edildiğinde, $|B E|=|C F|=\left|E C^{\prime}\right|$ olup $E C^{\prime} B$ üçgeni ikizkenardır. O halde, $\beta^{\prime}= \left | \angle FBC^\prime \right |$ ve $\gamma^{\prime} = \left | \angle BC^\prime F \right |$ yazarak, $\beta + \beta^\prime = \gamma + \gamma^\prime$ bulunur ki $\beta < \gamma$’dan $\beta^\prime > \gamma^\prime$ eşitsizliğini ve bundan da $FC^\prime B$ üçgeninde $|FC^\prime| > |FB|$ ve $|FC^\prime| = |CE|$ nedeniyle $|CE|> |FB|$ bulunur ki bu imkansızdır. Öyle ise, $\beta < \gamma$ olamaz. Benzer olarak $\gamma < \beta$ da olamaz. O halde, $\beta = \gamma$ olup üçgen ikizkenardır.

İspat 4 (Dolaylı). Bu ispat aşağıdaki yardımcı teoreme dayanmaktadır.

Yardımcı Teorem: Bir üçgende iki açıdan, ölçüsü daha küçük olana ait iç açıortayın uzunluğu, ölçüsü daha büyük olana ait iç açıortayın uzunluğundan daha büyüktür.

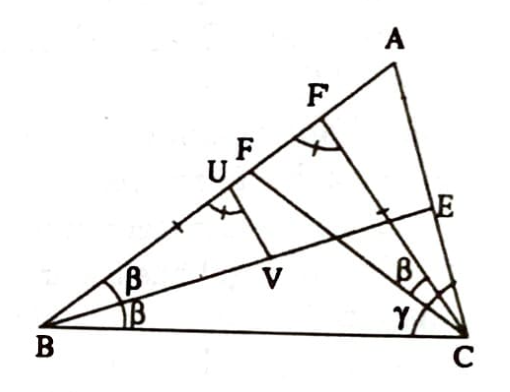
İspat ([2, s. 470]) $ \beta < \gamma$ olduğunu varsayalım. $A$ ve $F$ arasinda kalacak ve $\left|F^{\prime} C F\right|=\beta$ olacak şekilde bir $F^{\prime}$ noktası alalım (Şekil 3).

$F^{\prime} B C$ üçgeninde $\beta+\beta<\gamma+\beta$ oldug̃u için $\left|C F^{\prime}\right|<\left|B F^{\prime}\right|$ olup $B$ ve $F^{\prime}$ arasinda kalacak ve $|B U|=\left|C F^{\prime}\right|$ olacak şekilde bir $U$ noktası alınabilir. $B E$ dog̃rusu üzerinde, $U V || F^{\prime} C$ olmak üzere $V$ noktası alınacak olursa $\angle BUV = \angle BF^\prime C$ olup $U B V$ ve $F^{\prime} C F$ üçgenleri eşit olup, $|B V|=|C F|$ olmalıdır. $U V || F^{\prime} C$ olduğundan, $V$ noktası $B$ ve $E$ arasında kalır ve $|C F|=|B V|<|B E|$ elde edilir.

Bu yardımcı teoremi kullanarak, Steiner Lehmus teoremini dolaylı olarak şu şekilde (‘olmayana ergi’ ile) ispatlayabiliriz. Eğner $\beta<\gamma$ olsaydı, yardımcı teorem gereğince $n_b>n_c$ olurdu ki bu, $n_b=n_c$ varsayımıla çelişme yaratır. O halde $\beta<\gamma$ ve benzer olarak $\gamma<\beta$ olamaz, yani $\beta = \gamma$’dir

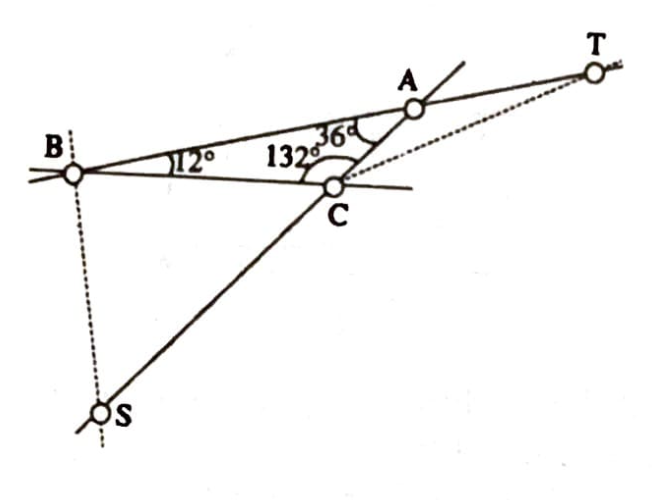
Yazımızı şu uyarı ile kapatıyoruz: Steiner-Lehmus teoremi üçgenin dış açıortayları için muteber değildir; yani ikizkenar olmayan bir üçgende iki dış açıortay uzunlukça eşit olabilir. Şekil 4 de bunun güzel bir örneğini teşkil eden ve ‘Bottema üçgeni’ olarak anılan üçgeni veriyoruz. [3, s.66]. $B$ ve $C$ köşelerine ait dış açıortayların bu üçgende uzunlukça eşit olduklarının ispatını okuyucularımıza bırakıyoruz.

Kaynaklar

[1] Coxeter, H. M. S., Greitzer, S.L., Geometry Revisited, New Mathematical Library, Vol. 19, 1967, New York and the L.W. Singer Co., Syracuse.
[2] Coxeter, H.M.S., Introduction to Geometry, John Wiley, New York, 1961.
[3] Court, N.A., College Geometry, Barnes and Noble, 1952, New York.
[4] J. V. Malesevic: “A direct proof of the Steiner-Lehmus teorem” Mathematics Magazine, 43(1970)101-107.

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Atahan Haznedar‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.